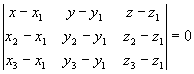
Univerza v Ljubljani
Fakulteta za strojništvo
A Straight Line and a Plane in 3D world
(Interactive Presentation of Intersection of Straight Line and Plane In 4-Parameter Viewing System)
1. september, 1999
Uvod | Teoretične osnove | Določitev točk | Struktura programa | Zaključek | Literatura
Abstract
This document presents using a simple viewing pipeline to show a plane and a straight line in 3D space. A simple 4-parameter viewing system and perspective projection are used to draw a wireframe objects (plane and line) on 2D screen coordinates. The plane and the line are defined by user defining either 1 point and a normal vector or 3 points, for the plane, and 1 point and s or 2 points, for the line. In this pape you can also find a hidden line detection algorithm which is not completely general but somehow specific for this case. A simple program and complete code written in Delphi are included.
V poročilu so prikazane metode in algoritmi za prikaz premice in ravnine v 3D prostoru. Uporabljena sta enostavni 4-parametrični sistem pogleda in perspektivna projekcija, s pomočjo katerih program na zaslon (2D koordinate) v žični obliki izriše kvadrat (kot del ravnine) in daljico (kot del premice). Premica in ravnina sta podani interaktivno (premica - 2 točki ali točka in smerni vektor; ravnina - 3 točke ali točka in normala na ravnino). Nevidni del premice za ravnino, se razlikuje od vidnega dela pred ravnino, kar je izvedeno s specifičnim (za konkretni primer) narejenim algoritmom.
Tako premico kot ravnino lahko podajamo v komponentni ali vektorski obliki, zaradi kasnejšega pretvarjanja v programsko kodo, pa sledenjega ne bomo potrebovali. Ravnino, podano z normalo n = (a,b,c) in točko T (x1,y1,z1), lahko zapišemo v komponentni obliki
a(x-x1) + b(y-y1) + c(z-z1) = 0,
ko pa je ravnina podana s tremi točkami pa je mešani produkt treh vektorjev na ravnini enak nič in velja
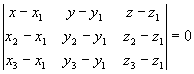
Premico podano s točko T (x1,y1,z1) in smernim vektorjem s = (l,m,n) zapišemo v komponentni obliki sledeče
![]()
Ko pa sta podani 2 točki, pa dobimo enako obliko kot zgoraj, le da so komponente smernega vektorja tokrat določene z razliko komponent obeh točk, kot lahko vidimo v spodnji enačbi
![]()
Prebod ravnine in premice lahko izračunamo na več načinov, najbolj ugoden način izračuna preboda pa je ta, da ravnino zapišemo v splošni obliki, premico pa v odsekovni obliki (glej zgornja dva izraza). Ravnino v splošni obliki podamo na način
Ax + By + Cz + D = 0,
kjer so posamezni parametri v primeru, da je ravnina podana s točko in normalo enaki
A = a B = b C = c D = (-ax1 - by1 - cz1),
ko pa je le-ta podana s 3 točkami, pa vse 4 parametre določimo na podlagi izraza, kjer je determinanta enaka nič. Če to determinanto izpišemo ter izpostavimo x,y in z, potem dobimo posamezne vrenosti parametrov izražene na naslednji način
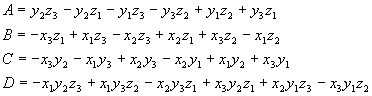
Koordinate preboda potem izračunamo dokaj enostavno
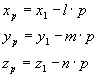 ,
,
pri čemer je faktor p enak
![]()
Zgoraj definirana smerni vektor in normala nista enotska.
Vse točke objektov v prostoru je potrebno nekako prikazati na 2D zaslonu tako, da je tretja dimenzija še vedno razvidna iz prikazane scene, kar storimo s posebno transformacijo točk od svetovnih (world) pa vse do zaslonskih (screen) koordinat. To se izvede z nekakšno simulacijo postavitve kamere v prostoru, hkrati pa podamo ustrezne parametre kamere, na podlagi česar se potem, s pripadajočo transformacijo, točke ustrezno projecirajo na neko ravnino, ki je v splošnem lahko tudi zaslon.
Kot je že omenjeno v uvodu, je tu za izris premice in ravnine uporabljena enostavna transformacija, t.j. poenostavitev splošne transformacije objektov iz 3D prostora na 2D zaslon. Pomeni, da uporabimo enostavni pogledni sistem (kaj to je, je razvidno v nadaljevanju). Prva poenostavitev je izbira nespremenljivega fokusa, ki je v tem primeru stalno v izhodišču svetovnega sistema, druga poenostavitev je ta, da kamere ni moč rotirati okrog njene osi, tretja poenostavitev pa je ta, da ne uporabljamo vidnega prostora (view volume) in rezanja (clipping) objektov glede na vidni prostor oz. zorni kot kamere. Ta zadnja operacija je pomembna, ko sta pozicija in orientacija kamere poljubni in se morajo v takem primeru deli objektov, ki niso v zornem kotu kamere, ustrezno odstraniti, v nasprotnem primeru namreč pride do nepravilnega izrisa objektov na zaslon (npr. knjižnica PHIGS uporablja splošni pogledni sistem).
Tudi tokrat bo možnost gledanja le dela objekta, tako imenovano rezanje pa bo izvedeno samodejno (negativne koordinate na zaslonu se bodo upoštevale, prikazane pa ne bodo - omejitev bo le max oz. min število koordinate ± 32767 oz. zorni kot kamere, ki bo tak, da rezanje ne bo potrebno). V nadaljevanju so prikazani posamezni koraki celotne transformacije iz 3D prostora na 2D zaslonske koordinate, za primer enostavnega, 4-parametričnega sistema gledanja.
Spodaj je prikazan način gledanja v 4-parametričnem sistemu gledanja in podajanje projekcijske ravnine, na katero se projecirajo posamezne točke, glede na pozicijo kamere. Prikazana je tudi pripadajoča transformacijska matrika Tview, ki transformira točke iz realnega 3D sistema (world coordinates), v pogledni koordinatni sistem - view coordinates - s kamero v izhodišču, koordinta zv pa je usmerjena proti izhodišču realnega (world) sistema. Pri tem so f,q, r in d parametri pravkar omenjenega sistema, ki jih lahko poljubno spreminjamo, kot rezultat pa dobimo različne slike scene na zaslon oz. projekcijski ravnini. Tokrat bo razdalja projekcijske ravnine d od kamere konstantna in bomo spreminjali le prve tri parametre. Kot smo že omenili, je pri tej vrsti poglednega sistema fokus (hkrati tudi smer zv) vedno v izhodišču realnega koordinatnega sistema, kar predstavlja določeno omejitev pri opazovanju predmetov - pomeni, da usmerjenost kamere ni splošna ampak je odvisna od njene splošne pozicije v prostoru.
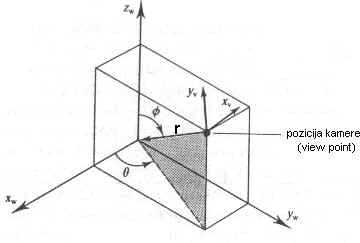
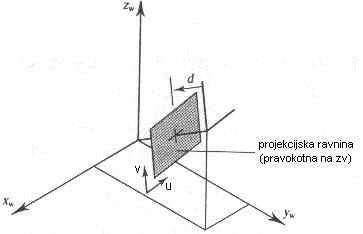
Sl. 1 4-parametrični sistem gledanja in postavite projekcijske ravnine
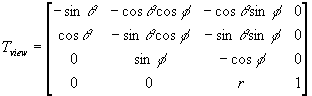
Če sedaj izrazimo poljubno točko svetovnega sistema (xw, yw, zw) v poglednem (view) koordinatnem sistemu, so njene koordinate v novem, poglednem (view) sistemu enake
![]()
Točka (xv, yv, zv) je še vedno na istem mestu v prostoru, le njene koordinate so napisane glede na kamero, s fokusom, kot ga prikazuje zgornja slika. Ko vpeljemo še perspektivno projekcijo, se posamezne točke ustrezno projecirajo na projekcijsko ravnino (u,v koordinati) in sicer se koordinati xv in yv spremenita za faktor d/zv (za konkretni primer, ko je fokus v izhodišču realnega sistema, zv pa je v smeri normale proj. ravnine), koordinata zv pa ostane nespremenjena. Z d je označena razdalja od kamere do proj. ravnine, na podlagi podobnostnih trikotnikov (glej spodnjo sliko) pa dobimo naslednji zvezi
![]()
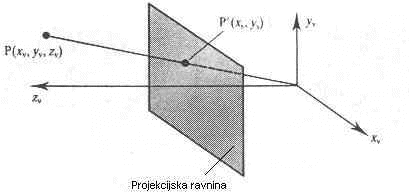
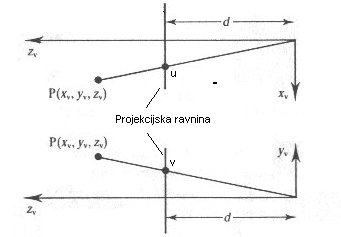
Sl. 2 Projeciranje poljubne točke P v poglednem sistemu (view) na projekcijsko ravnino (u,v) pri perspektivni projekciji
Sledi le še pretvorba na zaslonske (xs ,ys) 2D koordinate (tako imenovani mapping) in sicer glede na izbrano velikost okna (view window), ki ga definiramo na projecirni ravnini (v tem primeru postavljen vedno simetričeno na izhodišče u,v sistema), dimenzij AwxAw ter izbrano velikost okna na zaslonu (viewport), dimenzij WxH. To bi lahko imenovali tudi skaliranje v 2D na podano velikost okna na zaslonu..
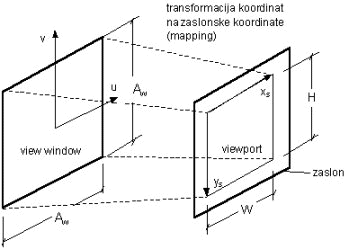
Sl. 3 Window to viewport transformacija
Če naj bo koordinatno izhodišče na središču zaslonskega okna, potem je transformacija iz vidnega okna (view window) na zaslonske koordinate (viewport) naslednje oblike

Vse zgoraj napisano je potrebno le še ustrezno preliti v programsko kodo, v posamezne podprograme, ki bodo posamezne točke ustrezno transformirali. V našem primeru sta namreč ravnina in premica sestavljeni iz posameznih točk, te pa so medseboj ustrezno povezane z ravnimi črtami (tako imenovana žična predstavitev objektov). Tako, da se transformirajo le točke, ki jih potem na zaslonu le medsebojno ustrezno povežemo.
Da lahko izvedemo zgoraj predstavljeno transformacijo na konkretnih objektih, je potrebno določiti točke teh objektov (ravnina, premica in koordinatni sistem) v prostoru, torej v svetovnih (world) koordinatah (xw,yw,zw). Te točke se potem preko zgoraj omenjenih transformacij ustrezno preslikajo na 2D zaslon, kjer jih le še ustrezno medsebojno povežemo s črtami. Izjema je le premica, ki jo je potrebno izrisati po delih (nevidni in vidni deli), glede na to ali je premica pod ali nad ravnino, kar pa je odvisno tudi od pozicije kamere. Ta zadnji del je izveden v podprogramu DrawScene, kjer se nevidni in vidni del premice določita na podlagi že znanih T5 in T9 (krajišči daljice, ki predstavlja premico) oz. je algoritem v grobi verbalni obliki predstavljen v nadaljevanju.
Tako premica kot ravnina imata neskončno razsežnost, na zaslonu pa lahko prikažemo le del premice in ravnine. Najbolj smiselno je tokrat prikazati nek del ravnine in premice okrog preboda, če le-ta obstaja, v nasprotnem primeru prikažemo poljuben odsek premice in ravnine. Najbolj enostavno je predstaviti ravnino s kvadratom končne velikosti, ki leži na tej ravnini, in premico končne dolžine v okolici prikazanega kvadrata. Tokrat se odločimo za spodaj prikazano razporeditev točk, ki pripadajo premici in ravnini, vse pa pa imajo tri komponente (x, y in z). Na spodnji sliki so prikazane tudi točke, ki pripadajo koordinatnemu sistemu v prostoru.
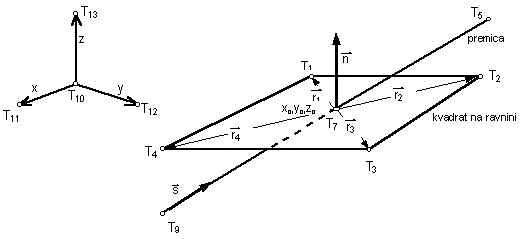
Sl. 4 Določitev točk premice, ravnine in koordinatnega sistema v prostoru
Definicija vektorjev r1 do r4 je potrebna zaradi izrisa kvadrata na način, kjer se najprej določi poljubna točka na ravnini, na podlagi tega se določi vektor r1 razdalje R (velikost polovične diagonale kvadrata in polovična dolžina daljice, ki predstavlja premico - glej programsko kodo), s pomočjo vektorskega produkta pa se določijo še vektorji r2 do r4 in hkrati točke T1 do T4.
V primeru, da sta premica in ravnina vzporedni, izrišemo poljuben odsek premice in ravnine.
Vse točke in njihova določitev so podrobneje razvidni iz podprograma Points.
Zaradi lažje 3D predstave ravnine v prostoru, se lahko izrišejo dodatne vzporednice na ravnini, ki tvorijo mrežo oz. šahovnico, ker le-ta izboljša predstavo o tretji razsežnosti. Definicija teh točk je prav tako podana v podprogramu Points.
Sl.5 Izgled ravnine z dodatnimi vzporednicami pri opazovanju s perspektivno projekscijo
Nevidni del premice določamo na u,v koordinatah, torej na projekcijski ravnini, in sicer na podlagi prekrivanja premice s kvadratom. Začetek in konec prekrivanja v splošnem določata izračunana preseka P1 in P2, izračunamo pa jih na podlagi znanih točk premice in ravnine. Presek P1= (u,v) na spodnji sliki bi izračunali sledeče
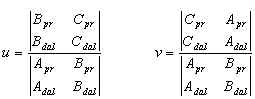 ,
,
pri čemer dal označuje daljico od 1 do 2, pr premico, posamezni členi determinant pa so oblike
![]()
Naslednji korak je določitev vidnosti premice na mestu prekrivanja, t.j. ali je premica na mestih prekrivanja P1 in P2 pod ali nad ravnino. To določimo na podlagi izračuna zv koordinate tako za premico kot za daljico kvadrata na mestu prekrivanja Pi. Iz sl.2 lahko na podlagi yv-zv projekcije zapišemo izračun zv koordinate za premico (podobno je za daljico), ker poznamo v (y koordinata preseka na proj. ravnini) in tudi view koordinate premice (Tv5 in Tv5). To pomeni, da moramo na podlagi znanih krajišč premice v view koordinatah (3 komponente) in znanih koordinatah točke prekrivanja (u,v) na projekcijski ravnini, določiti view koordinato v z smeri, ki pripada temu preseku. To storimo tako za premico, kot za daljico kvadrata, ki seka premico na projekcijski ravnini. Primer izračuna za premico je
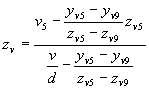
Ko izračunamo zv za premico in daljico, ki se sekata na proj. ravnini, določimo vidnost premice na mestu začetka ali konca prekrivanja Pi.Premica je na tem mestu vidna, če je njen zvmanjši od zv, ki pripada daljici kvadrata. Na podlagi tega se sestavi ustrezen algoritem za določitev vidnosti posameznih odsekov premicein sledi le še izris premice od Ts5 preko P1, P2, morebitnega preboda Ts7 in vse do Ts9, pri čemer je nevidni del premice izrisan črtkano. Seveda pa je pri tem potrebno upoštevati možnosti, da je lahko npr. razdalja T5T9 krajša kot razdalja P1P2 in podobno. Algoritem določevanja nevidnega in vidnega dela premice je razviden iz podprograma DrawScene.
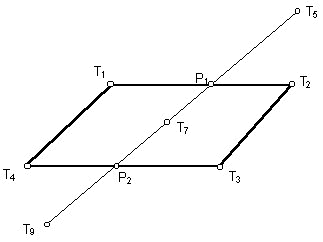
Sl. 6 Določanje nevidnega dela premice na projekcijskih koordinatah s pomočjo presekov P1 in P2
Zgoraj omenjene točke so naslednje: Tv(xv, yv, zv) so točke v view koordinatah, T (u,v) so točke na projekcijski ravnini, Ts(xs, ys) pa točke na zaslonskih koordinatah. Vse te točke pa dobimo s posameznimi transformacijami točke v svetovnih koordinatah Tw(xwywzw).
Na spodnji sliki je prikazana blokovna shema poenostavljene transformacije oz. postopek od podajanja točk, pa do izrisa na zaslonu. Kot je bilo že omenjeno, ta transformacija ne vsebuje definicije vidnega prostora in rezanja, kot to vsebuje splošni pogledni sistem (npr. tisti v PHIGS), temveč ima program določeno omejitev, na podlagi katere rezanja ni potrebno izvesti: kamera je lahko le na takšni poziciji, kjer nobena točka scene ni za kamero (zv koordinata vsake točke je večja ali kvečjemu enaka nič).
Program je v bistvu aplikacija z vnosnimi polji in gumbi, s katerimi ineraktivno spreminjamo parametre ravnine, premice in kamere. Vsaka sprememba se odraža v drugačnem izrisu scene na zaslonu, tako da dobimo občutek, kot da opazujemo sceno nekje v prostoru, kar predstavlja trenutna pozicija kamere (view point).
Kot je razvidno iz spodnje sheme, podprogram ViewScene združuje vse transformacije (v njem se transformirajo vse točke) in je sestavljen iz podprogramov Tview (transformacija točk na pogledne - view - koordinate), Tuv (transformacija točk na projecirno ravnino ob izbrani perspektivni projekciji) in Map (transformacija točk na zaslonske koordinate). Samostojna enota je podprogram DrawScene, ki pa vsebuje tudi algoritem za izris premice po delih (vidni in nevidni deli).
Poleg omenjenih, sta definicija in celotna povezava tudi ostalih podprogramov, razvidna v celotni programski kodi.
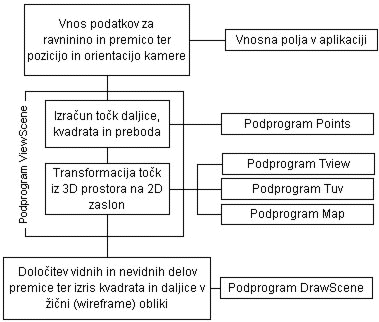
Sl. 7 Blokovna shema zgradbe programa in hkrati tudi potek enostavne transformacije za 4-parametrični pogledni sistem
Spodaj je prikazano glavno okno programa z vnosnimi polji, in gumbi za interaktivno podajanje premice in ravnine ter spreminjanje pozicije kamere.
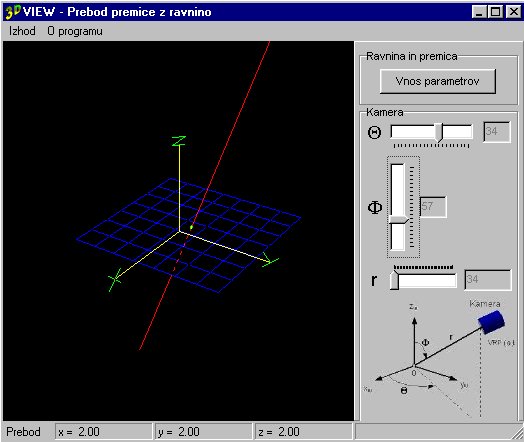
Sl. 8 Izgled aplikacije 3D view
Za dodatno pojasnitev posameznih algoritmov, si lahko ogledate celotno kodo programa vključno z aplikacijo ali samo končno aplikacijo. Program je napisan v jeziku Object Pascal v razvojnem okolju Delphi.
Ker je bilo bistvo pri tej nalogi prikazati interakcijo med premico in ravnino (poleg koordinatnega sistema edina objekta), je bila izbira enostavnega 4-parametričnega sistema pogleda zadovoljiva. Prav tako pa smo z omejitvijo pozicije kamere, ta je taka, da so vsi objekti v njenem zornem kotu, odpravili definiranje poglednega prostora in rezanje glede na ta prostor (to potrebujemo v splošnejših primerih, kjer je npr. predmet za kamero ali pravokotno na smer gledanja). Uporaba uporabljenega sistema torej zadosti namenu prikazati premike kamere v prostoru in glede na njeno pozicijo prikazati 3D objekte, postavljene v prostoru, na 2D zaslonu. V primeru splošnejše uporabe poglednega sistema, pa bi bilo potrebno uporabiti vsaj 8-parametrični ali celo splošni pogledni sistem, kjer je potrebno, poleg večjega števila parametrov, uvesti tudi tako imenovano rezanje (clipping) glede na definirani pogledni prostor (zorni kot kamere).
1. Watt, A., 3D Computer Graphics, Second Edition, Adison-Wesley, Wokigham, England, 1993
2. Bronštajn, Semendjajev, matematični priročnik, 2. izdaja, Tehniška založba Slovenije 1997