V 3D prostoru izrišite dve ravnini, ki ju lahko interaktivno določimo (tri točke ali točka in vektor normale na ravnino). Izračunajte premico preseka obeh ravnin in jo ustrezno označite v prikazu. Omogočeno naj bo naknadno spreminjanje kota pogleda na sceno, povečave in pomiki (3D transformacije).
Točke ravnine in ravnina sama je podana v world koordinatnem sistemu, katerega pa ni mogoče samodejno prenesti iz 3D zapisa v 2D obliko. V world koordinatnem sistemu nimamo podane točke, iz katere uporabnik opazuje model. Da bi model lahko prikazali na zaslonu je potrebno podati točko iz katere opazujemo objekt in v kateri smeri. Vsako točko, ki popisuje model v prostoru je potrebno transformirati v view koordinatni sistem.
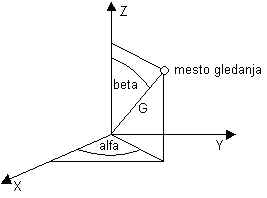
Poznamo več vrst view (vidnih) koordinatnih sistemov. V nalogi je uporabljen krogelni pogledni koordinatni sistem, kjer je potrebno podati mesto gledanja. Pogled opazovalca je vseskozi usmerjen v središče homogenega koordinatnega sistema. Mesto gledanja podamo z tremi parametri:
alfa: zasuk okrog Z osi v world koordinatnem sistemu
beta: kot med Z osjo in zveznico točke gledanja in izhodišča koordinatnega sistema
G: razdalja od koordinatnega izhodišča do točke gledanja

Da bi točke iz world koordinatnega sistema prenesli v view koordinatni sistem, moramo vsako točko posebej, ki popisuje objekt, množiti s transformacijsko matriko:
Tview =
| -sin(alfa) | -cos(alfa)cos(beta) | -cos(alfa)sin(beta) | 0 |
| cos(alfa) | -sin(alfa)cos(beta) | -sin(alfa)sin(beta) | 0 |
| 0 | sin(beta) | -cos(beta) | 0 |
| 0 | 0 | G | 1 |
[Xv, Yv, Zv, 1] = [Xw, Yw, Zw, 1] * Tview
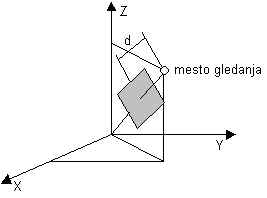
Dobili smo točke v view koordinatah, za prikaz modela pa je potrebno le tega projecirati na pogledno ravnino. Pogledna ravnina je postavljena pravokotno na Z - os view koordinatnega sistema in je za d oddaljena od njegovega izhodišča.
Točke podane v view koordinatnem sistemu sedaj množimo z matriko Tpers:
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1/d |
| 0 | 0 | 0 | 0 |
[Xp, Yp, Zp, 1] = [Xv, Yv, Zv, 1] * Tpers
Za projeciranje modela sta dovolj samo dve koordinati Xp in Yp. Z množenjem točk z opisanimi matrikami smo dobili zapis točk primeren za prikaz na zaslonu.
Točke, katere dobimo na zaslon se lahko pojavijo tudi izven vidnega polja. Da bi videli tudi robne točke, lahko premaknemo sliko na zaslonu s pomočjo matrike Tpr, kjer so:
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| X | Y | Z | 1 |
[Xg, Yg, Zg, 1] = [Xp, Yp, Zp, 1] * Tpr
V programu en pritisk na gumb za premik pomeni premaknitev modela v željeni smeri za 10 pikslov.
Program je napisan v programskem jeziku C++ za Windows okolje.Program deluje po sledečih korakih:
Program ima vgrajene še nekatere ukaze za lažje ogledovanje ravnin v prostoru:
Model je prikazan z različnimi barvami zaradi boljše ločljivosti. Narejen je le žični model.
Program je primeren za prikaz dveh ravnin v prostoru, ki se medsebojno sekata. Prikaže nam presečno premico. Vidimo lahko, v kateri smeri v prostoru se ravnini sekata in pod kakšnim kotom. Omogočen je pogled iz različnih zornih kotov in iz različne razdalje.
Download programa in izvorne kode