Univerza v Ljubljani, FAKULTETA ZA STROJNIšTVO, Računalniško podprto konstruiranje.
Avtor: Janko Slavič, mentor: Janez Krek.
Run program
Abstract / Povzetek,
Kratek princip delovanja,
Uporabniški vmesnik,
Zaključek,
Reference,
Dodatek - uporabljene funkcije
The essence of this project was to learn basic concepts of 3D data display.
To achieve this goal we used a simple Java PHIGS library (SIMPLE PHIGS v 0.0.2. Copyright 1998
LECAD)
in connection with JavaScript web page.
This program shows two planes in intersection. Planes can be defined with 2 x 3 points or 2 x (1 point + vector).
Povzetek
Namen programa je učenje osnovih operacij prikazovanja prostorskih objektov.
Naloge smo se lotili s pomočjo preproste Java PHIGS knjižnice (SIMPLE PHIGS v 0.0.2. Copyright 1998
LECAD), ki smo jo upravljali
s pomočjo skriptnega jezika - JavaScript.
Zajem podatkov
Program predvidi naslednja načina podajanja vhodnih podatkov:
- podajanje treh točk, ki nedvoumno definirajo ravnino
- podajanja točke in normalnega vektorja na ravnino
Po zagonu programa se najprej testirajo vhodni podatki (ali so točke
kolinearne, saj tedaj ne definirajo ravnine).
Sledi poenotenje podatkov v obliko točka + normirani normalni vektor
Nato se testira vzporednost ravnin, če sta ravnini vzporedni se izpiše opozorilo in program prekine
z izvajanjem.
Izračun presečiščne premice in sekajočih se ravnin
Na tem mestu se pojavi vprašanje, kje izrisati presečiščno premico in sekajoči se ravnini.
Izkaže se, da je najbolj praktično, da to storimo v okolici točke na premici, ki je
najbližja izhodišču (poimenujmo jo closest point).
Izračun "closest point-a"
Naj najprej definiramo nekatere oznake, ki jih bomo pozneje rabili:
Enačba ravnine je oblike:
A*x + B*y + C*z + D=0
(kjer je vektor (A,B,C) normirani normalni vektor na ravnino in
D oddaljenost ravnine od izhodišča)
 - normirani normalni vektor premice (dobimo ga z križnim vektorskim produktom normalnih vektorjev ravnin)
- normirani normalni vektor premice (dobimo ga z križnim vektorskim produktom normalnih vektorjev ravnin)
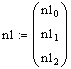 - normirani normalni vektor prve ravnine
- normirani normalni vektor prve ravnine
d1 - oddaljenost prve ravnine od izhodišča (parameter enačbe prve ravnine)
 - normirani normalni vektor druge ravnine
- normirani normalni vektor druge ravnine
d2 - oddaljenost druge ravnine od izhodišča (parameter enačbe druge ravnine)
Ker imamo dve ravnini, ki imata skupaj 3 spremenljivke, ostane ena spremenljivka nedoločena.
To nas ne moti, saj lahko to spremenljivko izenačimo s konstantno vrednostjo in potem izračunamo
vrednosti ostalih dveh spremenljivk.
Pojavi se torej vprašanje katero spremenljivko izenačimo s konstantno vrednostjo.
Na to vprašanje nam da odgovor normalni vektor premice:
-
Če je normalni vektor premice vzporeden z X osjo ali vzporeden z XY ravnino potem nekje
seka ravnino YZ in lahko spremenljivko x izenačimo s konstanto (x=0).
y in z izračunamo tako:

-
Če je normalni vektor premice vzporeden z Y osjo ali vzporeden z YZ ravnino potem nekje
seka ravnino ZX in lahko spremenljivko y izenačimo s konstanto (y=0).
z in x izračunamo tako:
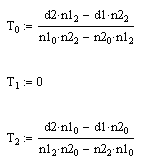
-
Če je normalni vektor premice vzporeden z Z osjo ali vzporeden z ZX ravnino potem nekje
seka ravnino XY in lahko spremenljivko z izenačimo s konstanto (z=0).
x in y izračunamo tako:
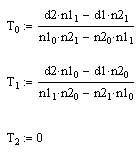
Sedaj smo torej izračunali poljubno točko na presečiščni premici:
Sledi izračun izhodišču najbližje točke.
Imamo naslednjo geometrijsko odvisnost:

Na naslednji sliki je označena (skalarna) razdalje med točkma T in S:

Na sliki vidimo, da je razdalja med t.i. najbližjo točko in t.i. poljubno točko enaka
vektorskemu produktu krajevnega vektorja in normiranega normalnega vektorja presečiščne premice.
Ko to razdaljo izračunamo, dobimo najbližjo točko na premici tako, da od krajevnega vektorja
vektorsko odštejemo normalni vektor premice pomnožen z razdaljo med točkama (razdalja, ki smo jo
izračunali zgoraj). To operacijo prikazuje naslednja slika:

Sledi izračun točk posamezne ravnine v okolici closest point-a. Ta izračun je
zaradi praktičnosti (da imamo vse objekte pri rotaciji v vidnem polju) odvisen od
razdalje med izhodiščem in closest point-om.
Transformacije
Sam princip transformacij je tak, da se vsaka posamezna 3D točka transformira glede na
zahtevo (imamo naslednje možnosti: translacija, skalacija in vrtenje okoli osi-vektorja).
Ker so standardne transformacijske matrike dobro znane in jih najdemo v vsaki knjigi, ki
obravnava tridimenzionalno grafiko, bom na tem mestu izpostavil samo
transformacijsko matriko za vrtenje okoli osi (vektorja):
Če je:
 enotni normalni vektor,
ki označuje os vrtneja,
enotni normalni vektor,
ki označuje os vrtneja,
in f kot vrtenja, potem lahko uporabimo matriko:
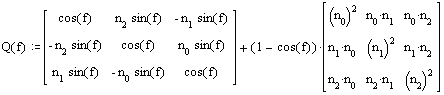
kot transformacijsko matriko za rotacijo okrog vektorske osi.
Za prikaz v 2D prostoru - ravnini zaslona sem uporabil navaden vzporeden pogled.
Sam uporabniški vmesnik bi naj bil čimbolj intuitiven.
In sicer na vrhu najprej vnesemo podatke, nato pa z odločitvenim gumbom izberemo
kateri tip vnosa (2x3point ali 2x(point+vector)) želimo prikazati. Zraven podatkov
za definiranje ravnine s tremi točkami lahko zahtevamo, da se izriše tudi trikotnik,
ki povezuje vhodne podatke.
Desno od prikazovalnega polja se nahaja nadzorna plošča.
Tako lahko najprej uporabimo gumba za povečanje in pomanjšanje (pod njima lahko
definiramo faktor skalacije).
Sledijo gumbi za premikanje vidnega polja.
In končno je tukaj še kontrola za vrtenje okoli lokalnega koordinatnega sistema.
In v skrajni desni legi so tukaj še gumbi za izbiro med nekaterimi standardnimi
pogledi ter potrditvena polja za prikaz posameznih objektov.
Preden sem se lotil izdelave pričujočega programa, JavaScripta nisem obvladal; sedaj lahko rečem,
da ga vsaj približno obvladam. Sicer pa sem se naučil predvsem tega, da je potrebno
funkcije narediti zelo splošno in jih na koncu dobro testirati. Pri izdelavi programa sem se
držal pravila, da se omejitve, funkcije definirajo samo enkrat, tako, da nobena
stvar ni definirana na dveh mestih.
Mislim, da sem s tem veliko prihranil na preglednosti in zmožnosti poprave.
Kakor prej nisem znal programirati v JS, si tudi prej niti predstavljal nisem kako bi programiral
grafični prikaz. Sedaj vem, da to za preprosto predstavitev niti ni tako zapleteno.
Pri tem sem se naučil, da mora biti zelo jasno izdelan sam koncept programa, pomemben je predvsem
redosled operacij. Sicer pa mislim, da sposobnost programa spoznamo predvsem v njegovi prožnosti. To prožnost programa sem
spoznal, ko sem brez večjih težav proti koncu programiranja naredil, da so posamezni objekti po želji vidni in da
se pogled prilagodi realnim dimenzijam (AutoScale).
Sicer pa mi je bilo glavno vodilo pri izdelavi programa, da je program preprost za uporabo in predvsem funkcionalen.
Upam, da mi je uspelo.
- Janez Vrhovec, Uvod v JavaScript - predavanja, 2000
- Mihael Perman, Matematika, ortogonalne preslikave - predavanja, 1998
- Uroš Mesojedec, JAVA - programiranje za Internet,1996
- Alan Watt, Fundamentals of Three-Dimensional Computer Graphics, 1989
Managing functions / Upravne funkcije
Run(start,transform_type,input_type,show_hide,direction)
Step in function
StartPHIGS()
Starting PHIGS
EndPHIGS()
Braking connection with PHIGS
Calculate()
Calculating new transformated points
Draw()
Drawing with PHIGS
Mathematical assistance functions / Pomožne matematične funkcije
Point3D(x,y,z)
Define a 3D point
Point3D_4 (point1,point2,point3)
Finding the fourth point of a rectangle
Length(a)
Calculating the length of a vector
VectorSum(a,b,sign)
Sumation of two vectors
VectorMultiply(num,b)
Multiply a vector
DotProduct(a,b)
Dot product of two vectors
CrossProduct(a,b)
Cross product of two vectors
NormalOnPlane(a,b,c)
Finding a normal vector on the plane of three points
Identiti4x4()
Identiti matrix 4x4
IntersectionPoint()
Finding the closest point (to the origin) on the intersection line of two planes
Transformation in 3D / Transformacija v prostoru
Translate(dx,dy,dz)
Translation matrix
Scale(sx,sy,sz)
Scale matrix
RotateAboutAxis(axis,angle)
Rotation matrix (around given axis)
Transform(point,transf_matrix)
Transformation matrix
Projection()
Viewing projection matrix (3D -> 2D)
Finding the boundaries of objects / Določitev mejnih točk objektov
TriangleBoundary(data)
Finding the triangle connecting the three input points
PlaneBoundary(normal)
Finding the four points around the intersection point (the closest point to origin) that are lying on a plane (with the center point and normal vector)
LineBoundary()
Finding the two points defining the intersection line
Getting data for 2D PHIGS / Priprava za izris s PHIGS (2D)
CSystem(data)
Building the coordinate system
Plane(data)
Building the plane
PlaneVector(data)
Building the normal vector on the plane
Triangle(data)
Building the triangle
Line(data)
Building the line
Servicing and testing data / Priprava in testiranje podatkov
GetPoint(point3dString)
Get 3D point from a string
TestZoomInput()
Testing the data from string input (data from form)
Number2String(number)
Converting the number to string
Collineariti(p1,p2,p3)
Testing the collineariti of three vectors
Janko Slavič, 13.5.2000.

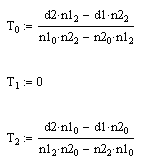
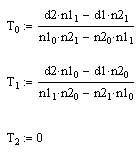
 - normirani normalni vektor premice (dobimo ga z križnim vektorskim produktom normalnih vektorjev ravnin)
- normirani normalni vektor premice (dobimo ga z križnim vektorskim produktom normalnih vektorjev ravnin)
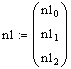 - normirani normalni vektor prve ravnine
- normirani normalni vektor prve ravnine
 - normirani normalni vektor druge ravnine
- normirani normalni vektor druge ravnine

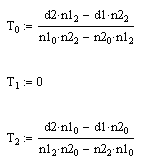
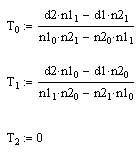



 enotni normalni vektor,
ki označuje os vrtneja,
enotni normalni vektor,
ki označuje os vrtneja,