Kazalo:
1. Abstract #
The Bezier patch is the surface extension of the Bezier curve. Whereas a curve is a function of one variable and takes a sequence of control points, the patch is a function of two variables with an array of control points. Bezier patch can be viewed as a continuous set of Bezier curves. The Bezier patch is the most commonly used surface representation in the computer graphic.The purpose of this task was to create a program, which draw two Bezier patches. Patches lies within the convex hull of its control points. Control points are defined by user. There must be 16 control point for each patch. Program enables changing the control points. Points can be changed in text area. Each control point is written in this way: [i j x y z], where i and j means the index of point and x, y and z coordinates of that point. Program enables the user to observe the patches under different positions and scales.
Program for drawing two Bezier patches
2. Definicija naloge #
Izdelajte program, ki dva zlepka prikaže kot žični model s poljubno homogeno transformacijo. Omogoča naj spreminjanje koordinat kontrolnih točk ( 2x16 točk) . Začetna postavitev kontrolnih točk naj bo taka, da je prehod iz enega zlepka na drugi zlepek zvezen. Program izdelajte s programskim jezikom JavaScript ( izris s pomočjo PHIGS knjižnice ).
3. Teoretične osnove #
Uvod
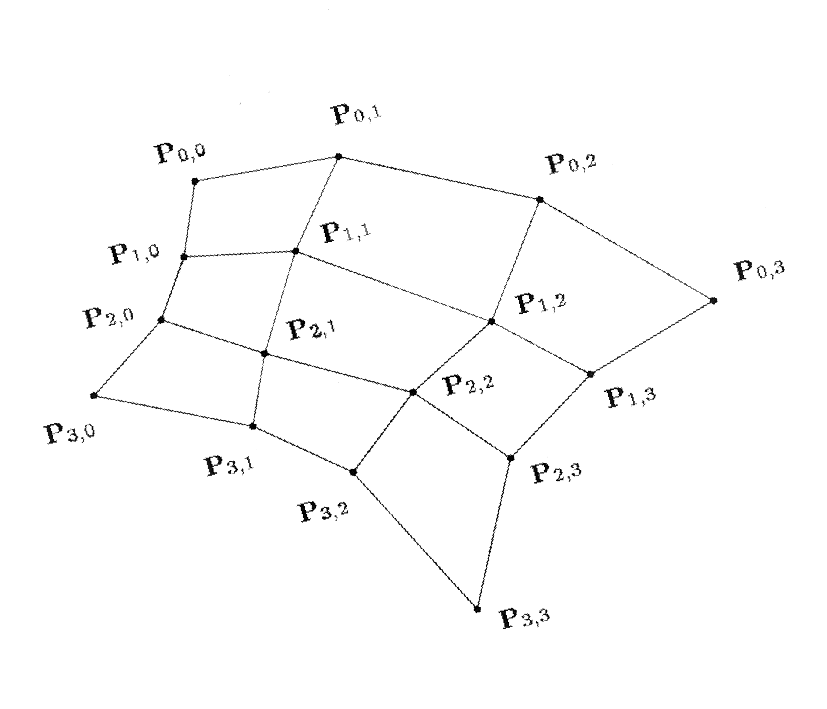
Pri oblikovanju glinenih modelov v vzorčni delavnici iz gline z šablonami ( prostorskimi krivuljami ) odvzemajo odvečni material. Sablona zareže v glino in nastala površina je ploskev. Tako lahko definiramo ploskev kot množico točk v prostoru, ki jih popiše prostorska krivulja, ko se giblje skozi prostor in pri tem spreminja svojo obliko. Predpostavimio, da se giblje po prostoru Bezierjeva krivulja. V vsakem trenutku je določena z množico kontrolnih točk. Bezierjeva površina je tako direktna razširitev Bezierjeve krivulje. Točka na površini je podana z dvo-parametrično funkcijo, ki je sestavljena iz povezovalnih funkcij za vsak parameter posebej. Pij so kontrolne točke, ki tvorijo polieder .
Definicija in matematični zapis Bezierjeve površine
Površina je podana z mariko n x m kontrolnih tock
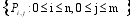 .
.
 .
.
Površina parametrizirana z dvema spremenljivkama je podana z enačbo :
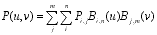
Bi,n(u)Bj,m(v) je produkt bi-variantnih Bernsteinovih polinomov.
Matrični zapis Bezier-jeve površine
Z matričnim zapisom enačbe površine dobimo obliko , ki je primerna za uporabo v računalniku. Za opis površine z matrikami 4x4 imamo na razpolago 16 kontrolnih točk. Tako je :

Parametra u in v zavzemata vrednosti od 0 do 1 .
Lastnosti Bezier-jeve površine
Lastnosti površine so podobne lastnostim Bezierjeve krivulje :
3.1. Opis programa za izris površine #
Program je napisan v JavaScriptu, izris je izveden z uporabo PHIGS knjižnice. Program prebere vhodne podatke ( polje kontrolnih točk ) in z uporabo matrične enačbe za Bezierjevo površino računa polje točk Bezierjeve ploskve ( preteče vse vrednosti parametrov U in V in za vsako vrednost izračuna točko na Bezierjevi ploskvi ). Tako z velikostjo parametrov U in V določamo število Bezierjevih točk oziroma gostoto Bezierjeve ploskve. Stevilo računskih operacij raste s produktom števil U in V, zato se pri večjih vrednostih parametrov program dalj časa izvaja.Izris
Za izris se izvedejo geometrijske transformacije nad kontrolnimi točkami ter koordinatnim sistemom. Točke Bezierjeve mreže se izračunajo iz transformiranih kontrolnih točk. Za izris 3D objekta na 2D ravnino potrebujemo 2 koordinati, v tem primeru se izrisujejo x in z koordinate Bezierjeve mreže. Program računa z zmnoženimi matrikami za rotacijo, skalacijo in translacijo.
Transformacijske matrike v 3D prostoru so sledeče oblike :
Rotacije
Okrog osi X: 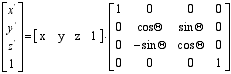
Okrog osi Y: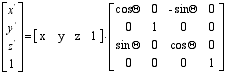
Okrog osi Z: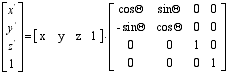
Translacija
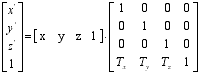
Skaliranje
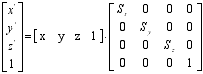
Transformacija točk se vrši z množenjem vektorja točke z transformacijsko matriko. Vektor točke je dimenzije 3x1, transformacijska matrika v 3D pa je velikosti 4x4. Produkt matrik, je mogoč le takrat, ko je število stolpcev leve matrike enako številu vrstic desne matrike. Da je množenje mogoče, se v vektor točke uvede še četrto koordinato, ki ima vrednost 1. Tako dobimo t.i. homogene koordinate, ki omogočajo množenje vektorja točke z transformacijsko matriko.
3.2. Program za izris površine #
Program prikaže dve Bezierjevi površini, kot žični model. Vsako površino določimo s 16 kontrolnimi točkami. Posamezna kontrolna točka ( i , j ) je določena z x, y in z koordinato. Koordinate kontrolnih točk zapišemo v tekstovnem polju za vsako površino posebej. Zapis je oblike [ i j x y z ], kjer sta i,j indeksa točke in x y z njene koordinate. Začetna postavitev kontrolnih točk je takšna, da je prehod iz ene v drugo površino zvezen.
Gostoto žičnega modela površine določimo z velikostjo števil U in V.
Program za določitev kontrolnih točk in izris površine
4. Zaključek #
Program omogoča nazorno predstavitev problema s katerim se je ukvarjal Pierre Bezier. Bezier je bil inženir Renaulta, ki se je v 60. letih ukvarjal s problemom, kako prototipno geometrijo avtomobilske karoserije ( katero so oblikovali npr. iz lesa ) prenesti na risalne deske, oziroma jo nedvoumno matematično določiti. Leta 1966 je v reviji Automatisme objavil članek, kjer je definiral 3D parametričen popis krivulj.
Bezierjeva površina je pogosta in osnovna predstavitev površine v računalniški grafiki, njeno razumevanje pa predstavlja temelj za razumevanje tega področja.
Pri izdelavi naloge sem se seznanil z osnovami jezika JavaScript ter izrisom z uporabo PHIGS knižnice. Pomembne pa so tudi 3D transformacije, ki omogočajo, da dobimo prostorsko predstavo o objektu.
5. Literatura #
1. Peter Hribar : Spoznajmo Javacript, Flamingo trade, 19982. Tomaž Kolšek : Krivulje in površine v CAD ( predavanje ), Ljubljana 1997
3. Watt Allan : Fundamentals of Three-Dimensional Computer Graphics, Addison-Wesley Publishing Company 1989
4. Farin Gerald : Curves and Surfaces for Computer Aided Geometric Design, Academic Press inc.-Harcourt Brace Jovanovich Publishers, 1990
Anton Hribar
e-mail:[email protected]