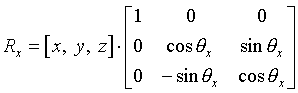
RPK - seminar |
Domen Otoničar |
V okviru vaj predmeta računalniško podprto konstruiranje sem dobil nalogo v obliki seminarja. Zahteva naloge je bila izdelati program, v katerem se nariše poljubno 2D ploščo, na kateri se izriše vzorec. To ploščo lahko nato poljubno premikamo v 2D in rotiramo v 3D prostoru. Pri tem moramo za spreminjanje lege plošče uporabljati deformacijske matrike, ki so opisane kasneje.
Program sem napisal s pomočjo programskega orodja Java Development Kit (JDK1.2).
Purpose of this research project is to show 2D plate with pattern translating in 2D space and rotating in 3D space. To modify the position and orientation of the plate, we must use deformation matrix.
Vhodne podatke (to so ogljišča poljubno velike plošče) vnašamo s klikom miške,
pri čemer se na tem mestu nariše točka. Vse točke plošče se shranijo v vektor (
tocke.addElement(new Point(e.getX(), e.getY()));), ki ga nadalje uporabljamo za izračun
translacij in rotacij. S pritiskom na gumb "OK" potrdimo končno število točk
v večkotniku in ukažemo izris večkotnika.
Za izdelavo mreze je potrebno določiti število polj vmreži. Nato se v odvisnosti od vrste lika (trikotnik, štirikotnik) razdeli stranice lika na toliko delov. Pri tem novo dobljene točke sharnimo v nove vektorje, ki jih pozneje uporabljamo pri izračunu translacije in rotacije. Mrežo narišemo tako, da takoj ko smo s pritiskom na gumb "OK" narsali ploščo, še enkrat pritisnemo na gumb "OK" in izrisala se bo mreža. Naloga je narejena tako, da je risanje mreže možno le za poljubni trikotnik ali štirikotnik, saj pri večkotnikih pride do problema določitve presečišča mreže s stranicami večkotnika.
Translacijo lika izvajamo s programsko funkcijo "mouseDrag", ki iz ekrana pobira trenutni položaj kurzorja, in ga vnaša v izračun za translacijo lika. Pri tem se vse točke lika in vse točke mreže enako pomaknejo za deltaX oz. deltaY, ki je enak dolžini vlečenja miške.
Rotacijo sem izračunal s pomočjo rotacijskih matrik za 3D prostor. Vrednosti rotacije (kota thetaX in thetaY) vanšamo tako kot pri translaciji s funkcijo "mouseDrag", pri čemer je vrednost vlečenja miške v x smeri vrednost rotacije okrog osi y v kotnih stopinjah (thetaY), vrednost vlečenja miške v y smeri pa vrednost rotacije okrog osi x v kotnih stopinjah (thetaX).
Matrika za rotacijo okrog x osi:
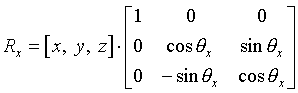
Matrika za rotacijo okrog y osi:
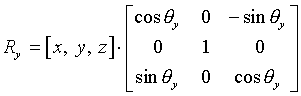
Matrika za rotacijo okrog z osi:
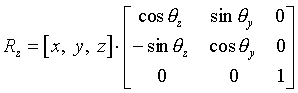
V mojem primeru nisem upošteval rotacije okrog osi z (toje tista os, ki gleda v ekran), ker je to rotacijo mogoče doseči s kombinacijo rotacije okrog osi x in y. Rotacijska matrika, ki sem jo uporabljal v programu je tako produkt matrik Rx in Ry.
R = Rx * Ry
Tako dobimo enačbo za izračun točk plošče po rotaciji:
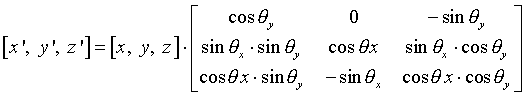
Dobljene točke ponevno vpišemo v vektor in jih narišemo na novem mestu in tako dobimo rotacijo lika.
Program je napisan v jeziku Java Development Kit 1.2.. Program sem pisal v obliki "applet"-a, kar pomeni, da program lahko deluje samostojno na različnih pregledovalnikih Html kode, če le podpirajo Javo. Program pa lahko pregledujemo tudi z "appletviewer"-jem. Kodo programa pišemo v keterem koli editorju in jo shranimo s končnico *.java. Ta program moramo najprej prevesti z ukazom "javac" (java compile), pri čemer dobimo program s končnico *.class. V editorju pa moramo napisati še Html kodo, ki bo klicala program s končnico *.class. Pri tem mora biti ime Html kode enako kot je ime programa s končnico *.class oz. *.java.
Ime programa: Lin.java
Ime HTML datoteke: Lin.html
Zagon programa: appletviewer Lin.html
Ce vas pregledovalnik podpira JDK1.2 lahko direktno zazenete program, sicer pa ga morate posneti na disk in zagnati z appletviewer-jem.
Naloga je pokazala možnosti programiranja grafike, ki je že nakaj časa v svetu računalnikov zelo v ospredju, predvsem v programih za risanje in pa v grafično vedno bolj zapletenih in zahtevnih računalniških igrah ter simulacijah. Za tako programiranje je potrebno imeti in obvladati ustrezen programski jezik. Za tako programiranje je najbolj primeren programski jezik, ki že vsebuje obsežne knjižnice podatkov za programiranje. V mojem primeru, ko sem programiral v programskem jeziku Java Development Kit 1.2 sem tako uporabljal Class-e, ki vsebujejo že narejene funkcije za določene naloge. Vendar da bi lahko uporabljal vse obstoječe knjižnice je potrebno kar nekaj izkušenj, da veš ali pa slutiš, kaj je že, ali pa bi lahko bilo že narejeno. Tako bi mi lahko v pomoč prišel 3D dodatek za JDK1.2.1., ki pa ga nisem imel. Tako sem moral funkcije za 3D rotacijo sam napisati. Ko sem pričel programirati z JDK1.2 sem k programu pritopil čisto na novo, saj do tedaj nisem še programiral z njim, ali pa z jezikom C, ki mu je precej podoben. Vendar pa odličen tutorial omogoča hitro učenje tega jezika, hitrost programiranja pa omogočajo že prej omenjene knjižnice. Celoten zapis programa pa je manj obsežen, kot bi bil zapis ekvivalentnega programa v jezijku C ali Fortran.
Foley & Van Dam: Principles of Computer Graphics
Wan Allan: 3D Computer Graphics
Eric Weisstein's Encyclopedia of Mathematics: http://treasure-troves.wri.com/math/