
3.0 Osnove standarda DIN 7991
3.1 Izris vijaka po standardu DIN 7991
3.2 Podatki za vijake DIN 7991
3.0 Teoretične osnove
4.1 Transformacije
4.2 Zapis transformacij v kartezijevih koordinatah
4.3 Zapis transformacij v homogenih koordinatah
5.0 Osnovna zgradba programa
5.1 Izris vijaka
6.0 Popravljanje oziroma dodelava programa
6.1 Dodajanje novih vijakov
6.2 Vnos novih vijakov v program
The main purpose of our program is that we recognize the main structure of JavaScript and emulation Phigs. In our program we use all main part of JavaScrip. First task of our program is to calculate points in coordinat system. When we have the main points we going to our second task that was to drawing lines and radius between this points.Then we must include in our program some basic geometrical transformations in 3D space.So our lines (crew) could be moved, rotated and scaled in x and y direction.We simplify calculation of new points with writinig data in fields.
Seminarska naloga zahteva napisati program za izris 3D modela vijaka po DIN 7991.Program naj omogoča transformacije v 3D prostoru ter izbor določenega vijaka glede na mere iz seznama in prikaz le - tega kot mrežni 3D model . Omogočena mora biti možnost postavitve vijaka na določeno mesto glede na globalni koordinatni sistem.Omogočeno mora biti premikanje v vseh treh smereh x, y in z , skaliranje in rotacije okoli osi x', y' in z'. Te funkcije morajo biti izvedene tako, da se jih lahko izvaja interaktivno z izbiro v menijih in vnosom potrebnih vrednosti.
Standard DIN 7991 je standard, ki nam določa dimenzije vijaka z okroglo glavo s šest oglatim utorom. Vijak ima metrični navoj velikosti od M3 do M20.

|
M d [mm] |
P [mm] |
b [mm] |
dk [mm] |
e [mm] |
r [mm] |
S [mm] |
t [mm] |
w [mm] |
l [mm] |
|
3 |
0.5 |
18 |
6.72 |
2.3 |
0.1 |
2 |
1.1 |
0.25 |
30 |
|
4 |
0.7 |
20 |
8.96 |
2.87 |
0.2 |
2.5 |
1.5 |
0.45 |
30 do 40 |
|
5 |
0.8 |
22 |
11.2 |
3.44 |
0.2 |
3 |
1.9 |
0.66 |
35 do 50 |
|
6 |
1.0 |
24 |
13.44 |
4.58 |
0.25 |
4 |
2.2 |
0.7 |
40 do 60 |
|
8 |
1.25 |
28 |
17.92 |
5.72 |
0.4 |
5 |
3 |
1.16 |
50 do 80 |
|
10 |
1.5 |
32 |
22.4 |
6.86 |
0.4 |
6 |
3.6 |
1.62 |
55 do 100 |
|
12 |
1.75 |
36 |
26.58 |
9.15 |
0.6 |
8 |
4.3 |
1.8 |
65 do 100 |
|
(14) |
2.0 |
40 |
30.8 |
11.43 |
0.6 |
10 |
4.5 |
1.62 |
70 do 100 |
|
16 |
2.0 |
44 |
33.6 |
11.43 |
0.6 |
10 |
4.8 |
2.2 |
80 do 100 |
|
20 |
2.5 |
53 |
40.32 |
13.72 |
0.8 |
12 |
5.6 |
2.2 |
100 |
Translacija točke v 3D prostoru:






-Translacija
Ni možno prikazati translacije v kartezijevih koordinatah.
-Rotacija okrog z osi:

-Rotacija okrog y osi:

-Rotacija okrog x osi:

-Skaliranje:

-Translacija:

-Rotacija okrog z osi:

-Rotacija okrog y osi:

-Rotacija okrog x osi:

-Skaliranje:

Program je zgrajen tako, da sem na začetku definiral obliko uporabniške strani in definiral velikost prikazovalnega zaslona.Funkcija Rotacija ima osem spremenljivk, ki jih lahko spreminjamo tako, da spremenimo vrednosti v okvirčkih na zaslonu in potem pritisnemo na gumb "Izris mrežnega modela
" ali na gumb "Izris robov vijaka".Najprej sem definiral točke krogov, tako da sem krožnico opisal s 64 točkami za katere sem podatke jemal iz baze podatkov.Vse točke vijaka so postavljene glede na lokalni koordinatni sistem, ki ima središče na sredinski črti med steblom in glave vijaka.Vse te točke sem potem transformiral s pomočjo
transformacijske matrike.Definiral sem še točke glavnega koordinatnega sistema.Vse te točke sem potem še rotiral okrog osi y in z in premaknil v vseh treh smereh in sem postavil zaslon v ravnino y-z.Potem sem definiral še povezovalne črte med krogi, katerih točke se nahajajo na sečišču krožnice in pravokotnice na transformirano os x' skozi transformirano središče krožnice.Vse te črte sem izrisal s PHIGS ukazi.Če pade slika izven zaslona se avtomatično celotna slika toliko pomanjša, da pade celotna slika na zaslon.Najprej sem naredil program, ki izriše vijak tako, da se vidijo le skrajne robne črte vijaka, kar je s programerskega vidika težje naredit, ker pa se običajno riše mrežne modele vijaka, da je potem možna tudi osvetlitev posameznih ploskev vijaka sem izpopolnil program tako ,dam lahko izriše oba modela vijaka.Možno je tudi nastavljanje gostote mreže vijaka.-Vijak v izhodiščnem položaju.Globalni in lokalni koordinatni sistem se pokrivata.

-Translacija vijaka v smereh X, Y in Z.

-Rotacija vijaka okrog Z' osi.

Popravljanje programa oziroma dodajanje novih vijakov je zelo enostavno. Pod direktorijem pod katerim imamo shranjen program poiščemo datoteko, ki se imenuje baza.js, to datoteko odpremo s pomočjo programa WordPad. V odprto datoteko vpišemo nove podatke za želeni vijak, nato pa v program dodamo ta vijak.
Izgled baze podatkov (baza.js):
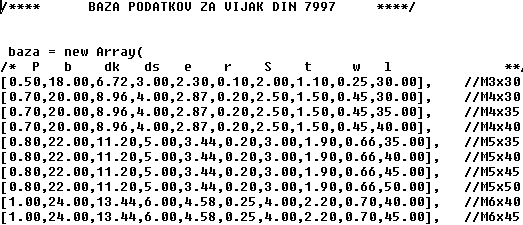
V zgoraj navedeno bazo podatkov baza.js dodajamo nove vijake z vpisom naslednje vrstice v datoteko baza.js:
![]()
Za vnos novih vijakov v program moramo v zavesni meni vnesti nov vijak to storimo tako da v program 3dtran.html v 13 vrstico od zgoraj pred
</SELECT
napišemo
<OPTION M(d - premer) x (L - dolžina stebla).
Po opravljenem postopku je potrebno ponovno naložiti brskalnik Netscape Navigator ali Internet Explorer (osvežitev ni dovolj).
Pri izdelavi seminarske naloge sem spoznal osnove jezika Java Script in emulacijo grafične knjižnice PHIGS, ki na omogoča izris črt. V programu sem se seznanil z izračunom točk za izris vijaka, nato z sami izrisom črt. Najpomembnejši del progama pa so osnovne geometrijske transformacije v 3D geometrijskem prostoru. S pomočjo transformacij dosežemo da lahko vijak premikamo po zaslonu ga povečujemo in rotiramo. Vse izračunane podatke smo zapisovali v polja in s tem smo si zelo poenostavili izračun novih točk pri geometrijskih transformacijah.
1. DIN standardi, DIN 7991
2. Peter Hribar, Spoznajmo Javascript, izdaja: Flamingo trade, 1998
3. Peter Hribar, HTML 4.0, izdaja: Flamingo trade, 1998
Avtor: MATEJ PETRIČ
Mentor: JANEZ VRHOVEC
Zadnja sprememba: 20.8.1999