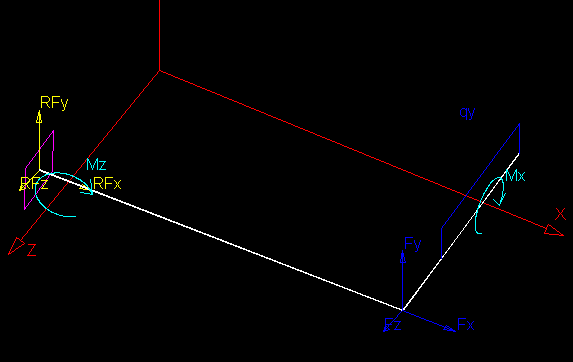
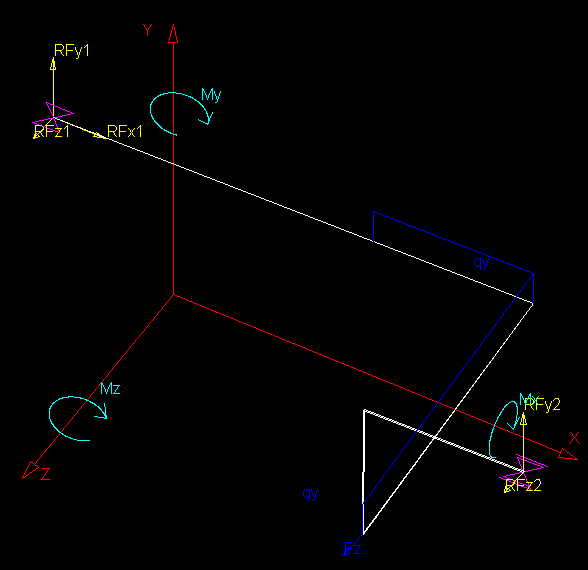
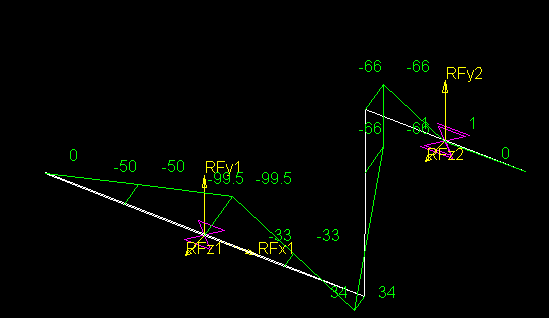
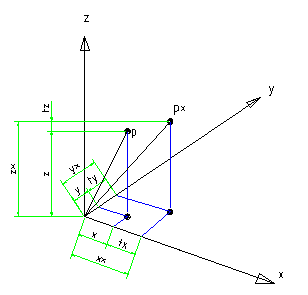
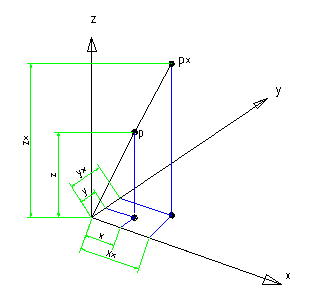
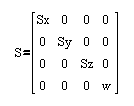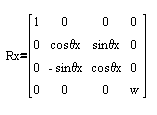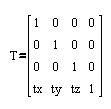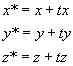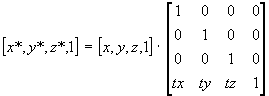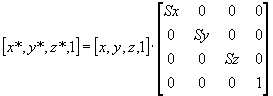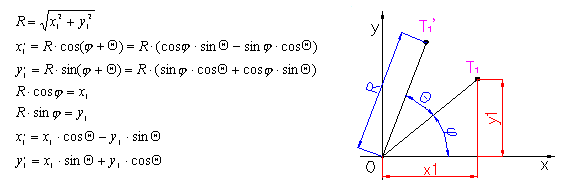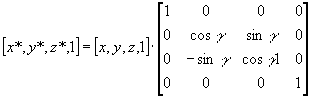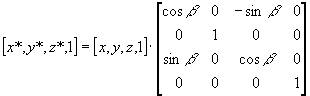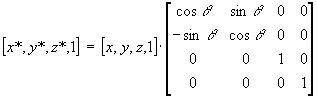Uporaba enacbe kroznice za izris krogov in funkcijo za izris sile
function izrisKroga(sx,sy,pkotx,pkotz,pkoty,texst,color,r){
var xkrog=new Array();
var ykrog=new Array();
var deg=Math.PI/180;
var tockaKrog=new Array();
var tockaPuscicaKroga=new Array();
for(var k=0; k 281; k++){
zkroga=r*Math.cos(k*deg);
ykroga=r*Math.sin(k*deg);
xkroga=0;
rotx=xkroga;
roty=ykroga;
rotz=zkroga;
rotacijaPoljubno(rotx,roty,rotz,pkotx,pkotz,pkoty);
tockaKrog[k]=new Ppoint(x111+sx,y111+sy);
}
var tockaS=new Ppoint_list(k, tockaKrog);
pset_line_colr_ind(color);
pset_text_colr_ind(color);
ptext(new Ppoint(tockaKrog[280].x+0.03, tockaKrog[280].y+0.03), texst);
ppolyline(tockaS);
function izrisSile(sx,sy,skotx,skoty,skotz,texst,color){
var sila=new Array();
sila[0]=new Array(0,0,0);
sila[1]=new Array(0.1,0,0);
sila[2]=new Array(0.08,0,0.005);
sila[3]=new Array(0.08,0,-0.005);
sila[4]=new Array(0.1,0,0);
var tockaSila=new Array();
for(var k=0; k 5; k++){
rotx=sila[k][0];
roty=sila[k][1];
rotz=sila[k][2];
pkotx=skotx;
pkoty=skoty;
pkotz=skotz;
rotacijaPoljubno(rotx,roty,rotz,pkotx,pkotz,pkoty);
tockaSila[k]=new Ppoint(x111+sx,y111+sy);
}
var tockaS=new Ppoint_list(k, tockaSila);
pset_line_colr_ind(color);
pset_text_colr_ind(color);
ptext(new Ppoint(tockaSila[4].x+0.002, tockaSila[4].y+0.002), texst);
ppolyline(tockaS);
}