
Englih Abstract
Computer program constructed in JavaScript language calculates internal tensions in a rope, for different types of vertical loading.
Internal tensions are also shown graphically. The dimensions and load conditions are optional.
Definicija naloge
Izdelajte program, ki bo omogocal vnos geometrije (razmak podpor), postavitve in velikost sil, ter vnos dodatnega podatka (celotno dolzino vrvi, horizontalno silo ali poves pod eno izmed sil).Program mora izracunati notranje sile v vrveh in njihove vrednosti izrisati na ekran. Program izdelajte s programskim jezikom Java ali JavaScript (izris s pomocjo PHIGS knjiznice).
Teoreticne osnove
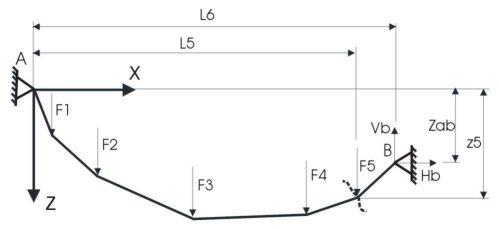
Vrv je enodimenzionalni konstrukcijski element. Idealna vrv je homogena, toga v smeri svoje osi in le v tej smeri prenasa natezno osno silo, v vseh ostalih smereh in nacinih obremenitev pa ima lastnosti popolne gibkosti. Ne prenasa tlacne osne sile, upogibnega momenta, precnih sil in torzijskega momenta. Kot realni priblizek vrvi lahko uporabljamo verige, pletenice, kot tudi niti in vlakna. V nasem primeru bomo obravnavali samo vrv obremenjeno z vertikalnimi tockovnimi silami. Vse sile naj delujejo v isti ravnini in njihova velikost je toliksna, da lahko zanemarimo linijske obremenitve vrvi zaradi lastne teze ali katerekoli druge zvezne obremenitve. Vrv je obicajno na obeh straneh clenkasto vpeta v podporno tocko ali obesisce (A in B). Med znane podatke sodijo velikosti vertikalnih obremenitev (F1, F2, F3....), razlika višin med podporama (Zab) in dolzine med posameznimi silami (L1, L2, L3....), ter celotna razpetina (L6) (slika 1).

Ker sta podporni tocki fiksni, je sistem enkrat staticno nedolocen in potrebujemo za dolocitev reakcij se en podatek, ki ga dobimo iz dodatnega pogoja. Pri tem obstaja vec moznosti:
| Podamo dolzino celotne vrvi (L). Taksen primer program resuje po iterativnem postopku. | |
| Podamo horizontalno komponento osne sile (H) v vrvi. To v praksi obicajno dosezemo tako, da je eno izmed obesisc | |
| izvedeno s primerno konstrukcijo, ki nam omogoca zanano konstantno vrednost sile H | |
| Podamo ordinato enega izmed prijemalisc vertikalnih obremenitev na vrvi. |
Pri racunanju reakcij se bomo v nasem primeru postavili v obesisce A in ob upostevanju koordinatnega sistema postavili tri ravnotezne enacbe (enacbe 1, 2 in 3).
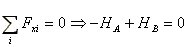 |
(1) |
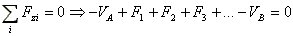 |
(2) |
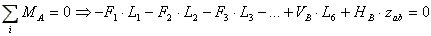 |
(3) |
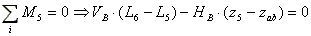 |
(4) |
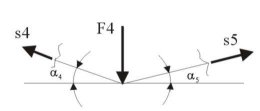
Ko imamo poznane vse zunanje sile, notranje dolocamo po poljih. Izrezemo primejalisca iz vrvi in postavljamo po dva ravnotezna pogoja za ravninski sistem s skupnim prijemaliscem (slika 3 in enacbi 5 in 6). Zacnemo pri enem od obesisc, kjer poznamo velikost sile v vrvi in nato zaporedno izracunamo napetosti za preostala polja.
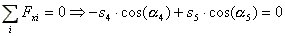 |
(5) |
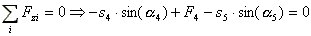 |
(6) |
Navodila za uporabo programa in zagon programa
Navodila za uporabo programa so zapisana v pomoci.
Pomoc
User information and start of a program
User information are written in help.
Help
Katalog
V katalogu so zbrane dimenzijske vrednosti in pretrzne vrednosti za jeklene vrvi in verige. Podatki so povzeti po Krautovem strojniškem prirocniku.
Katalog
Zakljucek
Najvecje tezave za izracun sil v vrvi so bile pri pogoju a, ko imamo poznano dolzino vrvi. Program v tem primeru racuna iterativno in je potrebno predvideti številne mozne kombinacije vstavljenih podatkov. Tako se lahko zgodi, da ob "neugodnih" podatkih potrebuje program vec casa ali pa se zgodi, da resitev preskoci. Da se to nebi zgodilo bi bilo potrebno dolociti manjše korake pri racunanju, kar pa bi lahko zelo podaljsalo cas racunanja. Z velikostjo teh korakov pa je pogojena tudi natancnost rezultatov.
V primeru B, ko imamo poznano horizontalno silo, dobimo takoj tocne rezultate.
Ko pa poznamo pozicijo prijemalisca ene sile je racunanje prav tako hitro, vendar se lahko zgodi, da vstavimo podatke, ki niso v skladu z naravo vrvi, ki je po predpostavkah povsem gibka in prenasa samo natezne napetosti. Ker je skoraj nemogoce predvideti vse kombinacije, v katerih bi se v taksnem primeru na ekran izpisalo opozorilo, sem pri izrisu vrvi podal se izris pozicije sil in njihovo smer. Tako lahko iz izrisanega poteka vrvi in sil, sklepamo o napaki pri vnosu vertikalne pozicije sile.
V prihodnosti bi to seminarko nalogo lahko se nadgradili z racunanjem poljubnega stevila vertikalnih sil v vrvi, pri poljubni vertikalni linijski obremenitvi, z upostevanjem lastne teze in s samodejnim izborom jeklene vrvenice ali verige iz kataloga.
Literatura
Osnove tehniske mehanike 1- STATIKA, Milan Mursic, Slovensko drustvo za mehaniko, Ljubljana 1993
Java programiranje za internet, Uros Mesojedec, Pasdadena, Ljubljana 1997
Krautov strojniski prirocnik, Bojan Kraut, Tehniska zalozba Slovenije, Ljubljana 1993