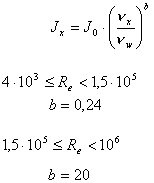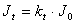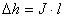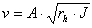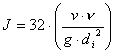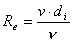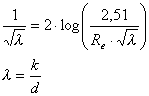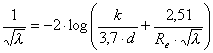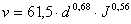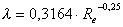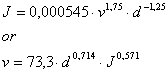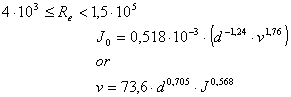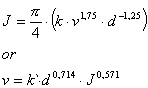Seminarska naloga

VIŠINSKE IZGUBE V TERMOPLASTIČNIH CEVEH ZA PRETOK TEKOČIN POD TLAKOM

Head loss in termoplastic pipes under preasure

KAZALO

1.Povzetek

2.Uvod

3.Matematične osnove

4.Razčlenitev problema na faze

5.Opis rešitve problema

6.Program

7.Zaključek

1.Summary

- presentation of used symbols

Name of symbol	Mark	Unit
Average velocity	v	m/s
Average internal diameter	d	m
Head loss	h	m
Head drop	J	m/m
Reynolds number	Re	/
Kinematic viscosity	V	m²/s
Pipe length	l	m
Temperature of liquid	t	^oC
Temperature correction factor	k_t	/

- summary of how program is done

Program is based on standard, so if you want to use the program you have to give some data, and that is fluid velocity, average internal diameter of pipe, kinematic viscosity if the fluid is not water, pipe length and temperature of liquid. Then the program assess the Reynolds number which is used for selection of which formula to use for calculate the head drop in pipe. When the Reynolds is calculated program choose between two formulas and it picks one and calculate the head drop. After that, program make temperature correction and correction if the choosen fluid have diffrent kinematic viscosity than water. Temperature correction is based on table which is present in mathematical bases. At the and program calculate head loss with formula which is also present in mathematical bases.

1.Povzetek

- predstavitev uporabljenih simbolov

Naziv veličine	Oznaka	Enota
Povprečna hitrost	v	m/s
Notranji premer cevi	d	m
Izgube	h	m
Izgube na meter	J	m/m
Reynoldsovo število	Re	/
Kinematična viskoznost	V	m²/s
Dolžina cevi	l	m
Temperatura tekočine	t	^oC
Temperaturni korekcijski faktor	k_t	/

- povzetek delovanja programa

Program je po standardu narejen tako, da uporabnik vnese hitrost tekočine, notranji premer cevi, kinematično viskoznost snovi v kolikor to ni voda, dolžino cevi ter temperaturo te tekočine. Nato program izračuna Reynoldsovo število, ki služi za izbiro formule za izračun izgub na meter. Ko je Reynolds določen se izračuna izgube na meter za vodo ter se nato koregira na izbrano tekočino. Na koncu pa se izvede še interpolacija temperaturnega faktorja in končni izračun izgub na meter ter končni rezultat, ki pa so izgube v cevi.

2.Uvod

Program izračunava vrednost višinskih izgub, ki se pojavijo v plastičnih ceveh pod tlakom in sicer računa izgube v metrih. Izgube so odvisne od notranjega premera cevi, vrste tekočine oziroma njene kinematične viskoznosti, hitrosti tekočine v cevi ter od temperature te tekočine. Tako program izračuna izgube, ko dobi te vhodne podatke. Same enačbe za izračun izgub so dokaj preproste, vendar pa jih je več, katero pa uporabimo pa zavisi od Reynoldsovega števila, ki ga program izračuna ter nato preko IF stavka izbere ustrezajočo formulo. Največji problem pa je interpolacija temperaturno korekcijskega faktorja, ki pa je ravno tako narejena preko IF stavkov. Ostali izračuni pa so enostavni, tako da ostane samo še izpis rezultatov, ki se izpišejo v za to določena mesta na ekranu.

Nazaj na kazalo

3.Matematične osnove

- izračun J₀ - za vodo pri 20 ^oC:

- izračun J_x - za x-o tekočino drugačno od vode:

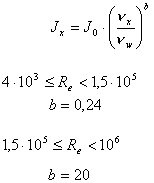
- temperaturni korekcijski faktor:

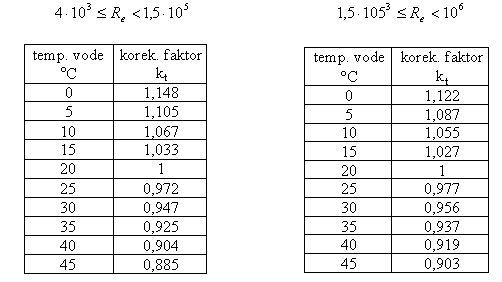
- temperaturna korekcija:

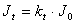
- izračun višinskih izgub:

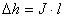
Predstavitev formul iz dodatka A:

- Chezy formula:

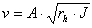
r_h-hidravlični radij
A-koeficient

- Hagen and Poiseuille formula:

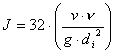
d_i-notranji premer cevi
v-dinamična viskoznost
g-gravitacijski pospešek

- Reynolds number:

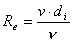
- Von Karman formula:

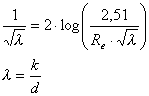
- Colebrook formula:

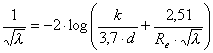
0,001-k-0,007 za plastične cevi

- Hazen-Williams formula:

C-Hazen-Williamsov koeficient

- Strickler formula:

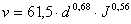
- Blasius formula:

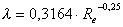
- Tison formula:

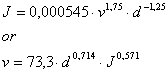
- Samo za plastične cevi razvita formula:

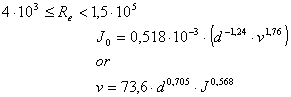
- SNV formula:

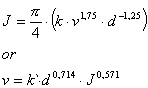
Nazaj na kazalo

4. Razčlenitev problema na faze

Proglam je razčlenjen na 6 delovnih faz, in sicer naslednjih:

Faze	Opis
1	Izračun Reynoldsovega števila
2	Izračun izgub za vodo pri 20 ^oC
3	Interpolacija oziroma določitev temperaturno korekcijskega faktorja
4	Izračun temperaturno koregiranih izgub
5	Izračun izgub za podano tekočino
6	Končni izračun izgub glede na dolžino cevi

V programu je vsaka faza izdelana posebej kot funkcija, nato pa so vse funkcije skupaj združene v celoto.

5. Opis rešitve problema

- faza 1 (Izračun Reynoldsovega števila )

Reynoldsovo število se enostavno izračuna po zgoraj prikazani formuli. Podatke za izračun pa mora podati uporabnik. In to je hitrost medija, notranji premer plastične cevi ter kinematično viskoznost medija, ki se pretaka po cevi.

- faza 2 (Izračun izgub za vodo pri 20 ^oC )

Standardni preračun je narejen tako, da se računa izgube za vodo pri 20 ^oC, nato pa se te izgube s faktorji in razmerji koregira za podano temperaturo in medij. Tako se mora najprej določiti izgube kot, da se voda pretaka po cevi. Ta izračun zavisi od vrednosti Reynoldsovega števila, tako da sta na voljo dve formuli , katero pa uporabimo, pa je omejeno z vrednostjo Re. Tako mora program izbrati pravo in izračunati izgube. To je storjeno z naslednjim delom programa:

function izgube(d,v,Re)
	{
	if (Re>=4000 && Re<150000)
		{
		var J=5.37*0.0001*(Math.pow(d/1000,-1.24)*Math.pow(v,1.76));
		return J;
		}
	else if (Re>=150000 && Re<1000000)
		{
		var J=5.79*0.0001*(Math.pow(d/1000,-1.20)*Math.pow(v,1.80));
		return J;
		}
	else	{
		var J="Podatki ne ustrezajo standatdnemu izračunu!";
		return J;
		}
	}

- faza 3 (Interpolacija temperaturno korekcijskega faktorja )

Temperaturno korekcijski faktor je v standardu zapisan v dveh tabelah, ki zavisita od Reynoldsovega števila. V tabelah je v odvisnosti od temperature zapisan korekcijski faktor. Temperatura v tabeli se povečuje za pet stopinj celzija tako, da je potrebno za vmesne temperature ta faktor interpolirati. To je v programu narejeno s pomočjo IF stavka, ki v prvi fazi izbira glede na Reynoldsovo število, v drugi fazi pa glede na podano temperaturo. Del tega programa je spodaj tudi izpisan:

	
function interpolacija(x,Re)
	{
	var y;
	if (Re>=4000 && Re<150000)
		{
		if (x>=0 && x<5)
			{
			y=1.148+((1.105-1.148)/(5-0))*(x-0);
			return y;
			}
		else if (x>=5 && x<10)
			{
			y=1.105+((1.067-1.105)/(10-5))*(x-5);
			return y;
			}
		else if (x>=10 && x<15)
			{
			y=1.067+((1.033-1.067)/(15-10))*(x-10);
			return y;
			}
		else if (x>=15 && x<20)
			{
			y=1.033+((1-1.033)/(20-15))*(x-15);
			return y;
			}
		else if (x>=20 && x<25)
			{
			y=1+((0.972-1)/(25-20))*(x-20);
			return y;
			}
		else if (x>=25 && x<30)
			{
			y=0.972+((0.947-0.972)/(30-25))*(x-25);
			return y;
			}
		else if (x>=30 && x<35)
			{
			y=0.947+((0.925-0.947)/(35-30))*(x-30);
			return y;
			}
		else if (x>=35 && x<40)
			{
			y=0.925+((0.904-0.925)/(40-35))*(x-35);
			return y;
			}
		else if (x>=40 && x<=45)
			{
			y=0.904+((0.885-0.904)/(45-40))*(x-40);
			return y;
			}
		else 	{
			y="Podatki ne ustrezajo standardnemu izračunu!"
			return y;
			}

- faza 4 (Izračun temperaturno koregiranih izgub )

Po izračunu temperaturno korekcijskega faktorja se predhodno izračunane izgube koregirajo po enačbi navedeni v matematičnih osnovah. To je preprost izračun ko korekcijski faktor le pomnožimo z izgubami za vodo pri 20 ^oC.

- faza 5 (Izračun izgub za podano tekočino)

Ker imajo tekočine različne kinematične viskoznosti, so tudi izgube različne. Zato je potrebno izgube, ki so Izračunane za vodo koregirati za razmerje med viskoznostima med vodo ter podane tekočine. Kot je videti iz enačbe, ki je podana v matematičnih osnovah je ta izračun odvisen tudi od velikosti Reynoldsovega števila od katerega zavisi faktor b. Zato program zopet preko IF stavka določi faktor b ter nadalje izračuna vrednost izgub za podani medij oziroma tekočino. To je podano v spodnjem delu programa.

function izgube1 (V1,J,Re)
	{
	if (Re>=4000 && Re<150000)
		{
		var Jx=J*Math.pow((1.01/V1),0.24);
		return Jx;
		}
	else if (Re>=150000 && Re<=1000000)
		{
		var Jx=J*Math.pow((1.01/V1),20);
		return Jx;
		}
	else	{
		var Jx="Podatki ne ustrezajo standardnemu izračunu!";
		return Jx;
		}
	}

- faza 6 (Končni izračun izgub glede na dolžino cevi )

Ko program izračuna dejanske izgube za podano tekočino, moramo te izgube samo še pomnožiti z dolžino cevi, ker so predhodno izračunane izgube izražene na en meter cevi. Tako dobimo končni rezultat, kar so izgube v cevi izražene v metrih.

6. Program

VHOD V PROGRAM - START THE PROGRAM

7. Zaključek

Standardni preračun višinskih izgub je dokaj enostaven saj moramo uporabiti le štiri formule za končni rezultat. Zato je temu primerno enostavno napisan tudi program, ki je lahko razumljiv za vse uporabnike. Zaradi enostavnosti pa je malo bolj obsežen, vendar za samo funkcijonalnost to ni tako pomembno.

Nazaj na kazalo

Seminarska naloga

VIŠINSKE IZGUBE V TERMOPLASTIČNIH CEVEH ZA PRETOK TEKOČIN POD TLAKOM

Head loss in termoplastic pipes under preasure

KAZALO

1.Summary

- presentation of used symbols

- summary of how program is done

1.Povzetek

- predstavitev uporabljenih simbolov

- povzetek delovanja programa

2.Uvod

3.Matematične osnove

Predstavitev formul iz dodatka A:

4. Razčlenitev problema na faze

5. Opis rešitve problema

- faza 1 (Izračun Reynoldsovega števila )

- faza 2 (Izračun izgub za vodo pri 20 oC )

- faza 3 (Interpolacija temperaturno korekcijskega faktorja )

- faza 4 (Izračun temperaturno koregiranih izgub )

- faza 5 (Izračun izgub za podano tekočino)

- faza 6 (Končni izračun izgub glede na dolžino cevi )

6. Program

7. Zaključek

- faza 2 (Izračun izgub za vodo pri 20 ^oC )