13.6 Mehanizmi s poljubnimi zglobi
Kazalo vsebine:
Mehanizmi s poljubnimi zglobi
Razložite prostostne stopnje različnih zglobov
in nato za mehanizem z 9 prostostnimi stopnjami izdelajte program, ki bo izrisal
potovalno krivuljo pomembnih točk in hitrost na koncu palice. Glej VDI 2156.
Prostostne stopnje so opisane v smernici VDI 2156 in so rezultat dela odbora za
prostorska gonila.
Za prostorsko ročično gibanje potrebujemo najmanj dva predmeta, ki ju
obravnavamo enega glede na drugega. Glavni deli mehanizma za ročino gibanje
so podstavek, členki, palice, ročice, drsniki,... Dva predmeta, ki sta
prosto ležeča v prostoru imata 6 prostostnih stopenj (tri translacije
in tri rotacije). Če jima zmajšamo število prostostnih stopenj imata
predmeta še 1-5 prostostnih stopenj.
Za vsako vrsto prostostne stopnje so uvedli oznako. Oznaka je črka (D,S ali W) in
vsaka ima svoj pomen. Ker standard VDI izhaja iz nemščine pomenijo oznake naslednje:
- D-rotacija (Drehung-nemško)
- S-translacija (Schiebung-nemško)
- W-vijačenje (Windung,Scraubung-nemško)
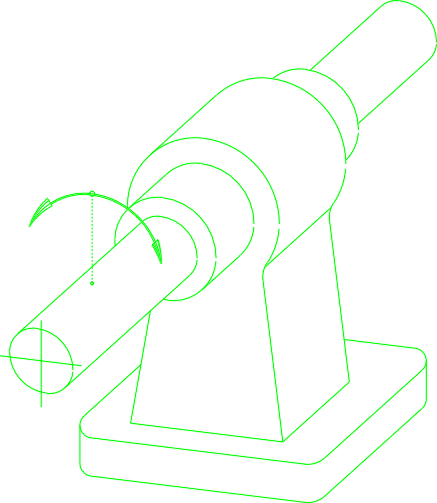
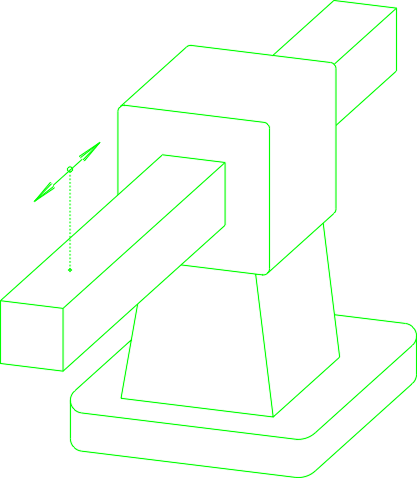
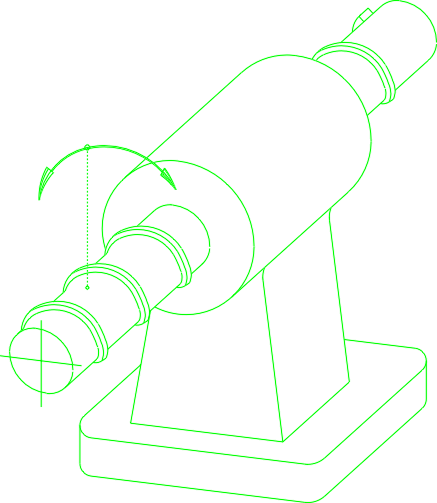
V zgoraj navedenih primerih smo imeli primere označevanja samo ene prostostne stopnje.
Z nadgradnjo osnovnih oznak, lahko označujemo tudi več prostostnih stopenj. S
kombinacijo črk in številk dobimo npr:
- D3-mehanizem z tremi rotacijami okoli treh osi
- DS-mehanizem z rotacijo in translacijo
- DS2-mehanizem z rotacijo in dvema translacijama
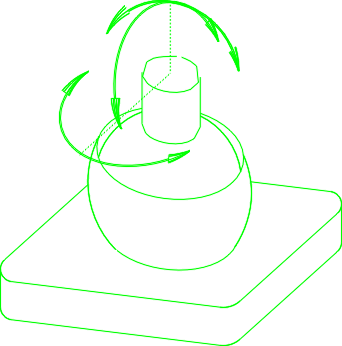

 D-D3=DS=D3
D-D3=DS=D3
V standardu VDI 2156 je podan primer mehanizma z 9. prostostnimi stopnjami, kateremu je potrebno
določiti potovalno krivuljo in hitrosti pomembnih točk.
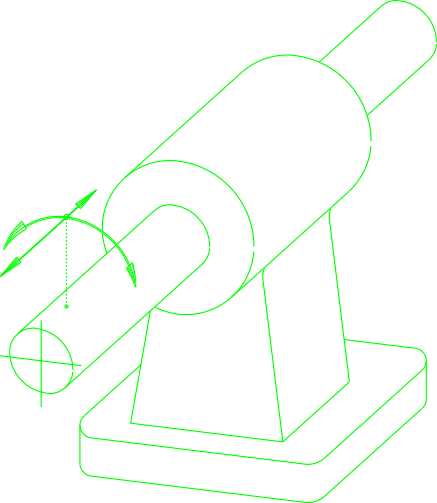
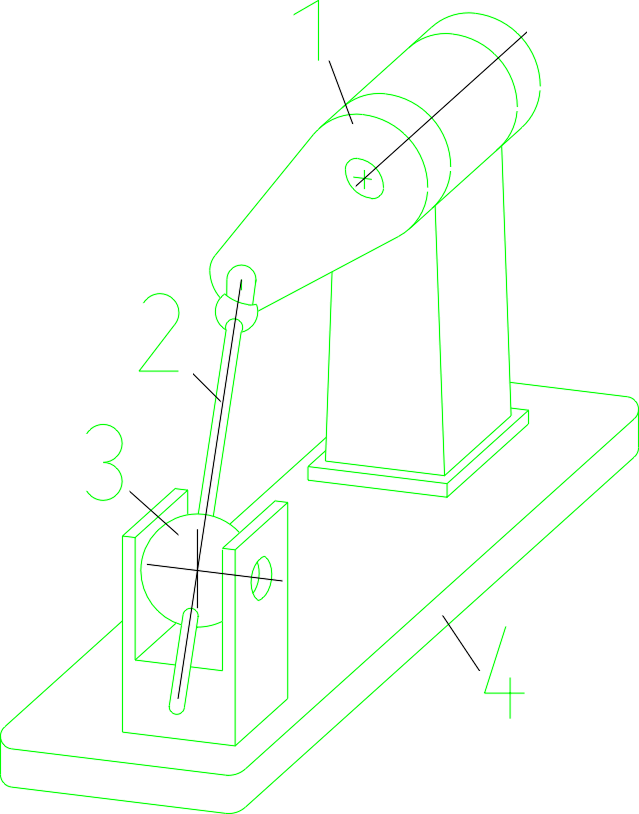
Mehanizem je sestavljen iz več delov. Iz slike zgoraj lahko vidimo, da ročica 1 rotira okoli
osi z, zato ima oznako D . Palica 2 je pritrjena na ročico 1 z členkom, ki ima tri prostostne
stopnje (rotacije okoli x, y in z osi) zato ima oznako D3. Palica 2 ima dve prostostni stopnji
rotacijo in translacijo, zato oznaka DS. Krogla 3 ima tri prostostne stopnje (rotacije okoli x, y in z osi)
in ima oznako D3. Če sestavimo vse skupaj imamo devet prostostnih stopenj, insicer
D-D3=DS=D3 (1+3+2+3=9).
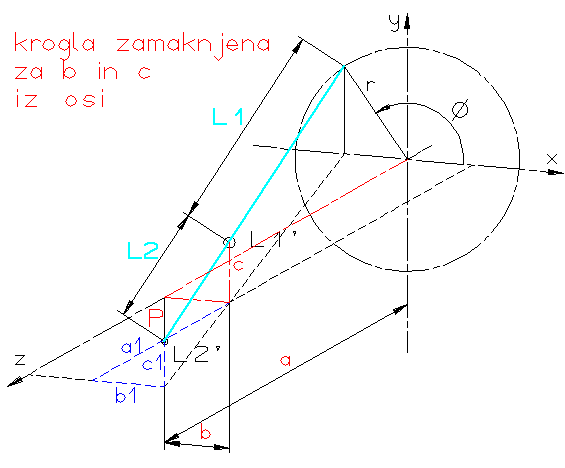
Za razumevanje delovanja programa potrebujemo enačbo po kateri se
točke Pi transformirajo v nove točke PiT. Če opazujemo sliko spodaj
lahko vidimo, da lahko predmete postavimo v različne položaje. Pomembna je pozicija krogle 3,
glede na ročico 1, ki je lahko premaknjena iz soosnosti (iz osi z). Iz skice je vidno, da je
soosnost dosežena če sta razdalji b=0 in c=0. V program vnesemo naslednje veličine: L,
a, b, c, in kotno hitrost ročice 1 omego!

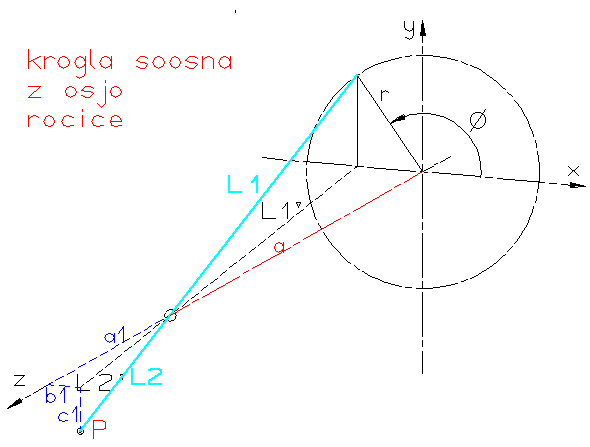
Če postavimo kroglo 3 v isto os kot je ročica 1 dobimo enostavno gibanje krivulje točke P,
katero opazujemo (krog).
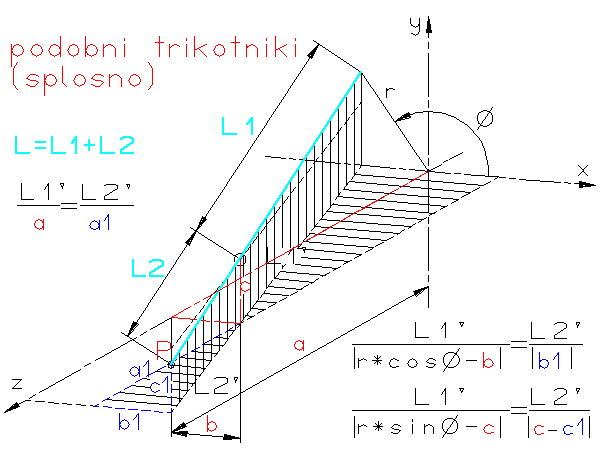
Izračun koordinat točke P glede na podane vhodne podatke (L, a, b, c, ...). Za izračun
so pomembni podobni trikotniki na sliki.
Programiranje v Javascript-u je enostavno, če uporabljas veliko dodatnih ordij, ki javljajo napake in ti omogočajo tudi pomoč.
Sam tega nisem imel, zato mi je v začetku programiranje v Javascript-u povzročalo precej težav. Zelo zamudna in neznana
je grafika, saj sem moral preučiti veliko primerov preden sem razumel, kako poteka programiranje grafike s pomocjo grafične
knjižnice PHIGS.
Pri programiranju so mi bili v veliko pomoč objavljeni primeri na LECAD-ovi domači strani (primer; Riši Kocko). Del te kode
je prekopiran v mojo kodo. Ta del kode razumem in bi ga lahko tudi sam ustvaril.
- Peter Hribar : Spoznajmo JavaScript
- Bojan Kraut : Strojniški priročnik
- Jože Petrišič : Numerične metode in programiranje (predavanja)
- Tomaž Kolšek: Primeri programov JS (internet)
 D-D3=DS=D3
D-D3=DS=D3







