UNIVERZA V LJUBLJANI

FAKULTETA ZA STROJNIŠTVO

LABORATORIJ ZA RAČUNALNIŠKO PODPRTO KONSTRUIRANJE

SEMINARSKA NALOGA PRI PREDMETU

RAČUNALNIŠKO PODPRTO KONSTRUIRANJE

Univerzitetni študij

Predavatelj: prof. dr.Jože DUHOVNIK, dipl.inž.

Asistent: mag. Leon KOS, dipl.inž.

Izdelal: Martin DEŽELAK

avgust, 2000

4.23 Bresenhamov algoritem za črte in kroge z antialiasingom

Celoštevilčni algoritem za risanje črt in krogov omogoča hitro risanje na rasterske enote. Izdelati je potrebno program, ki v rastersko datoteko zapiše kroge in črte s tem, da izvede še antialiasing glede na barvo podlage.

Abstract

An accurate and efficent raster line-generating algorithm, developed by Bresenham, scan converts lines using only incremental integer calculations that can be adapted to display circles and other curves. Bresenham's algorithm is generalized to lines with arbitrary slope by considering the symmetry between the various octants and quadrants of the xy plane. More efficent circle algorithm are based on incremental calculation of decision parameters, as Bresenham line algorithm, which involves only simple integer operations. Bresenham's line algorithm for raster display is adapted to circle generation by setting up decision parameters for finding the closest pixel to the circumference at each sampling test. The circle equation, is nonlinear, so that square-root evaluations would be required to compute pixel distances from a circular path. Bresenham's circle algorithm avoids these square-root calculations by comparing the squares of the pixel separation distances.
Displayed primitives generated by the raster algorithms have a jagged, or stairstep, appearance because the sampling process digitizes coordinate points on an object to discrete integer pixel positions. This distortion of information due to low-frequency sampling is called aliasing. We can improve the appearance of displayed raster lines by applying antialiasing methods that compensate for the undersampling process.

KAZALO

Bresenhamov algoritem za risanje črt
Bresenhamov algoritem za risanje krogov
PPM format
Antialiasing
Primeri izrisa ppm datoteke glede na različne barve črt in podlage
Literatura

Bresenhamov algoritem za risanje črt

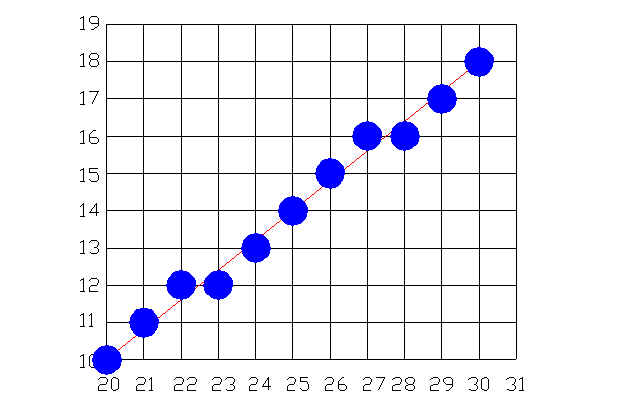
1. Korak
Zapišemo točki:
A(x1,y1) in B(x2,y2)

2. Korak
Izračunamo potrebne konstante:
deltax = x2 - x1
deltay = y2 - y1

3. Korak
Pregledamo pogoj:

- če je izpolnjen pogoj deltax >= deltay potem sledi:

d = (2 * deltay) - deltax
dinc1 = deltay * 2
dinc2 = (deltay - deltax) * 2
xinc1 = 1
xinc2 = 1
yinc1 = 0
yinc2 = 1

- drugače se izpolne pogoj:

d = (2 * deltax) - deltay
dinc1 = deltax * 2
dinc2 = (deltax - deltay) * 2
xinc1 = 0
xinc2 = 1
yinc1 = 1
yinc2 = 1

4. Korak
Pregled pogoja:

- če je:
x1 > x2 potem sledi
xinc1 = - xinc1
xinc2 = - xinc2

- če je:
y1 > y2 potem sledi:
yinc1 = - yinc1
yinc2 = - yinc2

5. Korak
x=x2
y=y2

6. Korak
- če je:

d < 0 potem sledi:
d = d + inc1
x = x + xinc1
y = y + yinc1

- drugače sledi:
d = d + inc2
x = x + xinc2
y = y + yinc2

7. Korak
STOP

Spremenljivke:
dinc1 = vrednost, ki jo dodamo d-ju, ko je d < 0
dinc2 = vrednost, ki jo dodamo d-ju, ko je d >= 0
xinc1 = vrednost, ki jo dodamo x-u, ko je d < 0
xinc2 = vrednost, ki jo dodamo x-u, ko je d >= 0
yinc1 = vrednost, ki jo dodamo y-u, ko je d < 0
yinc2 = vrednost, ki jo dodamo y-u, ko je d >= 0

Bresenhamov algoritem za risanje krogov

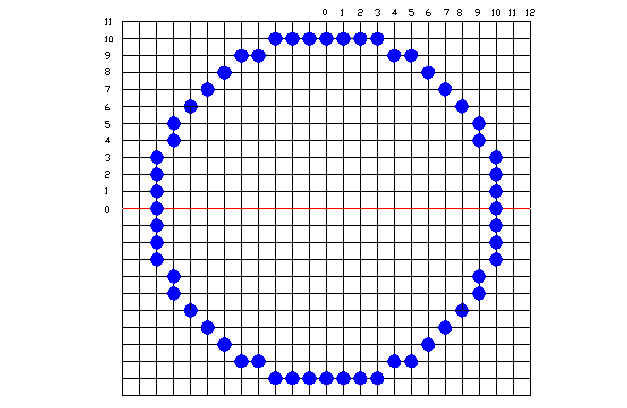
1. Korak
Zapišemo začetni točki:
- koordinati središča kroga (h,k)
- središče kroga in radij (x,y)=(0,r)
in izračunamo začetno vrednost:
d=3-2*r

2. Korak
Če je vrednost x enaka y potem STOP.

3. Korak
Določitev lokacije naslednje točke na krožnici:

- če je d<0 potem sledi:
d_i+1 = d_i + 4 * x_i + 6
(x_i+1,y_i+1)

- če je d>=0 potem sledi:
d_i+1 = d_i + 4 * (x_i - y_i) + 10
(x_i+1,y_i-1)

4. Korak
Izrišemo osem točk, najdenih po simetriji glede na središče koordinatnega sistema (h,k) in središče kroga (x,y):
Plot(x+h, y+k)                    Plot(-x+h, -y+k)
Plot(y+h, x+k)                    Plot(-y+h, -x+k)
Plot(-y+h, x+k)                   Plot(y+h, -x+k)
Plot(-x+h, y+k)                   Plot(x+h, -y+k)

5. Korak
Vrni se na korak 2.

PPM format

Spodaj je predstavljen primer zelo majhne rastrske datoteke širine 3 točk in višine 2 točk, ki določa le črno - bele točke.

V prvi vrstici je magični znak P3, ki je potreben za razpoznavo tipa datoteke. Opciji sta le P3 in P6. Znak P3 pove,da gre za ASCII obliko, kakršna je tudi naša, P6 pa bi predstavljal binarno verzijo.

V drugi vrstici sta podatka za širino in višino slike ( prvi predstavlja širino 3 točk, drugi pa višino 2 točk ). Skupaj torej 6 točk oz pixlov.

V naslednji vrstici je vrednost za maximalno velikost svetlosti, ki je v našem primeru v mejah od 0 do 15. Vrednost 0 predstavlja popolnoma temno, 15 pa povsem svetlo barvo. Vmesne vrednosti predstavljajo sivinske barve na prehodu iz bele v črno in obratno. Za maximalno velikost svetlosti bi lahko izbrali tudi število 255 ; v tem primeru bi števila tekla od 0 do 255.

Naslednje vrstice predstavljajo bazo podatkov o barvi posameznega pixla. Za vsako točko se določijo tri števila in sicer število za rdečo, zeleno in modro barvo.
Tako npr. ( 255 0 0 ) predstavlja rdečo, ( 0 255 0 ) zeleno in ( 0 0 255 ) modro barvo. Z različnimi vrednostmi znotraj enega pixla pa dobimo vmesne barve.

V splošnem se PPM format uporablja za barvne rastrske datoteke, vendar se v definiciji omejimo le na črno - bele. Tako se zapis poenostavi in pixel zapišemo s tremi enakimi števili. Črna barva je predstavljena kot ( 0 0 0 ), bela pa kot ( 15 15 15 ). Rastrska slika se začne sestavljati v levem zgornjem kotu in se zapolnjuje tako kot si sledijo števila. Če v datoteko pišemo komentarje, jih moramo predznačiti z #, da jih prevajalnik preskoči oziroma ignorira.

Antialiasing

Kot lahko vidimo je črta ali krožnica narisana po Bresenham-ovem "stopničasta". To delno odpravimo z antialiasingom oziroma filtriranjem. Vsak pixel ima določeno barvno vrednost in glede na njemu najbližje mu izračunamo povprečno vrednost glede na njih. Tako dobimo prelivanje barve črte v barvo podlage in tako izgleda črta oziroma krožnica zglajena.
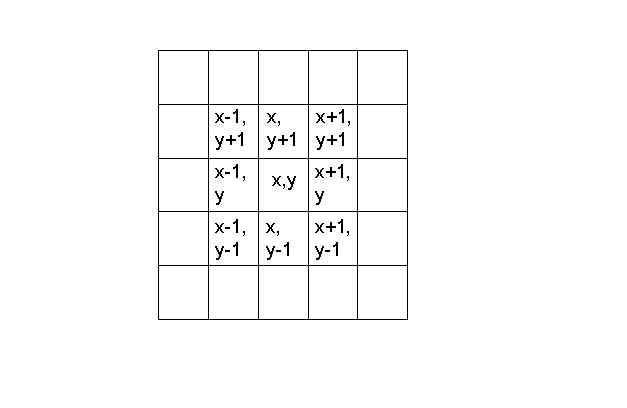
Vrednost i-tega pixla:
V(x,y)=[v(x,y)+v(x-1,y+1)+v(x,y+1)+v(x+1,y+1)+v(x-1,y)+v(x+1,y)+v(x-1,y-1)+v(x,y-1)+v(x+1,y-1)]/9

Primeri izrisa ppm datoteke glede na različne barve črt in podlage

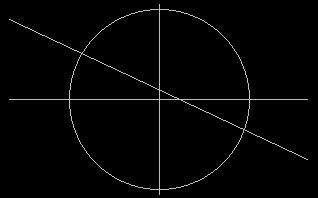
Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

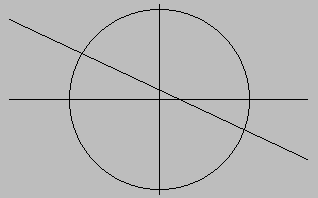
Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

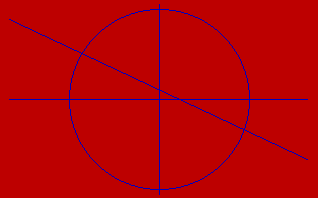
Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

Primer izrisa kroga in črte pred izvedbo antialiasinga         Primer izrisa kroga in črte po izvedbi antialiasinga

Primer izrisa dela kroga pred izvedbo antialiasinga            Primer izrisa dela kroga po izvedbi antialiasinga

Koda programa: program.pas

Program: program.exe

Literatura

[1]    Computer Graphics, SE, Hearn D., Baker M., 1996
[2]    Computer Graphics, Roy A. Plastock, Gordon Kalley, 1986
[3]    Computer Graphics, Principles And Practice, SE, Foley, 1990
[4]    Uvod v HTML, Programiranje spletnih strani, Hribar P., 1999