Rotacija 3D lika z uporabo kvaternionov

Vaja pri predmetu Racunalnisko Podprto Konstruiranje

Univerza v Ljubljani
Fakulteta za strojnistvo
Laboratorij za CAD - LECAD
Univerzitetni studij
Predavatelj: izr.prof. Dr. Joze Duhovnik, dipl.ing.
Asistent: Mag. Leon Kos, dipl.ing.
 
 
Izdelal: Saso Carli

Kazalo vsebine:

Abstract

 This work represent rotation 3D model by using quaternions. For rotation is used program language FORTRAN and for visualisation is used PHIGS library. 3D model is cuted 4 edge pyramid.

PROGRAM 1 : To perform rotation you must define starting vector and ending vector. Then the program solve the angle of rotation and rotate model from vector 1 to vector 2.
Problem is when angle of rotation is 0 or nPi becouse the model have no order in which directon must be rotated. To solve this problem I define :

where vector1(s1, s2, s3) and  vector2(e1, e2, e3).

PROGRAM 2 : This program also perform rotation by using quaternions. In this program you must define vector and angle of rotation. In this case I don't have any problem with singularity.
 

Uvod

Vaja predstavlja rotacijo lika s pomocjo kvaternionov. Izdelan je program, ki mrezni model, popisan v prostoru, zavrti iz enega polozaja v drugi z uporabo kvaternionov. Izris modela je z uporabo knjiznice PHIGS.

Interpolacija orientacije naj bi se izvedla indirektno z interpolacijo kotov in ne s transformacijo matrik. V dveh dimenzijah imamo samo en kot zato je vrtenje
enostavno. V treh dimenzijah pa imamo tri kote in s tem vrtenje krogle. Interpolacija je zato bolj zahtevna za prikaz.

Definicija

Kvaternioni so sestavljeni iz treh imaginarnih velcin i, j in k in skalarnega dela a

Pravila za sestavljanje imaginarnih velicin so naslednja:
 

 

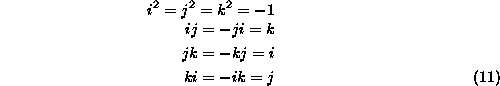
Lastnosti kvaternionov

Produkt kvaternionov ni komutativen. Kvaternioni se lahko razdelijo na skalarni in vektorski del:

V vektorski notaciji lahko zapisemo produkt dvek kvaternionov kot:


 

Enotski kvaternion
 

Enotski kvaternion podan z

za enotski vektor   je ekvivalenten rotaviji za  okoli osi definirani z .   je ekvivalenten   ko ga interpretiramo kot orientacijo.

Kvaternioni imajo tudi konjugate:  . Norma kvaterniona je definirana z

Rotacija in kvaternioni

Tocke v prostoru so lahko predstavljene s kvaternioni, ce imajo nicni skalarni del. Tocka P je predstavljena kot:


 

Rotacija tocke P je definirana z 

Za enotske kvaternione je inverz enak konjugatu.
 

Prednosti kvaternionov

 1. Za veliko aplikacij je neodvisna definicija osi zavrtitve in kota primerna.
 2. Definicija orientacije s kvaternionom je neodvisna od koordinatnega sistema in izotropna.
 3. Krozna interpolacija kvaternionov daje boljse rezultate kot Eulerjevi koti.
 

Interpolacija s kvaternioni
 
 

    Za interpolacijo dveh orientacij lahko uporabimo linearno interpolacijo vseh velicin (ga smatramo kot
    stiridimenzionalni vektor). Zal pa vmesni kvaternioni ne bi imeli enotske norme. Kotna hitrost ne bi bila
    konstantna tudi ce bi renormalizirali.
      Za interpolacijo dveh orientacij lahk ouporabimo krozno interpolacijo tako, da uporabimo kvaternione kot
    vektorje.

    Kot med dvema kvaternionoma je

 
 

    Za dani parameter   je kvaternion zavrtitve s krozno interpolacijo podan kot

 
 

Naloga.

Izdelati je potrebno program, ki bo mrezni model popisan v prostoru zavrtel iz enega polozaja v drugi z uporabo
krozne interpolacije s kvaternioni. Potrebno je resiti tudi problem singularnosti pri  in  . Izris 3D
modela in vmesnih stopenj z uporabo knjiznice PHIGS ali OPEN GL.
 

Kvaternioni

Kvaternioni so razssirjena kompleksna stevila. Kvaternione lahko predstavim na vec nacinov:
q = w + xi + yj + zk = [x y z w] = (s, v)
s = w
v = [x y z]
q´ = w - xi - yj - zk
||q|| = SQRT ( q * q´ ) = SQRT (w^2 + x^2 + y^2 + z^2 )

Znacilnosti kvaternionov

 

Osnove rotacije s kvaternioni

Racunam rotacijo okoli enotnega vektorja u za kot ß. Kvaternion, ki popisuje to rotacijo je
 
  q = (s, v) = (cos (ß/2), u sin(ß/2))
s = cos (ß/2)
v = u sin(ß/2) = x sin(ß/2), y sin(ß/2), z sin(ß/2)

Tocko p v prostoru predstavim s kvaternionom P = ( 0, p). Zeljeno rotacijo tocke p izracunam s enacbo

  P = ( 0, p) = [ Xp Yp Zp 0 ]
P(rotirano) = q P q^(-1)

Matricni zapis rotacije

q = [ Xq Yq Zq Wq]
q^(-1) = q´ = [-Xq -Yq -Zq Wq]
q P q´ = P Qrot

Qrot = mat(4,4)
 
 

w^2 + x^2 - y^2 - z^2 
2xy + 2wz  
2xz - 2wy 
0 
2xy - 2wz 
w^2 - x^2 + y^2 - z^2 
2yz + 2wx 
0 
2xz + 2wy 
2yz - 2wx 
w^2 - x^2 - y^2 + z^2 
0 
0 
0 
0 
w^2 + x^2 + y^2 + z^2 
 

S to matriko lahko zapisemo P(rotirano) drugace

 
  P(rotirano) = P Qrot = [ Xp Yp Zp 0 ] Qrot

PHIGS knjiznica

Knjiznica omogoca risanje in prikaz na izhodnih enotah. Navodilo za risanje s pomocjo PHIGS knjiznice se nahaja na spletni strani http://www.lecad.uni-lj.si/documents/phigsd/lib-users.html
 

Postopek izdelave programa

Postopek je nazorno opisan ze med programiranjem, zato si lahko ogledate kar datoteko rotk.txt. Izdelal pa sem se drug program, kjer je potrebno podati vektor 1 in nato vektor 2, nato program rotira lik od V1 do V2 in nam na koncu se izpise kot zasuka. Program je napisan v datoteki vrk21.txt
 

Program

Program je izdelan s programskim jezikom Fortran in z uporabo PHIGS knjiznice. Grafika je predstavljena za 21"/1280*1024 in 15"/1024*768. Maksimalna dolzina stranice ali visine 4-strane presekane piramide naj bi bila 100 enot.
Rotacija je animirana tako, da podamo zasuk do koncnega stanja, nato pa se podamo stevilo vmesnih stopenj do koncnega stanja.

Program 2 za 21"/1280*1024 in 15"/1024*768
 

PROGRAM 1:
1.Podaj vrednosti enotskega smernega vek. u=x,y,z!
Podamo koordinate tocke smernega vektorja, ki ima izhodisce v koordinatenemu izhodiscu (0,0,0)

2.Podaj vrednosti kota zasuka theta v stopinjah!
Podamo kot celotnega zasuka. Kot se poda v stopinjah. Rotacija se izvaja okoli vektorja u

3.Velikost spodnje stranice a 4-str. 3D lika!

4.Velikost zgornje stranice b 4-str. 3D lika!

5.Visina 4-str. 3D lika!

6.Stevilo vmesnih stopenj do koncnega polozaja!
Podamo stevilo vmesnih stopenj, ki naj jih program narise, da pridemo do koncnega stanja.
 

PROGRAM 2:
1.Podaj vrednosti zacetnega enotskega smernega vek. V1=x,y,z!
Podamo koordinate tocke smernega vektorja, ki ima izhodisce v koordinatenemu izhodiscu (0,0,0)

2.Podaj vrednosti  koncnega enotskega smernega vek. V2=x,y,z!
Podamo koordinate tocke smernega vektorja, ki ima izhodisce v koordinatenemu izhodiscu (0,0,0)

3.Velikost spodnje stranice a 4-str. 3D lika!

4.Velikost zgornje stranice b 4-str. 3D lika!

5.Visina 4-str. 3D lika!

6.Stevilo vmesnih stopenj do koncnega polozaja!
Podamo stevilo vmesnih stopenj, ki naj jih program narise, da pridemo do koncnega stanja.
 
Program zahteva tudi tocno definiranje osi rotacije pri kotih rotacije 0 in 180 stopinj. V programu sem definiral osi rotacije za naslednje primere, ko so koordinate enotskega vektorja V1[s1, s2, s3] v naslednjem razmerju z koordinatami enotskega vektorja V2[e1,e2,e3]:

1. s1=-e1        rotacija okoli Z osi
2. s2=-e2        rotacija okoli Z osi
3. s3=-e3        rotacija okoli X osi
4. s1=e1         rotacija okoli X osi
5. s2=e2         rotacija okoli Y osi
6. s3=e3         rotacija okoli Z osi

Pri tem so variante pod zaporednimi stevili tudi prioritetno uvrscene. Npr. ce imamo enotski vektor V1[2, 4, 0]
in V2[1, 4, 0] bo rotacija okoli X osi saj je koordinata s3=-e3.
 
Prevajalnik PHIGS knjiznice DJGPP je mogoce dobiti na strezniku ftp.lecad.uni-lj.si na podrocju /pub/vaje/install. Program je potrebno razsiriti na direktorij c:\djgpp, nato pa pognati datoteko POT.BAT. Tako je vse nared za pogon izvr¹nih programov z uporabo PHIGS knjiznice.

 
 4-strana presekana piramida
 

E-mail : [email protected] 
NASLOV:
Saso Carli
Rozna 9
5280 Idrija
Slovenija
+386 65 71-089, +386 65 73-554