

![]()
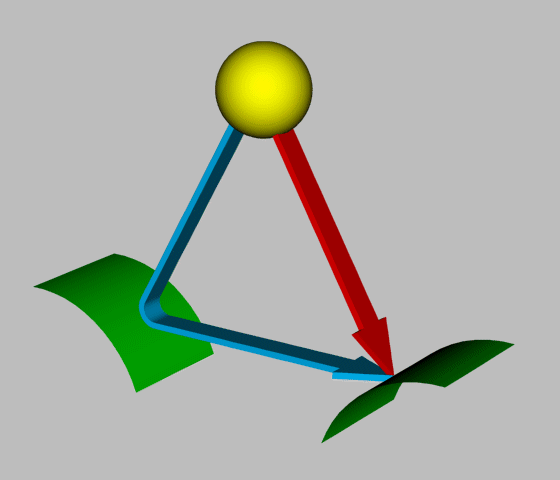
Osnovna enačba odboja svetlobe je shematsko prikazana na spodnji skici
(Slika 2.).
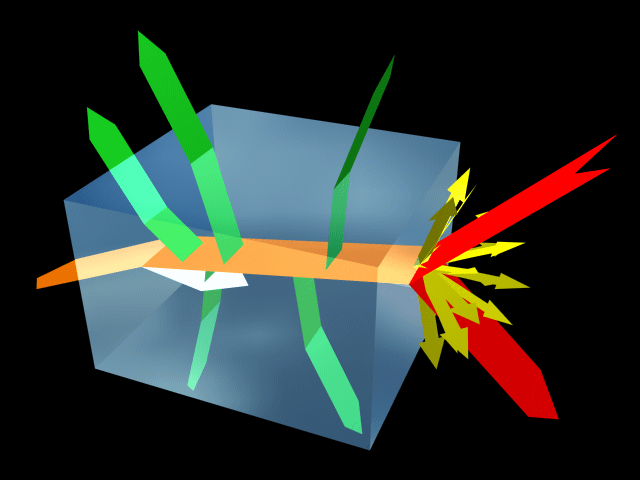
Slika 2.(Zrcalno odbita svetloba,
razpršena svetloba, fluorescenca,
notranji odboj svetlobe, lomljena
svetloba)
Intenziteta (svetlost ali moč) svetlobe odbite od površine in njena
valovna dolžina (barva svetlobe) je odvisna od valovne dolžine vpadne svetlobe,
kota pod katerim je osvetljena površina, od hrapavosti površine in električnih
lastnosti materiala površine (permanenca, permabilnost in prevodnost).
Zelo natančna povezava med vsemi vplivi je zelo kompleksna. Ista površina
je lahko za določene valovne dolžine gladka in za druge hrapava. Lahko
pa je površina pri isti valovni dolžini za različne kote osvetlitve različno
hrapava. Primer je bleščanje ceste pri sončnem zahodu, ko je kot osvetlitve
majhen, med tem ko opoldan ni bleščanja (velik kot osvetlitve).

Slika 3.(N - normala površine, L - vektor luči, V
- vektor očesa)
BDRF funkcija je podana kot razmerje med z intenziteto odbite svetlobe in energijo vpadne svetlobe :

Zveza med energijo vpadne svetlobe in vpadno osvetljenostjo površine (inteziteta) :
![]()
Za uporabo v računalniški grafiki je BDRF funkcija razdeljena na tri komponente :
![]()
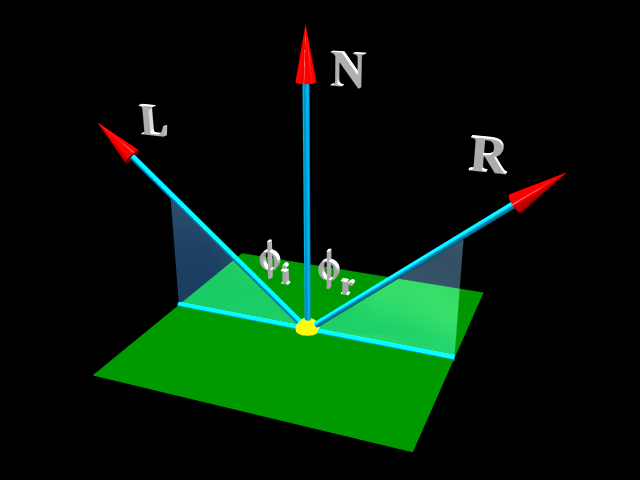
Slika 4.(Zrcalno odbita svetloba - a specular contribution)
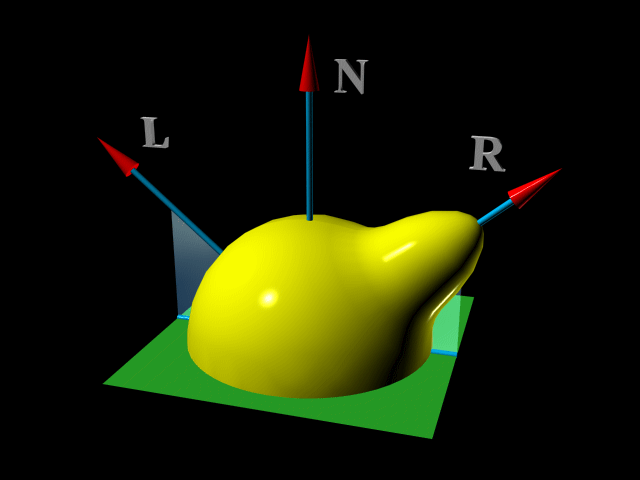
Slika 5.(Usmerjeno razpršena svetloba - a directional diffuse contribution)

Slika 6.(Idelano razpršena svetloba - an ideal diffuse contribution)
Svetlobni model Phong je linearna kombinacija treh komponent :
Ii je moč točkastega izvora svetlobe. Theta je kot med normalo površine v opazovani točki in daljico med opazovano točko in izvorom svetlobe. kd je empirični koeficient odvisen od valovne dolžine svetlobe. Zgornjo enačbo lahko zapišemo v vektorski obliki :
![]()
Kjer je L vektor luči in N normala površine. Oba vektorja sta enotska (dolžina je 1). Če imamo večje število izvorov svetlobe, se enačba glasi :
![]()
Kjer je Ln smerni vektor n-tega svetlobnega izvora
do točke na površini.

Slika 7.(Določitev intenzitete razpršene svetlobe)
Odblesk je funkcija kota omega, ki je kot med smerjo gledanja in smerjo zrcalnega odboja svetlobe (Slika 8.) :
![]()

Slika 8.(Določitev intenzitete zrcalno odbite svetlobe)
Indeks n simulira hrapavost površine. Za popolno ogledalo je indeks n neskončno velik in odbita svetloba je v smeri zrcalnega odboja. Gladko površino ponazorimo z večjim indeksom n, s tem je velikost odbleska manjša. Nasprotno je s hrapavo površino, pri kateri je n majhen in zato velikost odbleska večja. Odblesek je slika izvora svetlobe na površini. Barva zrcalno odbite svetlobe je različna od barve razpršene svetlobe. Predpostavljeno je, da ima zrcalno odbita svetloba barvo izvora svetlobe. V primeru zelene površine in belega izvora svetlobe je barva razpršene svetlobe zelena, barva odbleska pa bela. Delovanje svetlobnega modela Phong temelji le na omega in n, zato ni dvosmernega pojava. Vrednosti kotov (fi,theta) niso v odvisnosti od materiala površine. To je ena od glavnih pomanjkljivosti modela Phong.
Svetlobni model Phong ne upošteva globalne osvetlitve, zato je komponentama razpršene in zrcalno odbite svetlobe dodana še komponenta ambienta. Ker v glavnem za osvetlitev objektov uporabljamo točkovni izvor svetlobe, bi bile površine, ki niso vidne s strani izvora svetlobe, obarvane črno. S tem bi dobili učinek scene v temi, ki je osvetljena z bliskavico. Ambientna komponenta je konstanta, ki delno upošteva globalno osvetlitev.
![]()
Če seštejemo vse tri komponente svetlobe (razpršena, zrcalno odbita svetloba in svetloba okolice) dobimo enačbo svetlobenega modela Phong :
![]()
V nekaterih primerih je pri lokalnih svetlobnih modelih upoštevana oddaljenost točk na površini od izvora svetlobe. S tem dobimo pogoj, da se spreminja svetlobna intenziteta kot funkcija oddaljenosti površine od izvora svetlobe. Ta pogoj preprečuje, da bi površina enake orientacije (ravnina) in z različno oddaljenostjo od izvora svetlobe, bila osvetljena po celotni površini z enako intenziteto. Za izvore svetlobe smatramo, da so postavljeni na neskončni oddaljenosti od površine. S tem smo dobili svetlobo z vzporednimi žarki, zato ni potrebno upoštevati obliko svetlobnega snopa (stožec). Zaradi te predpostavke uporabimo razdaljo med točko pogleda in površino, ne pa razdaljo med izvorom svetlobe in površino. Enačba svetlobnega modela ima sedaj obliko :
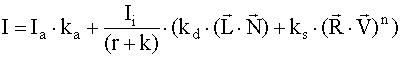

To je potrebna orientacija površine, da se svetloba odbije v smeri vektorja
V. Kot med R in V je dvakrat večji od kota med N
in H, kar kompenziramo s spreminjanjem parametra n. Uporaba skalarnega
produkta (N*H) namesto (R*V) pri isti vrednosti
n, razširi odblesek na večje območje površine.
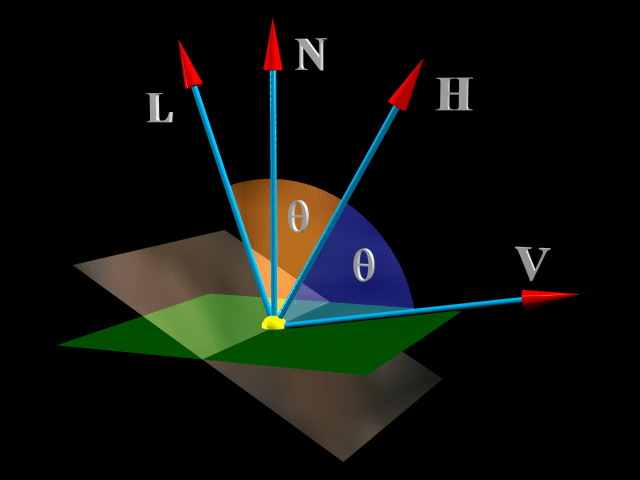
Slika 9.(Definicija vektorja H)
Sedaj se enačba svetlobnega modela Phong glasi :

Intenziteta svetlobe je sedaj funkcija samo normale površine N.
Če sta vektorja L in V konstantna, potem je konstanten tudi
vektor H. S postavitvijo izvora svetlobe v neskončnost pridemo do
dveh sklepov. Prvič, ni variranja v barvi osenčenih ravnih površin (zanemarimo
efekt faktorja oddaljenosti izvora svetlobe od površine (r+k)), ker je
L konstanten in N se ne spreminja po površini. Drugič, oblika
odbleska se spreminja.

Tri enačbe združimo v eno samo :
![]()
Za zahtevnešo uporabo je tri-barvni pristop mešanja osnovnih barv preveč grob, ker ne da dovolj realnega rezultata.
Program je napisan v programskem jeziku FORTRAN. V tem programskem jeziku
je delo z grafiko zelo težavno, zato je rezultat zapisan v datoteki. Uporabljen
je grafični format datoteke, ki omogoča zapis rastrske slike v ASCII formatu
(Portable PixMap file format - PPM).

Primer (Majhna rasterska slika velikosti 4x4 točk)
Zapis zgornje rastrske slike velikosti 4x4 točk v PPM formatu (datoteka : primer.ppm) :
P3
# primer.ppm
4 4
255
200 0 0 255 0
0 255 0 0 255 0 0
0 0 255 200 0 0
255 0 0 255 0 0
0 0 255 0 0 255
200 0 0 255 0 0
0 0 200 0 0 255
0 0 255 200 0 0
Prva vrstica ima magični znak P3, ki je potreben za razpoznavo tipa
datoteke. V drugi vrstici je označba 4 točk široke in 4 točk visoke slike,
kar je skupaj 16 točk (pikslov). ©tevilo 255 označuje maksimalno vrednost
svetlosti v sliki, ki je v razponu od 0 do 255. Za vsako točko se določi
trojka števil za rdečo, zeleno in modro barvo (RGB), zato sledi 3*16=48
števil. Črna barva ima vrednost (0 0 0), bela pa (255 255 255). Rastrska
slika se začne sestavljati v zgornjem levem kotu v smeri branja. ©tevila
so ločena s presledki (prazen prostor). V okolju X-Windows lahko gledamo
PPM datoteke s programom XV, v okolju MS-windows pa s programom Paint Shop
Pro.
Izvor svetlobe in opazovalca postavimo na neskončno oddaljenostjo od krogle, tako da sta vektor luči L in vektor pogleda V konstantna za celotno območje slike. S tem je konstanten tudi vektor H. Geometrijski model je pravokotna projekcija (ne upoštevamo realne projekcije). Krogle so postavljene na xy-ravnino. Pogled je v smeri z-osi in zato pravokoten na ravnino v kateri ležijo krogle. Osvetlitev je iz smeri (1,1,1) in je enaka za vse krogle. Odločili smo se za lokalni svetlobni model, ki upošteva oddaljenost luči od točke na površini. Oddaljenost in moč luči je za vse krogle enaka. Za vse krogle je konstantna intenziteta ambientne svetlobe. Radij krogel bomo določili glede na zahtevano velikost risbe.
Ker je pogled prvokoten na xy-ravnino in projekcija pravokotna, lahko koordinate točk na sferah uporabimo za koordinate (indekse) pixel-ov. Računanje bo zato potekalo s celoštevilskimi vrednostmi pixel-ov. Koordinata z se na sliki ne vidi. Zaradi prej omenjenih poenostavitev in predpostavk, je takšen program strogo namemeben. Z njim je mogoč le izris krogel. Varirati je možno parametre svetlobenega modela, velikost risbe, z dodatnim predhodnim računanjem lahko spremenimo smer osvetlitve in število krogel. Sama uporaba programskega jezika FORTRAN ne omogoča hitre uporabe programa zaradi vmesnega zapisovanja PPM datoteke, katere velikost je zelo velika v primerjavi z ostalimi grafičnimi formati (nekaj MB za 800x600 veliko risbo).
Vse konstante izračunamo predhodno tako, da enačba intenzitete svetlobe
za posamezno barvo (RGB) ne preseže vrednosti 1. S tem smo posredno normirali
vrednosti intenzitete svetlobe na vrednost enako ali manjšo 1.
V prvem koraku določimo velikost risbe v pixel-ih in vse spremenljivke,
ki so z njo povezane (radij, koordinate središča krogle). S predhodno definirano
tro-dimenzionalno matriko slike zapišemo ozadje risbe. Matrika slike je
kvader razdeljen na tri rezine. Vsaka rezina je namenjena zapisovanju svetlosti
(med 0 in 255) za posamezno osnovno barvo (RGB). ©irina risbe je enaka
številu polj po širini rezine (enako velja za višino). Velikost matrike
slike je :
![]()
Glavni program deluje tako, da za vsako kroglo posebej določi vrednost vseh pixel-ov. Njihove vrednosti zapišemo v matriko slike. Točke na krogli, katere središče leži v koordinatnem izhodišču, določimo iz pogoja :
![]()
z-koordinato določimo iz enačbe za kroglo :
![]()
Normalo določimo iz vektorja, ki ga določajo koordinate točke, ki leži na krogli. Potrebno je samo normirati normalni vektor na dolžino 1 :

Sledi izračun skalarnega produkta (L*N) in kontrola, če je točka osvetljena. Točka ni osvetljena, če je skalarni produkt enak ali manjši od nič (kot je večji od 90°) :
![]()
![]()
Pri izpolnjenemu pogoju osvetljenosti določimo oddaljenost točke od luči :
![]()
Izračun skalarnega produkta (N*H) :
![]()
Če točka ni osvetljena, potem je vrednost pixel-a enaka intenziteti svetlobe ambienta pomnožena z 255 (Phong.for), v nasprotem primeru določimo intenziteto svetlobe po enačbi :

Vrednost barve pixel-a zapišemo v matriko risbe, pri tem upoštevamo
koordinate središča krogle. Ko program opravi vse korake, zapiše datoteko
Phong.dat v predpisani obliki. V Explorer-ju datoteko preimenujemo v Phong.ppm
in pogledamo z programom Paint Shop Pro.
Parameter širine odbleska n :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
