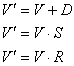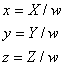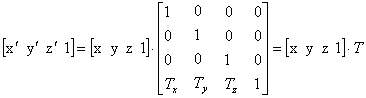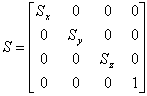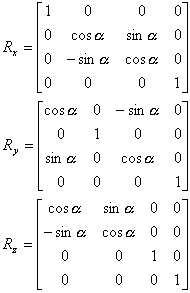RPK - seminar
Tomaž Skubic
RAZTEGNJENE PLOSKVE
KAZALO
Raztegnjene ploskve so ploskve, ki nastanejo na podlagi osnovne
krivulje in krivulje raztega. Osnovna krivulja je lahko poljubna, torej je lahko sklenjena
ali razklenjena. Krivulja raztega je ponavadi razklenjena krivulja. V laboratoriju LECAD
smo že uporabljali programski paket I-DEAS, ki v ta namen kreiranja površin uporablja
opciji 'extrude' in 'loft'. Na zaslonu prikažemo ploskev torej s povezavo točk, ki
tvorijo ploskvice, množica ploskvic pa skupaj tvori želeno ploskev.
The task of my assigment was to generate surfaces. This surfaces
were generated from basic curves, which were extruded in defined direction (the curve of
extension). The program has to read the input file which containes the data of basic and
extension curve. The program transforms each vertex and links all vertex into a net. The
net represents the surface. The output file so containes the data of vertex and polyline
in DXF format.
Program mora zadostiti naslednjim zahtevam:
- Branje vhodnih podatkov iz vhodne datoteke,
- Prikaz modela s knjižnico PHIGS v poljubni orientaciji,
- Zapis ploskve v formatu DXF ali Inventor
Vhodna datoteka naj vsebuje naslednje podatke:
- Osnovno krivuljo,
- Krivuljo raztega,
- Število delitev v smeri osnovne krivulje,
- Število delitev v smeri raztezne krivulje,
- Pogled na krivuljo (koti rotacij v prostoru);
Oblika zapisa osnovne krivulje in krivulje raztega
je poljubna. Odločil sem se za prikaz poljubne krivulje z množico točk. Vhodna datoteka
torej vsebuje množico točk, ki popisuje osnovno krivuljo, množico točk, ki popisuje
krivuljo raztega, dodani pa so še pomožni podatki, ki služijo za ustrezen prikaz
nastale ploskve (translacija v x-smeri, translacija v y-smeri, translacija v z-smeri,
rotacija okoli x-osi, rotacija okoli y-osi, rotacija okoli z-osi, skaliranje).
| int | stevilo tock osnovne krivulje(i) |
| float float float | koordinate prve tocke(x,y,z) |
| float float float | koordinate druge tocke(x,y,z) |
| . | . |
| . | . |
| . | . |
| int | stevilo tock raztezne krivulje(j) |
| float float float | koordinate prve tocke(x,y,z) |
| float float float | koordinate druge tocke(x,y,z) |
| . | . |
| . | . |
| . | . |
| float float float | translacija v x,y in z smeri |
| float | rotacija v x-smeri |
| float | rotacija v y-smeri |
| float | rotacija v z-smeri |
| float | skaliranje |
Slika 1: oblika vhodne datoteke
Da bi uporabnik imel vtis, da se objekti nahajajo v
prostoru, je potrebno že pred manipulacijo z objekti le-te rotirati npr. v izometrični
položaj. Da bo položaj objektov v prostoru razviden na zaslonu, naj se izrišejo in
označijo tudi koordinatne osi. Nadalje pa mora biti omogočeno, da objekte uporabnik
prestavlja (translacija), vrti (rotacija) in povečuje/zmanjšuje (skaliranje). Te
operacije se da matematično popisati z ustreznimi matrikami, s katerimi učinkujemo na
naše objekte. Pri tem gre za množenje matrik s koordinatami vseh točk objekta.
Pri uporabi matrik točko V transformiramo s pomočjo translacije,
skaliranja in rotacije:
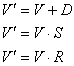
Slika 2: transformacije točke
kjer je D vektor translacije, S in R pa matriki
skaliranja in rotacije.
Te tri operacije so najpogostejše linearne transformacije v
računalniški grafiki, ki jih uporabljamo v homogenih koordinatah. V homogenih
koordinatah je točka V(x, y, z) predstavljena kot V(x, y, z, w). Predstavitev v
tri-dimenzionalnem kartezijevem koordinatnem sistemu je naslednja:
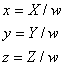
Slika 3: zapis točke v kartezijevem koordinatnem sistemu
V računalniški grafiki je w vedno enak 1, zato je
predstavitveni vektor točke [x y z 1]. Translacija je zdaj lahko tretirana kot matrično
množenje:
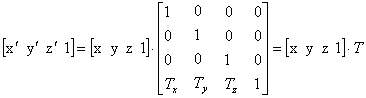
Slika 4: zapis translacije točke v matrični obliki
Transformacijo končamo s skaliranjem in rotiranjem:
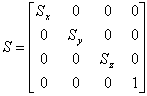
Slika 5: matrika skaliranja
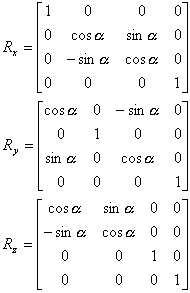
Slika 6: matrika rotacij
Skupna transformacijska matrika ima torej obliko:

Slika 7: transformacijska matrika
- Vključimo potrebna zaglavja,
- Definiramo vse spremenljivke,
- Definiramo točke koordinatnega sistema,
- Definiramo zaslonske koordinate okvirja,
- Definiramo spremenljivke v grafični knjižnici PHIGS,
- Program poskrbi, da se ustrezno pripravljeni podatki v datoteki prečitajo v spominska
polja,
- Nastavimo transformacijsko matriko, ki transformira točke osnovne krivulje in točke
raztezne krivulje,
- Izračunamo razdalje posameznih točk osnovne krivulje do prve točke osnovne krivulje
(vektor premika),
- Vektorje premikov prenesemo na vsako posamezno točko raztezne krivulje (dobimo mrežo
točk ),
- Transformiramo koordinatni sistem (ker služi samo za prikaz rotacij, mora biti
translacija zadnja operacija, da je koordinatni sistem vedno na istem mestu),
- Odpremo grafično knjižnico PHIGS,
- Določimo meje splošnega koordinatnega sistema,
- Nastavimo uporabniški koordinatni sistem,
- Nastavimo zaslonske koordinate,
- Izrišemo koordinatni sistem,
- Izrišemo raztezne krivulje,
- Izrišemo osnovne (vmesne) krivulje,
- Zapis točk in črt raztezne in osnovne krivulje v DXF formatu;
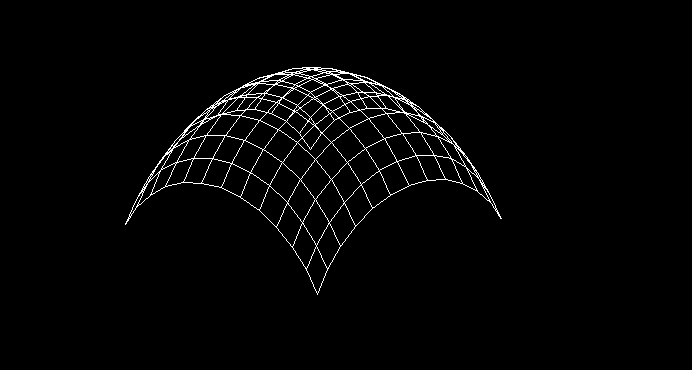
Slika 8: prvi primer delovanja programa
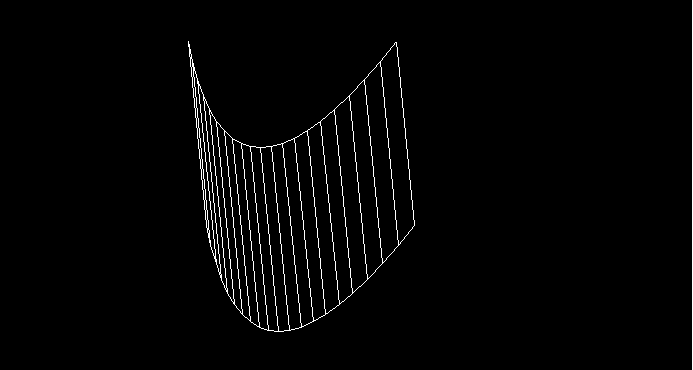
Slika 9: drugi primer delovanja programa
| Matjaz Prtenjak: | C++ za velike in male |
| Alan Watt: | Fundamentals of Three-Dimensional Computer Graphics |
| Laboratorij LECAD: | Emulacija knjižnice PHIGS |