Laboratorij za Racalnisko Podprto Konstruiranje LECAD
Univerzitetni studij Predavatelj: prof. dr.Joze Duhovnik, dipl.ing.
Asistent: mag. Leon Kos, dipl.ing.
Avtor : Miha Janezic
KAZALO
Uvod - Inkrementalne tehnike sencenja
Gouraud-ova tehnika sencenja - Teoreticne osnove
This article deals with theory of reflection and shading in computer graphics, especialy with theory of Incremental - Gouraud shading method. This theory is used in program Gouraud.exe which can be found on ftp server: ftp.lecad.uni-lj.si.
Inkrementalne oziroma interpolacijske tehnike sencenja delujejo tako, da enostavne odbojne modele razdelijo na mnogokotnike, izracunajo intenzitete na vozliscih, potem pa z interpolacijo dobijo se vrednosti za notranje tocke mnogokotnikov. Vrednotenje notranjih tock se izvedede z enostavno metodo "skenirne crte (scan line)", tako dobljene sheme je mogoce enostavno vgraditi v metode za odstranjevanje skritih povrsin.
V praksi sta najpogostejsi dve metodi inkrementalnega sencenja; Gouraud-ova interpolacija (Gouraud 1971) in Phong-ova interpolacija (Phong 1975). S Phong-ovo interpolacijo dobimo tocnejse osvetlitve in sijaje in je bolj priljubljena. Gouraurd-ova metoda je primernejsa za primere, kjer se zadovoljimo le z difuzno komponento svetlobe, pogosto pa se uporablja tudi za predogled slik pred koncnim sencenjem.
Phong-ova metoda je potratnejsa in se podreja prvemu zakonu racunalniske grafike, ki pravi, da porabljen procesorski cas eksponentno narasca s kakovostjo slike.Gouraud-ova metoda sencenja pa je postala nekaksen standard za graficno strojno opremo, kjer pa se v zadnjem casu pojavlja tudi Phong-ova metoda. Ta trend se izraza tudi v standardu PHIGS+, ki vkljucuje obe tehniki sencenja.
Vecno vprasanje, ki se pojavlja je kako narediti preracun sencenja cim hitrejsi. Phong-ova tehnika sencenja lahko porabi nad 50% skupnega procesorskega casa renderiranja, zato je cim hitrejsi preracun sencenja prav tako pomemben kot kakovost slike, se posebej kadar se ukvarjamo s tri dimenzionlnimi animacijami.
Pri interpolacijskih tehnikah sencenja je potrebno opozoriti se na en problem, to je koncna vidljivost mnogokotnikov. Meje mnogokotnikov naj po koncnem sencenju ne bi bile vidne poleg tega pa se mora ohraniti originalna oblika povrsine, ki smo jo sencili z mnogokotniki.
Gouradova tehnika sencenja je prva, ki namesto konstantnega sencenja poligonov uporablja bilinearno interpolacijo intenzitete. Je enostavna in hitra tehnika, ki pa ne odpravi v popolnosti vidnosti robov mnogokotnikov. Poleg tega se pojavijo tudi Mach-ovi robovi (Mach banding), kar pomeni da majhne linearne spremembe intenzitete svetlobe preko povrsine pravokotnika povzrocijo da opazovalcev vid zazna rob kot svetlo crto. Razlaga za to je obcutljivost clovekovega vida na drugi odvod osvetljenosti, ki ga imamo zaradi potrebe po natancnem zaznavanju robov.

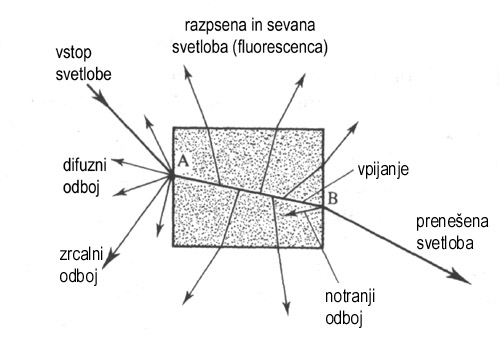
Slika 1 - Zakon odboja svetlobe
Enostavno lahko zakon odboja ponazorimo z zgornjo skico oziroma ga zapisemo z enacbo:
Svetloba, ki prileti na povrsino = (odbita + razprsena + vpita + prenesena) svetloba
Racunalniska grafika se v vecini primerov posluzuje le odbojne in vcasih prenesene komponente svetlobe. Moc in valovna dolzina svetlobe sta odvisna od moci in valovne dolzine vhodne svetlobe, kota vpada svetlobe na povrsino, hrapavosti povrsine, materiala na povrsini in od elektricnih lastnosti povrsine. Natancna odvisnost je seveda zelo kompleksna.
Id = Ii*kd*cos(theta) ; 0 <= theta <=pi / 2 [enacba 1]
Slika 2 - Tri povrsine z difuznim odbojem svetlobe
Lambertov zakon lahko zapisemo tudi s skalarnim produktom:
Kjer je: N - normala povrsine, L - smerni vektor od izvora svetlobe proti tocki na povrsini.
V sencen graficni model lahko dodamo koeficient s katerim zmanjsamo moc osvetljenosti povrsine v odvisnosti od oddaljenosti povrsine od izvora svetlobe. S tem dosezemo, da so povrsine, ki imajo enako barvo in so na razlicnih oddaljenostih od vira svetlobe razlicno osvetljene. Namesto razdalje med izvorom svetlobe in povrsino pa v graficni model raje vpeljemo razdaljo med povrsino in tocko gledanja. Enacba dva tako postane:
Id = Ii*kd*(L·N)/(r+k) [enacba 3]
Kjer je r oddaljenost od tocke gledanja, k pa konstanta. Delitelj (r+k) ne izboljsa dosti koncnega izgleda sencenega objekta, zato ga v primerih ko je hitrost sencenja kljucnega pomena izpuscamo.
Na enacbi 3 pa bazira Gouraud-ova tehnika sencenja.
Gouraud-ova tehnika sencenja izhaja iz intenzitet vozlisc posameznih mnogokotnikov, ki sestavljajo senceno povrsino. Slika 3 prikazuje nacin dolocanja "vozliscnih normal". Usmerjenost normale v vozliscu je nekaksna srednja vrednost usmerjenosti normal povrsin mnogokotnikov, ki se v tem vozliscu stikajo.

Slika 3 - Princip dolocevanja vozlisnih normal
Ce predpostavimo, da je izvor svetlobe v neskoncnosti je skalarni produkt L·N po celi povrsini enega mnogokotnika konstanten. Edina spremenljivka (odvisna od polozaja na povrsini mnogokotnika) je r - razdalja do tocke gledanja. Ponavadi pa pri Gouraud-ovi tehniki sencenja zanemarimo tudi to spremenljivko. Tako lahko izracunamo vrednosti intenzitete svetlobe na vozliscih posameznega mnogokotnika in z bilinearno interpolacijo izracunamo se vrednosti intenzitete svetlobe notranjih tock mnogokotnika. Postopek Gouraud-ove tehnike sencenja je torej sledec:
Izracun intenzitete vozlisc:
Dolocitev "vozliscnih normal": 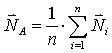 .
[enacba 4]
.
[enacba 4]
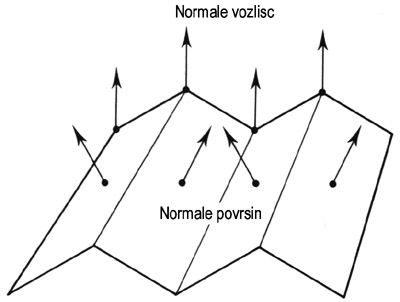
Slika 5 - Tezave z vozliscnimi normalami
Slika 5 prikazuje tezavo na katero lahko naletimo pri opisanem dolocevanju vozliscnih normal. Ce je neka povrsina lomljena simetricno bodo vse vozliscne normale enako usmerjene in povrsina bo sencena kot bi bila ravna. Tej napaki se lahko izognemo s "pametnim" mrezenjem sencenih povrsin.
Izracun vozliscne intenzitete: ![]() ,
[enacba 5]
,
[enacba 5]

Slika 4 - Oznacevanje uporabljeno v interpolacijskih enacbah
Rasterizacija in izracun intenzitete tock na robovih mnogokotnika:
Iz vozliscnih tock dolocimo tocke na robovih sencenega lika
Z uporabo spodnjih enacb izracunamo intenziteto na robovih mnogokotnika
 [enacba 6]
[enacba 6]
 [enacba 7]
[enacba 7]
Izracun intenzitete tock v notranjosti mnogokotnika
Z uporabo interpolacijske enacbe spodaj izracunamo intenziteto svetlobe v notranjih tockah
 [enacba 8]
[enacba 8]
Prikaz tock na zaslonu ali zapis v datoteko
Program deluje po zgoraj opisanem postopku, pri tem pa je upostevanih nekaj poenostavitev. Ker se s programom senci le en trikotnik, so vse vozliscne normale enake normali trikotnika. Da bi bilo vseeno mogoce cimbolje prikazati delovanje metode razdalja med izvorom svetlobe in povrsino ni neskoncna, pac pa je enotska. Tako lahko s premikanjem luci po prostoru dosezemo razlicno osvetljeno povrsino in razlicne gradiente intenzitete osvetlitve preko povrsine. Program senci tako ravninske (z=0), kot tudi prostorske trikotnike, ki pa so vselej prikazani v pravokotni projekciji.
Gouraud.exe je enostaven program napisan v jeziku C++ za operacijski sistem Windows 95/98. Po zagonu datoteke Gouraud.exe se odpre programsko okno z dvema padajocima menijema. Meni Gouraud (slika 6) je namenjen delu s programom.
Slika 6
Trikotnik sencimo na sledec nacin:

Slika 7
V vnosna polja vnesemo zeljene podatke in vnos potrdimo s klikom na gumb OK.
Vhodni podatki:

Slika 8
Ce naprimer dvignemo izvor svetlobe na z = 300:

Slika 9
Lahko vidimo, da v primeru ko izvor svetlobe odmikamo od povrsine ta postaja enakomerno obarvana. To je posledica skalarnega produkta LN v enacbi za intenziteto svetlobe, ko je luc dovolj dalec od povrsine je skalarni produkt v vsakem od ogljisc priblizno enak, s tem so tudi intenzitete svetlobe v vseh ogljiscih priblizno enake, bilinearna interpolacija intenzitete pa nam da enako vrednost intenzitet tudi za notranje tocke trikotnika.
Ce pri istem trikotniku spustimo levo ogljisce za z = -150, izvor svetlobe pa priblizamo nazaj na z = 150, opazimo podoben rezultat, le vzrok je v tem primeru drug, luc sedaj namrec sveti pravokotno na sredino trikotnika.

Slika 10
Isti efekt dobimo ce luc prestavimo na sredino trikotnika, podatki uporabljeni za naslednje sencenje so:
Situacija je sledeca:

Slika 11
Izgled sencene slike pa je:

Slika 12
Ker je osvetlitev na sredini trikotnika, poleg tega pa tudi precej blizu povrsine bi pricakovali mocnejso osvetlitev proti sredini trikotnika. Gouraud-ova metoda sencenje pa tega zaradi nacina bilinearne interpolacije ne omogoca. Moc osvetlitve vseh tock namrec izhaja iz moci osvetlitve na vozliscih, zato osvetlitev nikakor ne more biti mocnejsa znotraj mnogokotnika. Ko v praksi uporabljamo Gouraud-ovo metodo sencenja moramo poskrbeti, da povrsino, ki jo sencimo dovolj na drobno razdelimo na mnogokotnike (navadno trikotnike in kvadrate), drugace sencen model nikakor ni kakovosten.

Slika 13
Ker je izvor svetlobe tocno nad desnim ogljiscem je to ogljisce popolnoma svetlo (vozliscna normala in linija do izvora svetlobe sta vzporedna...).
[1] Fundamentals of Three-Dimensional Computer Graphics, Alan Watt, Addison-Wesley 1989
[2] C++ Primer Plus, Stephen Prata, Waite Group Press 1998, Corte Madera, CA