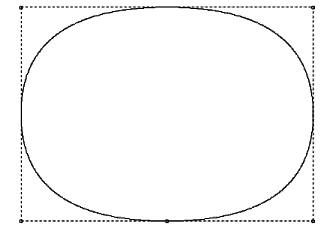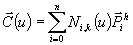
The goal of this seminar is to write a software for NURBS (Non-Uniform Rational B-Spline). The software should compute the curves and display the results in graphics. The curve is fixed with the number of control points and the degree of curve. NURBS has two significant propeties. The first property - non-localness - implies that, althought a control point heavily influences that part of the curve most close to it, it also have some effect on all the other curve. The second property of NURBS is that the curve passes only trough the first and the last control point. Each control point has beside the x and y coordinates also definite weight w. Greather the weight is, more close to the control point the curve will pass and contrary.
Namen seminarske naloge je napisati program, ki bo izrisal krivuljo NURBS. Krivulja je določena s kontrolnim poligonom, ki ga sestavljajo kontrolne točke. Te kontrolne točke imajo poleg koordinat x in y v ravnini tudi tretjo komponento, utež w. Uteži imajo bistven vpliv na sam potek krivulje. Večja kot je utež določene točke, bolj se krivulja približa kontrolni točki, ter manjša kot je utež, bolj se krivulja oddaljuje od kontrolne točke. Krivulja pri tem poteka samo skozi prvo in zadnjo točko kontrolnega poligona, ostalim kontrolnim točkam pa se le pribliza.
NURBS (Non-Uniform Rational B-spline) krivulje in ploskve se pogosto uporabljajo v računalniški grafiki, ker lahko z njimi dosežemo lepo ukrivljene in gladke krivulje oz. ravnine. Krivulje so definirane s poligonom kontrolnih točk in utežnostnimi faktorji. Njihovi značilnosti pa sta predvsem ta, da povečana utež posamezne kontrolne točke ne vpliva samo na tisti del krivulje, ki se nahaja v bližini te točke, ampak vpliva na celotno krivuljo. To pomeni, da vsaka točka kontrolnega poligona prispeva k oblikovanju celotne krivulje. Druga značilnost pa je ta, da krivulja poteka samo skozi prvo in zadnjo točko kontrolnega poligona, vmesnim točkam pa se samo približa oz. se od njih oddalji, odvisno pač od velikosti utežnostnega faktorja.
Kot že ime pove, so krivulje sestavljene iz t.i. B-zlepkov. Ti B-zlepki pa niso nič drugega kot kubični polinomi. Krivulja je definirana kot zaporedje točk, ki jih dobimo s pomočjo naslednje enačbe:
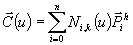
Pri tem je potrebno povedati, kaj posamezne oznake predstavljajo:
Značilnost homogenih koordinat je v tem, da so način zapisa n+1 dimenzionalnega Evklidovega prostora v n-dimenzionalen projekcijski prostor. Tako imamo v homogenih koordinatah poleg treh koordinat x,y še četrti zapis, ki pa v našem primeru predstavlja utežnostni faktor w. Tako ima naš vektor kontrolnih točk naslednjo obliko:
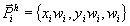
Pri tem nam indeks i pove, za katero kontrolno točko poligona gre, indeks h pa, da gre za homogen zapis vektorja. Iz vektorja kontrolnih točk lahko vidimo, da so posamezne koordinate že pomnožene v utežnostnim faktorjem w. Vedeti moramo, da so točke, ki jih dobimo iz Enačbe 1, zapisane prav tako v homogenih koordinatah. Vzdolž krivulje se vrednost utežnostnega faktorja iz točke v točko spreminja. S tem dobljenim faktorjem je potrebno deliti komponente vektorja C.
Definirati je potrebno tudi normirano funkcijo B-zlepka Ni,k. Ta je določena s pomočjo Cox-de-Boor-ove rekurzivne enačbe in se glasi:

Ker pa so krivulje višjega reda (k>1), dobimo ostale vrednosti za B-zlepke z naslednjo enačbo:
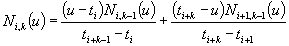
Kot lahko iz indeksov razberemo, gre res za rekurzivno formulo. Za izračun Ni,k potrebujemo tako Ni,k-1 kot Ni+1,k-1. Pri tem je:
Potrebno je povedati, da imamo v primeru n=6 7 kontrolnih točk; torej n+1 kontrolnih točk. Določiti moramo še vrednosti za vozliščne vektorje. Pri tem si pomagamo z naslednjimi pogoji:

Drugače pa lahko vozliščni vektor zapišemo tudi v naslednji obliki:
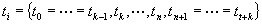
Iz Enačbe 6 lahko torej vidimo, da se v začetni in končni točki vrednost ponovi k-krat. Poleg tega moramo pri izračunu normiranih funkcij B-zlepkov upoštevati tudi naslednje kriterije:
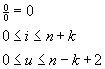
Program, ki bo podrobneje obrazložen v naslednjem poglavju, temelji na enačbah, ki so bile predstavljene zgoraj. V grobem pa se bo delil na dva dela. Prvi je računski del, v katerem se izračunavajo vrednosti, drugi del pa je grafični, ki služi za prikaz rezultatov s pomočjo grafa.
Vrnitev na kazaloProgram je napisan s programskim jezikom FORTRAN90. Zanj sem se odločil predvsem zaradi predhodnega znanja s tem jezikom. Poleg tega pa ta program, ki deluje v okolju WINDOWS 95 podpira tudi grafiko.
Program se prične z branje vhodnih podatkov. Le ti se namreč preberejo iz datoteke z imenom Polje tock.DAT. Struktura datoteke pa je sledeča:
n k gostota
x(0) y(0) w(0) x(1) y(1) w(1) .... x(n) y(n) w(n)
Prvi trije podatki, ki jih program prebere iz datoteke so število kontrolnih točk, red krivulje ter gostota, ki nam predstavlja število intervalov krivulje. Naslednji del programa je namenjen predvsem pripravi za grafični prikaz rezultatov. Program namreč iz prebranih kontrolnih točk izračuna njihovo srednjo vrednost tako v x kot v y smeri. S tem dobimo težišče poligona kontrolnih točk. To težišče bomo potrebovali, da ga bomo postavili v središče zaslona.
Dx=max_x-min_x Dy=max_y-min_y x_init=suma_x/(n+1) tu se izračuna srednja vrednost v x smeri y_init=suma_y/(n+1) tu se izračuna srednja vrednost v y smeri x_delitev=INT(780.0/Dx/1.) y_delitev=INT(580.0/Dy/1.)
Zopet sledi nekaj ukazov, s katerimi se določi barva in izriše zunanji okvir. Sledi izrisovanje poligona kontrolnih točk s črtkano zeleno crto, poleg tega pa se okoli kontrolnih točk izrišejo tudi rumeni krogci, ki prikazujejo kontrolne točke.
Za tem delom se prične matematični del programa. Na začetku imamo nastavljenih nekaj spominskih spremenljivk. Sledi določanje vrednosti vozliščnemu vektorju. Za tem se nahaja zanka, v kateri se izračunajo vrednosti in se končno tudi izrišejo. Število ciklov zanke je odvisno od parametra za dosego kontrolnih točk u ter od gostote oz. števila intervalov, ki smo so podani v datoteki. Naslednji del je tisti, ki predstavlja neposredno Cox-de-Boor- ovo rekurzivno enačbo. Pri tem je potrebno paziti, da imenovalec nima vrednosti nič. To se v programu tudi preverja. V tem delu se izračunajo vse potrebne vrednosti zlepkov, ki jih bomo potrebovali, če bomo hoteli izračunati vrednost nekega zlepka. Npr., če želimo izračunati vrednost N5,4(u), potem potrebujemo naslednja dva zlepka, ki sta za eno stopnjo manjša; to sta N5,3(u) ter N6,3(u). Ta dva zlepka pa sta zopet sestavljena iz po dveh zlepkov nižje stopnje. Ta del programa pa torej izračuna vrednosti za vse potrebne zlepke, če želimo določiti vrednost NURBS krivulje pri določeni vrednosti parametra u in stopnji krivulje k. Sledi sumiranje vrednosti, ki je v prvem poglavju podano z Enacbo 1.
do j=0,n
do h=0,k-1
if ((korak.GE.t(j+h)) .and. (korak.LT.t(j+h+1))) then
B(j+h,1)=1
else
B(j+h,1)=0
endif
enddo
do ii=2,k
do h=0,k-2
if ((t(j+h+ii-1)-t(j+h)).EQ.0) then
if ((t(j+h+ii)-t(j+h+1)).EQ.0) then
B(j+h,ii)=0
else
B(j+h,ii)=(t(j+ii+h)-korak)*B(j+1+h,ii-1)/(t(j+h+ii)-t(j+1+h))
endif
else
if ((t(j+h+ii)-t(j+h+1)).EQ.0) then
B(j+h,ii)=(korak-t(j+h))*B(j+h,ii-1)/(t(j+ii+h-1)-t(j+h))
else
B(j+h,ii)=(korak-t(j+h))*B(j+h,ii-1)/(t(j+ii+h-1)-
t(j+h))+(t(j+ii+h)-korak)*B(j+1+h,ii-1)/(t(j+ii+h)-t(j+1+h))
endif
endif
enddo
enddo
Cx=Cx+B(j,k)*x(j)*w(j)
Cy=Cy+B(j,k)*y(j)*w(j)
Cw=Cw+B(j,k)*w(j)
enddo
Ta del kode je tisti, ki torej predstavlja Cox-de-Boor-vo rekurzivno formulo. Za tem sledi izris premice med prejšnjo točko krivulje in sedaj izračunano točko krivulje. Vse skupaj se ponavlja dokler ne doseže program zadnje kontrolne točke.
Vrnitev na kazaloPri izdelavi programa za izris NURBS krivulj sem najprej pričel z matematičnim delom programa. Po tem, ko sem razčistil glede indeksov, vozliščnih vektorjev in parametra u, sem pričel z nastavljanjem Cox-de-Boor-ove rekurzivne enačbe. Vse skupaj je nekako delovalo, vendar sem kot rezultat vedno dobil le premice in nobenih krivulj. V literaturi sem namreč zasledil, da v primeru, ko je stopnja k=2, govorimo o krivuljah. V primeru ko je k=2 lahko, če pogledamo Enačbo 3 in Enačbo 4 ugotovimo, da se v Enačbi 4 na določenem odseku spreminja samo parameter u, vse ostalo pa so konstante. Rezultat tega je, da če se parameter u spreminja linearno, potem se linearno spreminja tudi vrednost normirane funkcije B-zlepka. Da je vse skupaj res, se lahko prepričamo tudi s programom, če mu za stopnjo krivulje na začetku podamo vrednost 2. Krivulja bo v tem primeru potekala po daljicah, ki povezujejo točke kontrolnega poligona. Na koncu se je izkazalo, da je stopnja lahko tudi vecja od 2 in šele v tem primeru dobimo neke gladke krivuljo po poligonu kontrolnih točk. Poleg teh se mi je pojavil tudi problem, ko je bil utežnostni faktor pri dolocenem u-ju enak nic in je program je javljal napako. Do te napake je prihajalo, ko se je krivulja povsem približala končni točki. Napako sem odpravil s tem da se vedno preveri vrednost utežnostnega faktorja.
Drugi problem pa se je pojavil po tistem, ko je bil matematični del programa napisan, dodati pa je bilo potrebno še grafični prikaz rezultatov. V dobri veri, da ne bom imel težav pri prenosu izvorne kode, ki sem jo pisal v FORTRANU90, na G77, sem pričel z vključevanjem ukazov za grafiko iz knjiznice PHIGS v izvorno kodo. Ko sem vse skupaj poskušal prevesti, pa je prevajalnik javil kup napak. V mojem programu se namreč nahajajo tudi zapisi, ki pa sem jih pricel številčiti z nič, ker so bili takšni indeksi tudi v literaturi. FORTRAN90 je vse skupaj brez problemov prevedel. Ko pa sem to poskušal s FORTRAN77 je javil napako. Tako sem se odločil, da bom tudi grafiko napisal v FORTRANU90, saj jo le ta tudi podpira.
Glede izboljšave programa sem imel v mislih predvsem to, da bi imel vgrajeno možnost sprotnega spreminjanja položaja kontrolnih točk ter njihovih utežnostnih vrednosti. S tem ko bi miško pozicionirali na eno od točk kontrolnega poligona in pritisnili na gumb, bi lahko to točko prestavili na neko drugo poljubno mesto. Po prestavitvi te točke, pa bi se nam krivulja zopet na novo izrisala. Na podoben način bi bil narejen tudi del za spreminjanje utežnostnih faktorjev točk.
Vrnitev na kazaloV tem delu je prikazanih nekaj rešitev primerov, ki jih je dal program. Pri tem bomo lahko videli, kako se krivulja spreminja, če spreminjamo položaj posameznih kontrolnih točk, kot tudi če spreminjamo velikost utežnostnega faktorja posamezne točke.
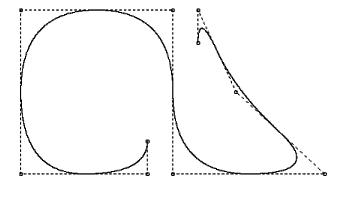
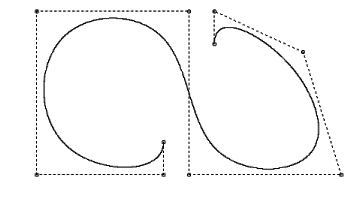
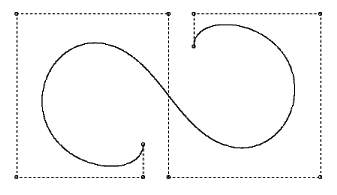
Na zgornjih slikah lahko vidimo, kakšen vpliv ima sprememba posamezne kontrolne točke poligona na celotno krivuljo. Poleg tega lahko tudi vidimo, da se oblika krivulje spreminja tudi v odvisnosti od stopnje krivulje k. Za primer k=3 je značilno, da se krivulja dotika vsake daljice med posameznimi točkami kontrolnega poligona. Ta pojav pa izgine, ko je k>3. Na naslednjih primerih bomo lahko videli, kako utežnostni faktor vpliva na obliko krivulje.
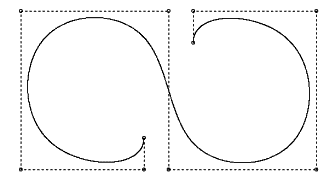
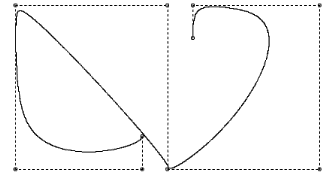
Eden izmed prikazanih primerov je tudi izrisana oblika elipse, ki jo dosežemo pri k=3.