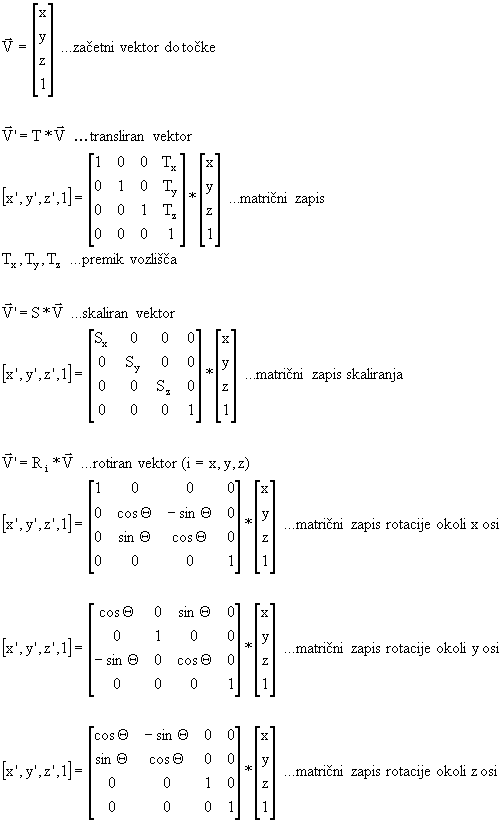1. ABSTRACT

2. DEFINICIJA NALOGE

3. OSNOVNI PRINCIPI PRIKAZA 3D OBJEKTOV

4. ALGORITEM MARCHING CUBE

4.1 Prikaz objekta z uporabo voxlov
4.2 Algoritem Marching Cube

4.2.1 Osnovna ideja
4.2.2 Prikaz algoritma v 2D
4.2.3 Prikaz algoritma v 3D
4.2.4 Izboljšanje algoritma

5. PROGRAMSKA KODA IN OPIS

5.1 Diagram poteka za algoritem Marching Cube
5.2 Transformacije v 3D prostoru

6. ZAKLJUČEK

7. LITERATURA

The Marching Cube algorithm is used in volume rendering to reconstruct an isosurface from a 3D field of values. The basic principle is subdevide space into a series of small cubes. The algorithm then instructs us to "march" through each of cubes testing the corner points and replacing the cube with an appropriate set of triangles. The result is a smooth surface that approximates the isosurface.

V programskem jeziku JavaScript z emulacijo knjižnice PHIGS izdelajte program, ki predstavi algoritem Marching Cube. To je algoritem za rekonstrukcijo 3D površin iz 3D podatkovne baze. Program naj z izbiro ustreznih oglišč prikaže vseh petnajst variant voxlov, ki jih algoritem namešča na ustrezno mesto.

Za prikaz 3D objektov se v programskih kodah uporabljajo algoritmi, ki temeljijo na štirih najpogostejših oblikah prikaza:
1. poligonski-površina objekta je mrežena s poligonskimi površinami,
2. bikubični parametrični površinski zlepki ali B-spline površine,
3. geometrija trdnih teles-Constructive Solid Geometry (CSG) prikaže objekt sestavljen iz primitivov,
4. tehnike deljenja površine-vključujejo objekt v prostor z datoteko točk površine.

4.1 Prikaz objekta z uporabo voxlov

CSG podatkovna baza ne opredeljuje notranjost ali zunanjost in meje objekta. Obstajajo pa tri tehnike, ki to opredeljujejo:
1. CSG sledenje žarkov,
2. dopolnitev podatkovne baze za prikaz pixla s prostorsko koordinato-voxel,
3. uporaba algoritma Z-buffer.

Voxli so primerni za volumski prikaz objektov, ki nimajo ostrih geometrijskih robov:
- v medicini, kjer pridobimo bazo podatkov z računalniško tomografijo (CT) in magnetno resonanco (MR),
- v tehniki za vizualizacijo termičnih in tokovnih polj,
- v geologiji za prikaz volumskih geoloških sestavov.
Osnovni podatki, ki opišejo voxel so:
- položaj X=(x, y, z)
- barva C(X)
- prosojnost A(X)
Mreženje volumna z voxli zahteva za ustrezen prikaz površine:
- ustrezno gosto mrežo,
- aproksimacijo med vozlišči voxlov za ustrezno gladkost površine.
Za mreženje z voxli potrebujemo za realno gladkost in istovetnost modela s podatki ustrezno datoteko podatkov. 3D podatkovno bazo objekta pridobimo iz sekvenc objekta pridobljenih s presevanjem gama žarkov skozi objekt.Velikost voxlov je lahko določena kar z odmikom med posameznimi rezinami.

4.2 Algoritem Marching Cube

Algoritem Marching Cube je namenjen za rekonstrukcijo površine iz 3D podatkovne baze objekta. To podatkovno bazo v medicini dobimo z računalniško tomografijo (CT) in magnetno resonanco (MR).

4.2.1 Osnovna ideja

3D območje prostorsko porazdelimo v mrežo kock-voxlov. Algoritem potuje skozi posamezne kocke in preverja ali so voxli znotraj, zunaj ali pa sekajo rob površine. Glede na oceno znotraj-1, zunaj-0 in na robu namesti voxel z ustreznim zbirom trikotnikov, ki najnatančneje opisuje geometrijo v tem predelu površine.

4.2.2 Marching Cube v ravnini

Na spodnjih slikah je predstavljena osnovna zamisel gradnikov, ki sestavljajo mrežo ravninskega lika in poljuben lik, ko mu na sosednji sliki mrežo razdelimo na polovico. Z razpolovitvijo mreže že pridobimo dovolj gladek opis robu 2D lika.



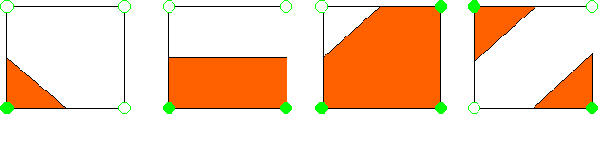
Slika1. Variante kvadratov za predstavitev algoritma v ravnini



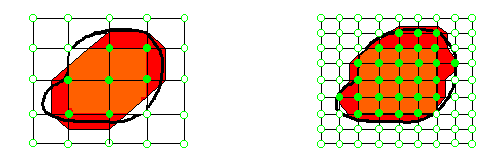
Slika 2. Mreženje v ravnini in podvojitev gostote mreže za predstavitev algoritma v ravnini

4.2.3 Marching Cube v 3D prostoru

V 3D prostoru tvorimo podatkovno bazo iz podatkov pridobljenih z delitvijo objekta na rezine. Voxel, ki ga vpeljemo za rekonstrukcijo 3D površine ima 8 oglišč in s tem 2⁸ = 256 možnih kombinacij ali je oglišče znotraj ali zunaj telesa. Z geometrijskimi transformacijami zmanjšamo število variant voxlov na vsega 15, ki jih pokaže spodnja slika.



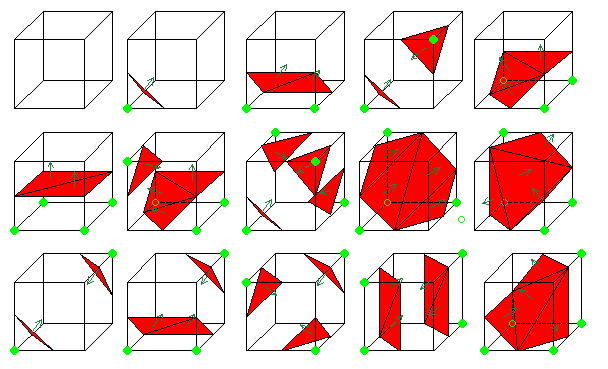
Slika 3. Petnajst kombinacij voxlov
Algoritem s "korakanjem" skozi vsak voxel preizkuša, ali so oglišča znotraj, zunaj ali na robu površine. Glede na določitev statusa voxla in števila oglišč znotraj ali zunaj površine algoritem določi, katera kocka spada na določeno mesto.
Natančneje pa voxli oblikujejo 3D površino po zaporedju:
1. branje podatkovne baze za štiri rezine,
2. določitev položaja voxla glede na štiri točke na eni in štiri točke na drugi rezini,
3. oštevilčenje oglišč voxla,
4. branje oštevilčenja robov glede na oglišča,
5. iskanje sečišča površine in robu voxla z interpolacijo,
6. izračun normal za voxel in poligonske trikotnike,
7. izhod oglišč in normal trikotnikov.

4.2.4 Izboljšanje algoritma

Prvotni algoritem Marching Cube je izboljšan glede hitrosti rekonstrukcije površine in njene gladkosti.

Preračunan položaj oglišč voxla in trikotnikov shranimo še za vse sosednje, tako da z interpolacijskimi popravki zadostimo podatkovni bazi objekta. Hitrost rekonstrukcije povečamo tudi z zmanjšanjem resolucije in povprečenjem vrednosti baze podatkov. S tem izgubimo nekaj detajlov na prikazu objekta, vendar pa hitrost rekonstrukcije še posebno pri rotaciji objekta bistveno povečamo.
Za boljšo gladkost površine pa premaknemo oglišča voxlov po robu do primerne površinske točke glede na sosednje voxle. Tako nadgradnjo algoritma imenujemo "adaptivne korakajoče kocke".

5.1 Diagram poteka za algoritem Marching Cube

Prikaz kocke Marching Cube lahko izvedemo na več načinov:
1. Narišemo žični model kocke in za izris poligonov uporabimo podatkovno bazo vozlišč trikotnikov. Podatkovno bazo beremo kot je organizirana. To metodo smo v programski kodi uporabili.
2. Uporabimo enak postopek kot zgoraj, le da beremo podatkovno bazo kar z IF stavki.
3. Narišemo žični model kocke in poligonsko kombinacijo v "osnovnem položaju". To kombinacijo pa na dejansko izbrana vozlišča zarotiramo v pravilni položaj.
4. Posamezne kombinacije ločimo po lastnostih glede na položaj kliknjenih vozlišč ( na istem robu, na ploskovni diagonali, na diagonali telesa, ... ). Za izris trikotnikov uporabimo preurejeno podatkovno bazo trikotnikov.
Izbran je zapis programske kode v jeziku Java Script z vključitvijo Javine knjižnice PHIGS. Ustrezno poligonsko kombinacijo smo dobili iz podatkovne baze trikotnikov, kar je razvidno iz diagrama poteka.


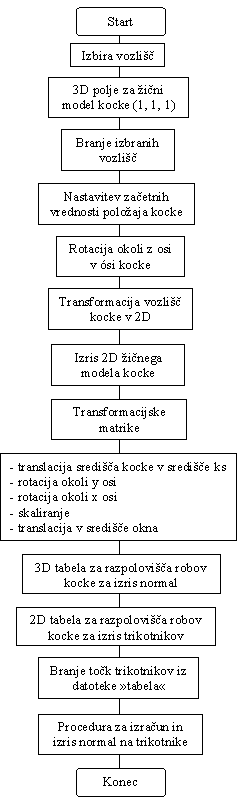
Slika 4. Diagram poteka naše programske kode

5.2 Transformacije v 3D prostoru

Transformacije v 3D prostoru izvajamo v lokalnem koordinatnem sistemu v homogenih koordinatah x, y, z. Transformiranim točkam nato odvzamemo koordinato z in jih zapišemo v globalni koordinatni sistem X, Y, ki je seveda zaslon računalnika. Osnovne transformacije v prostoru so:
- translacija,
- skaliranje,
- rotacija.

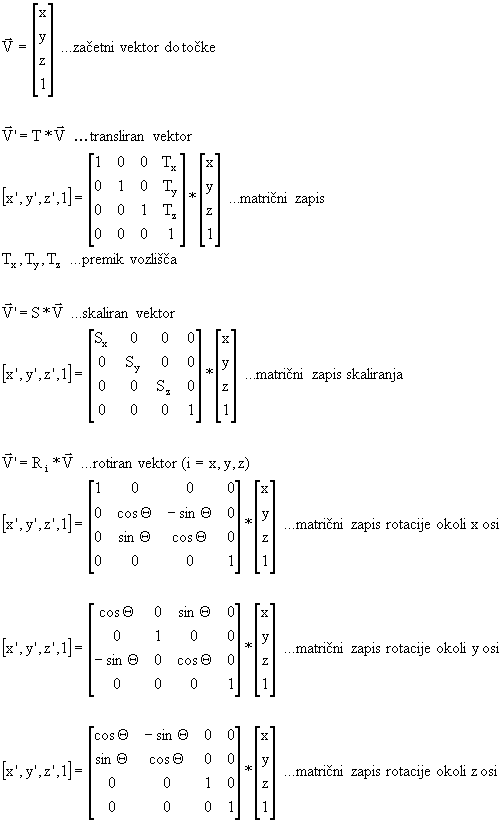
Slika 5. Transformacijske matrike v 3D prostoru

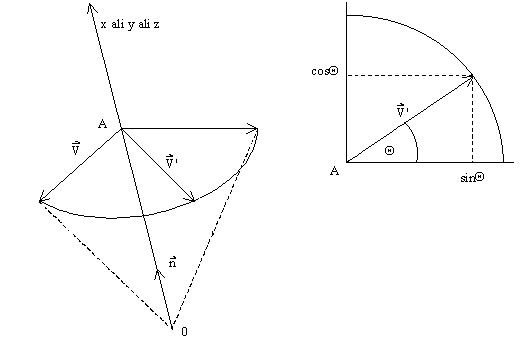
Slika 6. Rotacija okoli x, y ali z osi

Program je zapisan v jeziku Java Script, ki skupaj s knji�nico PHIGS nudi zadostno podporo za tovrstni prikaz objektov. Za razmnožitev kock v 3D prostor in aplikacijo algoritma Marching Cube na mejah objekta pa je ta jezik neprimeren. Saj hočemo prav s tem algoritmom preseči omejitve hitrosti prikaza, ki jo dovoljuje programska in strojna oprema. Torej noben programski jezik in procedura ni zadosti "hitra". Za konkretno aplikacijo je programska koda za algoritem Marching Cube zapisana v jeziku C.

[1] Peter Hribar; SPOZNAJMO JAVASCRIPT; Flamingo 1998
[2] Alan Watt; 3D COMPUTER GRAPHICS; Addison-Wesley 1994
[3] Lorensen W. E. and Cline H. E.; Marching Cubes: a high resolution 3D surface construction algorithm; Computer Graphics, 21 (4), 163-9;1987

• Kazalo

ZAGON PROGRAMA