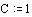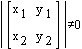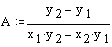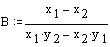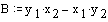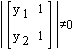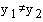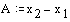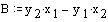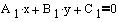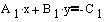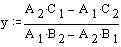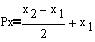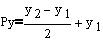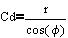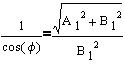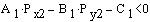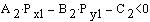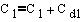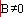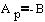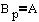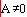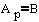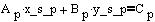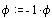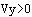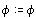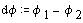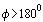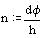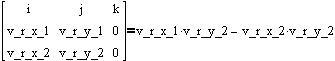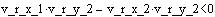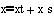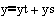Zaokrožitev daljic s krožnim lokom
Boštjan Zupanc
24.januar,1999
Abstract:
This program rounds up two different straith lines into an arc with precalculated radius "r".It also calculates a crossing of this two lines and start and end of the arc.
Presek dveh črt je potrebno zaokrožiti s krožnim lokom. Program v JS in Phigs naj za poljubni dve daljici najde presek in izračuna nova konca daljic, začetek in konec loka ter predstavi algoritem izračuna v podprogramu.
Vhodni podatki so točke daljic, velikost krožnega loka in delitveni kot.
Glede na točke daljic določimo osnovni enačbi premic.
S pomočjo dobljenih enačb premic izračunamo presečišče premic.
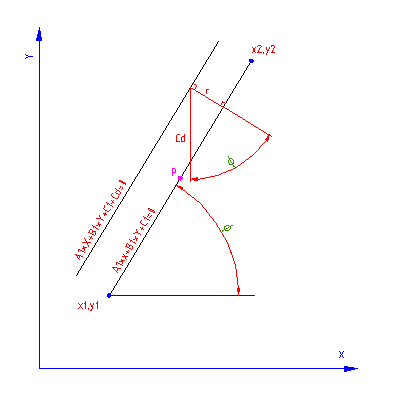
Središče krožnega loka izračunamo s pomočjo presečišča vzporednic, ki so od osnovnih premic oddaljeni za "r".Enačbo vzporednic določimo s izračunom vrednosti koeficijenta "Cd" ter določitvijo predznaka "Cd", glede na testno točko ,ki ga prištejemo osnovni enačbi premice. Lego vzporednic oziroma krožnega loka določimo s testnimi točkami "P1,P2".

Začetek in konec krožnega loka izračunamo tako, da na osnovne premice tvorimo pravokotnice, ki potekajo skozi središče krožnega loka. Presečišče osnovne premice in njene pravokotnice je začetek oziroma konec krožnega loka "Q1,Q2".

Skozi središče krožnega loka in začetek oziroma konec krožnega loka potegnemo vektor. Določimo kot vektorjev z x-osjo. Izračunamo razpon kota krožnega loka. Določimo smer krožnega loka in število delitev krožnega loka.Kot razpona razdelimo na podkote glede na vhodni podatek delitveni kot "h".

Ko imamo poznane podkote lahko izračunamo točke loka zaokrožitve.
Enačbo premice sem določil po splošni enačbi za premico. Ta oblika enačbe omogoča enostaven popis premic. Pri določitvi splošne enačbe premice imamo sistem dveh enačb, ki je enkrat nedoločen. Za rešitev takega sistema je potrebno za eno neznanko izbrati vrednost, ostale pa se izračunajo. Da ima tak sistem enačb rešitev mora veljati, da je determinanta matrike koeficientov različna od nič. če to ne velja moramo vrednost izbrati drugi oziroma tretji neznanki.
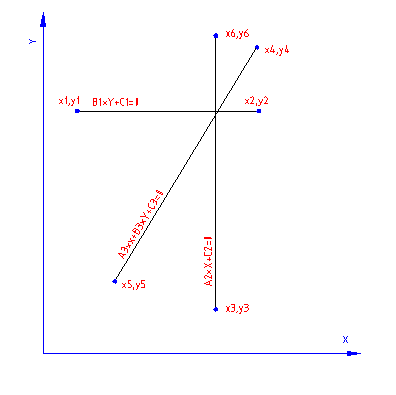
Sistem enačb za določitev enačbe premice, ki poteka skozi točko x1,y1 in točko x2,y2:


Prva možnost:
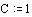
Pogoj, da je sistem rešljiv:
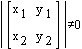

Rešitev:
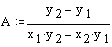
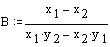
Druga možnost:

Pogoj, da je sistem rešljiv:

Rešitev sistema:
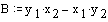

Tretja možnost:

Pogoj, da je sistem rešljiv:
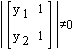
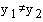
Rešitve
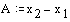
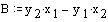
S pomočjo dobljenih enačb lahko izračunamo presečišče premic, ki ob pogoju, da premice niso vzporedne, vedno enolično določeno.
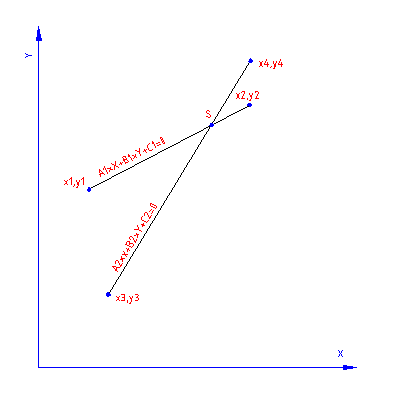
Sistem enačb:
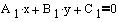

Homogen sistem enačb:
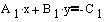

Pogoj za rešitev sistema enačb:


Rešitev sistema enačb:

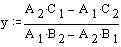
S tesntnimi točkami določimo, na kateri strani bo središče krožnega loka. Testnjo točko sem izbral po priporočilu literature[2] na sredini daljice. Tako dobimo nakateri strani glede na osnovno premico bo vzporednica ležala in sicer vzporednica glede na prvo premico bo med prvo premico in testno točko na drugi premici in obratno.
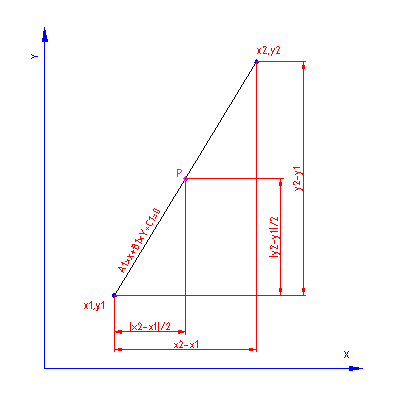
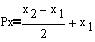
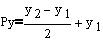
Vrednost koeficijent "Cd" nam določa , za koliko se mora povečati koeficijent premice C, da bo nova premica glede na osnovno vzporedna in oddaljena za določeno razdaljo. V našem primeru za razdaljo "r".
Absolutna vrednost je:
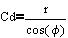
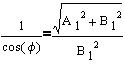
V primeru ko je B=0 velja naslednja zveza:


Pri določanju novih premic, ki so oddaljene za točno določeno razdaljo od osnovne premice dobimo dve možnosti, ali se premica dvigne ali spusti za to vrednost. To določimo spomočjo testnih točk.
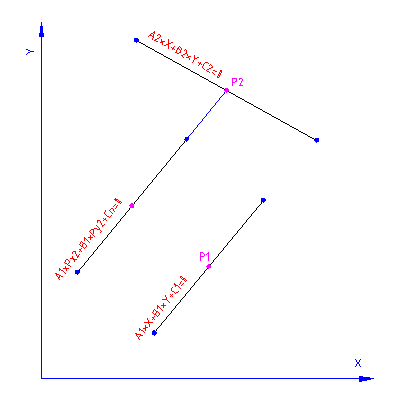
če je vrednost enačbe premice v testni točki negativna potem je tudi predznak "Cd" negativen, drugače pa je pozitiven.
Pogoj za prvo premico, da se spremeni koeficijetu "Cd1" predznak: Izračun vrednosti premice v testni točki druge premice.
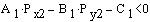
Pogoj za drugo premico, da se spremeni predznak koeficijentu "Cd2": Izračun vrednosti premice v testni točki prve premice.
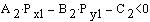

Enačbo vzporednice dolčimo tako, da koeficijentu "C" prištejemo "Cd" pri obeh enačbah premice.

Za prvo premico:
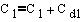
Za drogo premico:


Splošna enačba premice:

Pri pogoju da eden od koeficijentov "A" ali "B" je različen od nič, lahko enačbo pravokotnice skozi središče s koordinatami x_s_p, y_s_p določimo:
Primer ko je:
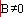
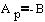
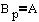
Ali ko je:
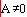
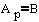

Predznak spremenimo pri koeficijentu, ki je različen od nič. Primera da sta oba koeficijenta nič ni pri premici. Po določitvi koeficijenta "A_p" in "B_p" izračunamo še koeficijet "C_p" pri dani točki.
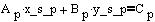
Skozi središče in začatek oziroma konec krožnega loka določimo vektorja.
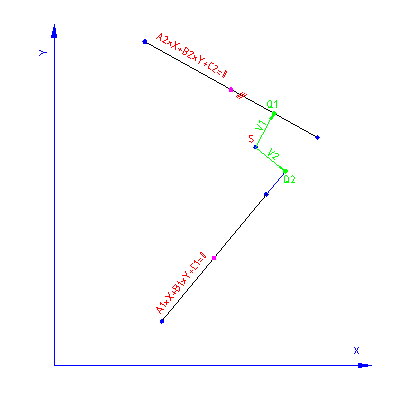
Kot izračunamo po enačbi, da je arc cosinus kota enak količniku projekcije vektorja na x-os z absolutno vrednostjo vekorja. Funckija arc cosinus zavzema dve vrednosti pri argumentu in sicer plus in minus izračunanga kota. Zato si pri določitvi kota pomagamo s projekcijo vektorja na y-os. če je projekcija vektorja na y-os usmerjena negativno je predznak kota negativen, drugače pa pozitiven.
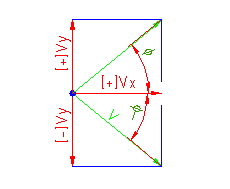
Izračun kota:

Določitev predznaka:
Projekcija vektorja na y-os je negativna:

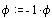
Projekcija vektorja na y-os je pozitivna:
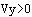
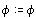
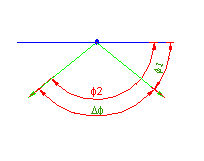
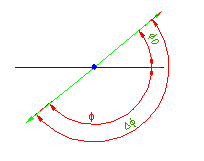
Razpon krožnega loka izračunamo kot razliko kotov med obema vektorjema.
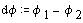
Maksimalen razpon kota krožnega loka je lahko 180 stopin.
če je izračunan razpon večji je dejanski kot izračunan po naslednji enačbi:
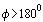

število delitev izračunamo glede na vhodni podatek "h", ki nam določa delitveni kot. Delitveni kot je kot, ki razdeli celotni kot na manjše kote.

Izračun števila delitev.
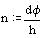
Smer poteka krožnega loka izračunamo s pomočjo vektorskega produkta. Pri vektorskem produktu dobimo nek novi vektor, ki je pravokoten na vektorja vektorskem produktu. Usmerjenost vektorja je določena z položajem obeh vektorjev. če je najmanjši kot od prvega vektorja v vektorskem produktu do drugega vektorja v vektorskem produktu negativen je usmerjenost vektorja negativna in obratno. Tako lahko določimo smer poteka krožnega loka od prvega vektorja v vektorskem produktu. Vektorski produkt:

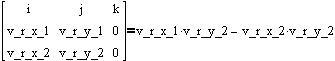
Vektor usmerjen v pozitivno. Smer krožnega loka je negativna.
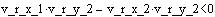
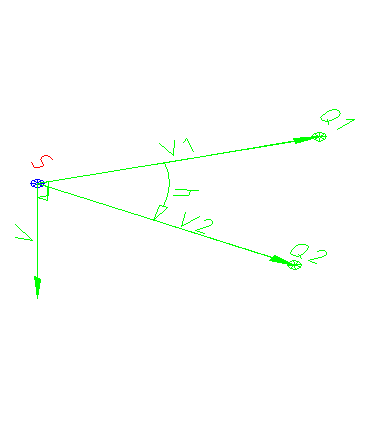
Vektor usmerjen v negativno. Smer krožnega loka je pozitivna.


Točke zaokrožitve loka določimo z izračunanimi podkoti. Dolžino krožnega loka "r" proiciramo na osi za vsak podkot.
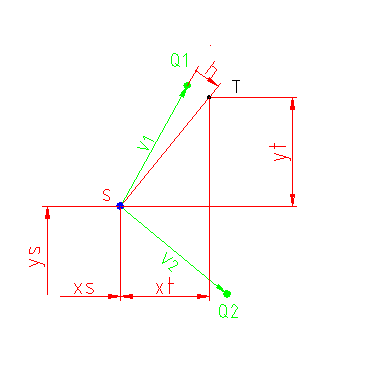
Točka zaokrožitve "T" s koordinatami "x" in "y".
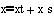
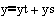
Program je napisan v JS z dodatno knjižnico Phigs , ki omogoča risanje na zaslon. Program ob vnosu točk daljic in velikosti krožnega loka zaokrožitve izračuna navidezno presečišče daljic, središče krožnega loka, začetek in konec krožnega loka, točke za risanje krožnega loka in izris grafike na zaslon. Okno izrisa ima meje od 0,0 do 10,10. Program se zažene ob vnosu podatkov in pritisnitvi gumba "Obnovi".
Pri določitvi enačbe premice imamo sistem z dvema enačbama in trem neznankam. Zato določimo eno neznanko ter ostali dve izračunamo. Določitev neznanke pa vpliva tudi na pogoj, da je sistem rešljiv. Zato se v programu izračunajo vse tri možne kombinacijein ena od kombinacij, da vedno enačbo premice. Program izračunava enačbe tako, da izračuna vse kombinacije in zadnja enačba premice, ki ostane v spominu se uporabi naprej v programu.
Prva možnost
for(i=1;i<=2;i++){
if(yt[2*i-1]*xt[2*i]!=yt[2*i]*xt[2*i-1]){
a1=yt[2*i-1]-yt[2*i];
b1=xt[2*i]-xt[2*i-1];
d1=xt[2*i-1]*yt[2*i]-xt[2*i]*yt[2*i-1];
a[i]=a1/d1;
b[i]=b1/d1;
c[i]=1; }
Druga možnost
if(xt[2*i-1]!=xt[2*i]){
a1=yt[2*i]-yt[2*i-1];
c1=yt[2*i-1]*xt[2*i]-xt[2*i-1]*yt[2*i];
d1=xt[2*i-1]-xt[2*i];
a[i]=a1/d1;
c[i]=c1/d1;
b[i]=1; }
Tretja možnost
if(yt[2*i-1]!=yt[2*i]){
b1=xt[2*i]-xt[2*i-1];
c1=yt[2*i]*xt[2*i-1]-xt[2*i]*yt[2*i-1];
d1=yt[2*i-1]-yt[2*i];
b[i]=b1/d1;
c[i]=c1/d1;
a[i]=1; }}
Pri računanju presečišča mora biti izpolnjen pogoj da, premici nista med sabo vzporedni.
y_s=(a[2]*c[1]-a[1]*c[2])/(a[1]*b[2]-a[2]*b[1]);
x_s=(c[2]*b[1]-c[1]*b[2])/(a[1]*b[2]-a[2]*b[1]);
Testno točko določimo na obeh daljicah na sredini daljice.
for(i=1;i<=2;i++){
px[i]=((xt[2*i]*1-xt[2*i-1]*1)/2)+xt[2*i-1]*1;
py[i]=((yt[2*i]*1-yt[2*i-1]*1)/2)+yt[2*i-1]*1; }
Vrednost "cd" določimo za obe premici tako, da ob prištetju te vrednosti k osnovni enačbi premice dobimo novo vzporedno premico, ki je oddaljena od osnovne za "r"(najkrajša oddaljenost).
for(i=1;i<=2;i++){
cd[i]=r*Math.sqrt(a[i]*a[i]+b[i]*b[i])/b[i]*b[i]; V primeru ko je b=0 se izračuna "cd" po naslednji enačbi.
if(b[i]==0)cd[i]=r/a[i];
Absolutna vrednost "cd".
if(cd[i]<0)cd[i]=-1*cd[i]; }
Predznak konstanti cd izračunam tako, da testiramo ali je vrednost enačbe prve premice v testni točki druge premice, in obratno, večja od nič ali manjša. če vrednost manjša od nič je preznak "cd1" negativen drugače pustimo pozitiven.
if(-a[1]*px[2]-b[1]*py[2]-c[1]<0){
cd[1]=cd[1]*(-1); }
Predznak "cd2" določimo analogno kot "cd1"
if(-a[2]*px[1]-b[2]*py[1]-c[2]<0){
cd[2]=cd[2]*(-1); }
Osnovno enačbo premice spremenimo v enačbo vzporednice tako da vrednost "cd" prištejemo "c".
for(i=1;i<=2;i++){
c[i]=c[i]+cd[i]; }
Presčišče izračunamo že znanem postopku.
y_s_p=(a[2]*c[1]-a[1]*c[2])/(a[1]*b[2]-a[2]*b[1]);
x_s_p=(c[2]*b[1]-c[1]*b[2])/(a[1]*b[2]-a[2]*b[1]);
Enačbo vzporednic spremenimo v osnovne enačbe.
c[1]=c[1]-cd[1];
c[2]=c[2]-cd[2];
Premica je pravokotna če medsabo zamenjamo vrednosti koeficijentoma enačbe "a" in "b" in enemu od koeficijetov različnim od nič spremenimo predznak.
for(i=1;i<=2;i++){
a_p[i]=b[i];
b_p[i]=a[i];
Sprememba predznaka na koeficijentu "a_p" ali "b_p" enačbe pravokotnice ob pogoju, da je koeficjent različen od nič.
if(b_p[i]!=0)b_p[i]=-1*b_p[i];
else a_p[i]=-1*a_p[i];
Izračun koeficijenta c_p.
Ko imamo določene koeficijente a_p in b_p lahko določimo še koeficijent cp, ki je odvisen od točke skozi katero poteka. V našem primeru potekata pravokotnici skozi srdišče krožnega loka.
c_p[i]=-a_p[i]*x_s_p-b_p[i]*y_s_p;
Začetek in konec krožnega loka izračunamo kot presečišče pravokotnice in osnovne enačbe premice.
y_r[i]=(a_p[i]*c[i]-a[i]*c_p[i])/(a[i]*b_p[i]-a_p[i]*b[i]);
x_r[i]=(c_p[i]*b[i]-c[i]*b_p[i])/(a[i]*b_p[i]-a_p[i]*b[i]); }
Vektorje določimo zato, da si z njimi pomagamo pri določitvi smeri poteka krožnega loka.
v_r_x_1=x_r[1]-x_s_p;
v_r_y_1=y_r[1]-y_s_p;
v_r_x_2=x_r[2]-x_s_p;
v_r_y_2=y_r[2]-y_s_p;
Izračun kota drugega vektorja
fi_test=Math.acos(v_r_x_2/r);
Ugotavljanje pravilnega predznaka kota vektorja.
Ker funkcija arkus cosinus zavzema le pozitivne vrednosti kota si s pomočjo usmerjenosti projekcije vektorja na y-os pomagamo pri določitvi predznaka. če je projekcija vektorja usmerjena negativno je preznak izračuanega kota negativen drugače pa pozitiven.
if((v_r_y_2)<0){
fi_test=fi_test*(-1);
}
Izračun kota prvega vektorja
fi[0]=Math.acos(v_r_x_1/r);
Določitev pravilnega predznaka kota prvega vektorja
if((v_r_y_1)<0){
fi[0]=fi[0]*(-1); }
Absolutna vrednost razpona kota izračunamo kot razliko kotov prvega in drugega vektorja.
d_fi=Math.abs(fi[0]-fi_test);
Razpon kota ne more biti večji od 180 stopin. če je izračunana absolutna vrednost večja od 180 je dejanska vrednost kota razlika med polnim kotom(360 stopin) in izračunanim kotom.
if(d_fi>Math.PI){
d_fi=2*Math.PI-d_fi; }
število delitev izračunamo glede na vhodni podatek "h", ki nam določa delitveni kot. Delitveni kot je kot, ki razdeli celotni kot na manjše kote.
n=d_fi/h;
Smer poteka krožnega loka izračunamo s pomočjo vektorskega produkta. Pri vektorskem produktu dobimo nek novi vektor, ki je pravokoten na vektorja vektorskem produktu. Usmerjenost vektorja je določena z položajem obeh vektorjev. če je najmanjši kot od prvega vektorja v vektorskem produktu do drugega vektorja v vektorskem produktu negativen je usmerjenost vektorja negativna in obratno. Tako lahko določimo smer poteka krožnega loka od prvegavektorja v vektorkem produktu.
if((v_r_x_1*v_r_y_2-v_r_x_2*v_r_y_1)<0){
Delinemu kotu določimo predznak.
h=(-1*h); }
Umesne kote določimo tako da kotu prvega vektorja v vektorskem produktu prištevamo (n-1,število delitev minus 1 delitev ) delitvenih kotv.
for( i=1;i<=n;i++){
fi[i]=fi[0]+i*h; }
Ker ni število delitev vedno celo število vzamemo za končni kot, kot drugega vektorja v vektorskem produktu.
fi[i]=fi_test;
Radij je sestavljen iz množice točk, ki jih povežemo s črtami. Točke izračunamo ob izračunanih vmesnih kotih krožnega loka in projekcije polmera krožnega loka na x-os in y-os.
for(kk=0;kk<=i;kk++){
x[kk]=Math.cos(fi[kk])*r+x_s_p;
y[kk]=Math.sin(fi[kk])*r+y_s_p; }
Literatura
- 1
- Bronštejn and Semendajajev.
Matetamtični priročnik.
Tehniška založba Slovenije, 1997.
-
2
- Robert D.Miller.
InGraphics gems III. Academic press, 1992
Tehniška založba Slovenije, 1997.
Boštjan Zupanc
1999-2-22