1.0 Abstract
2.0 Uvod
3.0 Navodila
4.0 Teoretične osnove
4.1 Transfromacije
4.1.1 Rotacija točke v 3D prostoru
4.1.2 Skaliranje točke v 3D prostoru
4.2 Zapis transformacij v homogenih koordinatah
5.0 Zgradba programa
5.1 Izracun premera gredi in zatica
5.2 Prednastavitev vrednosti faktorjev transformacij - inicializacija
5.3 Zagon grafike
5.4 Funkcije, ki dolocajo zaporedje podprogramov
5.5 Izris slike, lokalnega in globalnega koodinatnega sistema
5.6 Izris vilic, bata in zatica
5.7 Skaliranje
5.8 Translacija
5.9 Rotacija
5.10 Kontrola tock znotraj obmocja slike
5.11 Resetiranje oz. postavitve slike v zacetni polozaj
6.0 Zagon programa
7.0 Zakljucek
1.0 Abstract
In the first part of the seminar there is represented a simple calculation of
piston, fork and straight pin for strain force.
Second part of the seminar is a graphical
representation of 3D-calculated part with the support of grapichal library
PHIGS. Some basic geometrical transforamtions are allowed, such as rotation,
scaling and translation.
2.0 Uvod
Namen izdelave programa za izris in preracun valjastega zatica po DIN 7 je spoznavanje teoretičnih osnov glede 3D transformacij ter spoznavanje programskega jezika HTML, Javascript in graficne knjiznice PHIGS.
3.0 Navodila
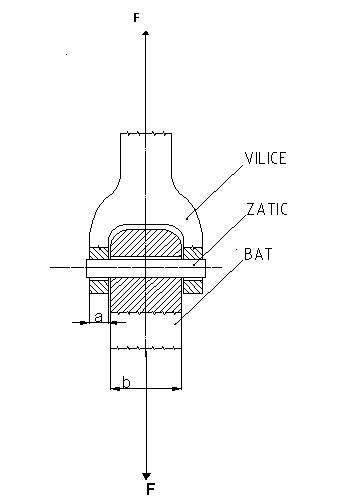
Izdelajte racunalniski program za kontrolo valjastega zatica (DIN 7), ki je obremenjen z natezno silo (glej sliko). Vhodni podatki so obremenitvena sila, material vilic, bata in zatica. Klasicne tabele oblikujte kot datoteke. Upostevajte staticne in dinamicne obremenitve.
Graficni del programa naj prikazuje 3D zicni model sklopa na sliki. Funkcionalni deli naj bodo razlicnih barv. Omogoci naj tudi tri osnovne geometrijske transformacije: rotacijo, translacijo in skaliranje. Vnos transformacijskih parametrov naj bo izveden preko enostavnega menuja. Objekt transformiranja naj bo sklop z zaticem brez kot in kotirnih crt.
4.0 Teoreticne osnove
4.1 Transformacije
4.1.1 Rotacija točke v 3D prostoru
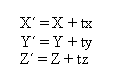
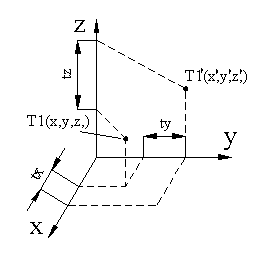
Običajno se rotacija izvaja okrog določene osi. Spodaj predstavljena rotacija
je okrog Z-osi. Princip za ostali dve transformaciji je isti le transformacijski
matriki se razlikujeta predstavljeni sta v točki zapis transformacij v homogenih
koordinatah (rotacija).
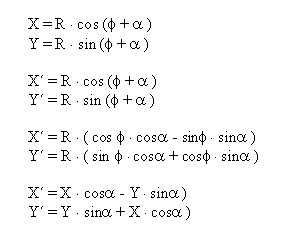
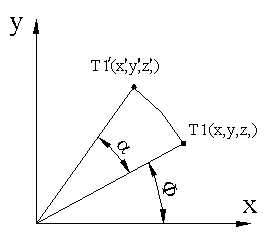
4.1.2 Skaliranje točke v 3D prostoru
-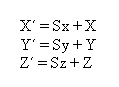
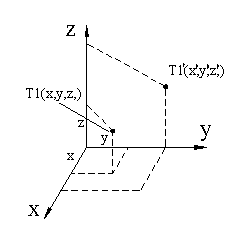
4.2 Zapis transformacij v homogenih koordinatah
4.2.1 Skaliranje
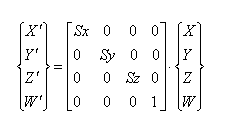
4.2.2 Translacija
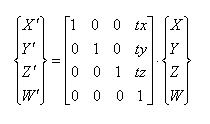
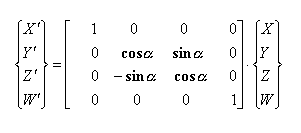
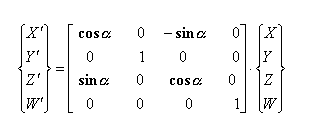
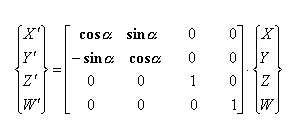
5.0 Zgradba programa
Program je zgrajen naslednje:
- Izracun
premera zatica
- Izracun sirine vilic
-Kontrola zatica na upogibno napetost
- Izracun sirine bata
- Izracun dolzine zatica
-
Prednastavitev vrednosti faktorjev transformacij - inicializacija
-
Zagon grafike
- Funkcije, ki dolocajo zaporedje podprogramov
]
- Izris slike, lokalnega in globalnega koodinatnega
sistema
- Izris valjev
- Izris zatica
- Skaliranje
- Translacija
- Rotacije
- Kontrola tock
znotraj obmocja slike
- Resetiranje oz. postavitve slike v
zacetni polozaj
- Izpis izracuna in vhodnih podatkov v novo okno
v urejeni obliki
5.1 Izracun premera zatica, sirine vilic in bata
Izracun premera zatica je izveden po spodnji enacbi. Zatic je obremenjen na strig.
Izracunani premer zatica se zaokrozi na prvi standardni premer zatica.
Sledi izracun sirine vilic po spodnji enacbi:

Pri racunanju sirine vilic in bata sem podal kriterij v obliki if stavka, ki nam prepoveduje uporabo materiala,
ki ima za manj kot 2 × slabso dopustno tlacno napetost.
Kontroliramo tudi upogibno napetost zatica in sicer po naslednji enacbi:

Izracun sirine zatica izracunamo po naslednji enacbi:
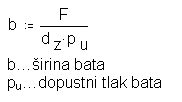
Toda izracun sirine bata samo glede na dopustno tlacno napetost zatica je premalo zato
bat kontroliramo se na natezno trdnost. Spodaj je vidna izpeljava izracuna.
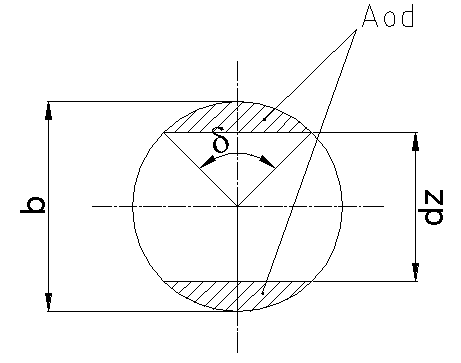
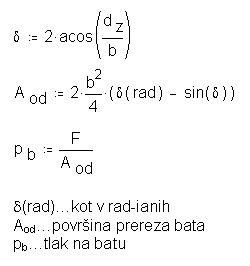
Ce bat ne prenese te natezne napetosti povecamo sirino bata
in sicer s pomocjo for zanke, ki nam poisce dovolj velik b .
Na koncu se izracunamo dolzino zatica l in s pomocjo polj izberemo standardno dolzino zatica.
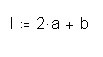
5.2 Prednastavitev vrednosti faktorjev transformacij - inicializacija
Funkcija inicializacija sluzi zato, da se faktorji oz. komponente skaliranja, transformiranja postavijo v zacetni polozaj oz. dobijo prednastavljene vrednosti. Komponente vektorja ni predstavlja nagib vektorja normale. Komponente vektorja k predstavljajo zacetno rotacijo slike v prostoru. Offsetx in offsety so koordinate polozaja zacetnega izrisa slike. Skal je faktor povecave.Funkcija za inicializacijo:
function init()
{
k[0] = 0.6123724;
k[1] = -0.5;
k[2]
= -0.6123724;
ni[0] = 0.7071068;
ni[1] = 0.0;
ni[2] = 0.7071068;
offsetx = 0.3;
offsety = 0.7;
skal = 0.5;
};
5.3 Zagon grafike
Funkcija zazene potrebne ukaze za prednastavitev graficne slike.function startgrafika()
{
var
WorkstnID = 1;
var ConnID = document.Phigs;
var WorkstnType = PWODSX;
var tone = 1;
popen_phigs("stderr", 0);
popen_ws(WorkstnID,
ConnID, WorkstnType);
popen_struct(tone);
};
5.4 Funkcije, ki dolocajo zaporedje podprogramov
Funkcije se klice ob pritisku na gumb (Izris,Reset). Sestavljajo jih ukazi za branje zacetnih parametrov in podprogrami. Pomembno pri teh funkcijah je pravilni redosled podfunkcij (podprogramov, funkcij), ki jih klicemo.5.5 Izris slike, lokalnega in globalnega koodinatnega sistema
Pri izrisu slike najprej pripravimo lokalni koordinatni sistem (x',y',z'), pri katerem velikost koordinatnih osi zavisi od premera pesta in dolzine gredi, zaradi sorazmerja pri izrisu slike. Nato izrisemo globalni koordinatni sistem (osi X,Y,Z). Osi globalnega koordinatnega sistema vedno mirujejo, medtem ko se lokalne koordinatne osi translirajo, rotirajo in skalirajo skupaj z objektom teh transformacij.
5.6 Izris vilic, bata in zatica
Najprej določimo vektorja e1 in e2. Dolocimo jima dolzino, ki
je enaka radiju kroga. Oddaljenost posamezne tocke je sestevek posameznih
vektorjev e1 in e2. Vse ostale tocke na krogu pa dobimo z FOR
zanko, ki tece od od 0 do 360 stopinj s korakom p. Tako izrisemo dva kroga, ki
sta medsebojno oddaljena za doloceno razdaljo(dolzino valja) in med njima
potegemo crte na dolocen zasuk (10 0), ki predstavljajo valj.
Funkcija je odvisna od koordinate z, pozicije zacetka in konca valja, premera
valja in barve, s katero naj bo valj izrisan.
Osnovni elementi funkcije so
predstavljeni v nadaljevanju:
function zatic(z,y1,y2,d,barva)
{ nik[0] = ni[1] * k[2] - ni[2] *
k[1];
nik[1] = ni[2] * k[0] - ni[0] * k[2];
nik[2] = ni[0] * k[1] - ni[1]
* k[0];
i = 0
for (i = 0; i <= 2; i = i + 1)
{ yr1[i] = nik[i] *
y1 * skal / 200.0;
xr[i] = k[i] * d / 2 * skal / 200.0;
zr[i] = ni[i] * d
/ 2 * skal / 200.0;
zc[i] = ni[i] * z * skal / 200.0;
yr2[i] = nik[i] * y2
* skal / 200.0;}
for(p = 0.0 ; p <= 6.28 + q ; p = p + q)
{ tx1 =
offsetx + yr1[1] + Math.cos(p) * xr[1] + Math.sin(p) * zr[1] + zc[1];
ty1 =
offsety + yr1[2] + Math.cos(p) * xr[2] + Math.sin(p) * zr[2] + zc[2];
tx2 =
offsetx + yr2[1] + Math.cos(p) * xr[1] + Math.sin(p) * zr[1] + zc[1];
ty2 =
offsety + yr2[2] + Math.cos(p) * xr[2] + Math.sin(p) * zr[2] + zc[2];
pts1[i]
= new Ppoint(notx(tx1), noty(ty1));
pts2[i] = new Ppoint(notx(tx2),
noty(ty2));
i = i + 1;
if ( i >= a )
{ line[0] = new Ppoint
(notx(tx1),noty(ty1));
line[1] = new Ppoint
(notx(tx2),noty(ty2));
slika_valj = new
Ppoint_list(2,line);
pset_line_colr_ind(barva);
ppolyline(slika_valj);
a
= a + 3; };
};
slika_krog1 = new Ppoint_list(i,
pts1);
pset_line_colr_ind(barva);
ppolyline(slika_krog1);
slika_krog2
= new Ppoint_list(i,
pts2);
pset_line_colr_ind(barva);
ppolyline(slika_krog2);
};
5.7 Skaliranje
Funkcija skaliranja omogoča povecavo ali pomanjsavo. Pri tem se skalirni
faktor spreminja - poveča ali pomanjša. function
povecaj(z)
{
skal = skal * z;
narisi();
};
function
pomanjsaj(z)
{
skal = skal / z;
narisi();
};
5.8 Translacija
Funkcija translacije je izvedena tako, da se spreminjata spremenljivki
pozicije offsetx in offsety, ki predstavljata pomik v horizontalni in vertikalni
smeri po ekranu. Spodaj predstavljena funkcija je translacija v X, Y ali Z smeri
globalnega koordinatnega sistema. Koeficienta pred faktorjem z predstavljata
smer translacije glede na koordinate globalnega koordinatnega sistema.
function translacija(form,z)
{
if
(form.tros[0].checked)
{
offsetx = offsetx - 0.5 * z / 200.0;
offsety =
offsety - 0.6123724 * z / 200.0;
}
if
(form.tros[1].checked)
{
offsetx = offsetx + 0.8660254 * z /
200.0;
offsety = offsety - 0.3535534 * z / 200.0;
}
if
(form.tros[2].checked)
{
offsety = offsety + 0.7071068 * z /
200.0;
}
narisi();
5.9 Rotacija
Pri rotaciji izracunamo nov vektor v, ki je zamaknjen za določen kot
okoli osi, okoli katere rotiramo (vektorja ni). Nato vektorju k
določimo nov polozaj, ki je enak vektorju v. Dobljeni vektor k v
novem polozaju je osnova za izris slike. 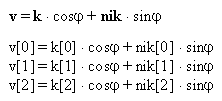
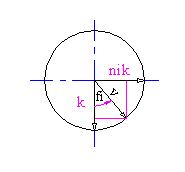
Funkcija za
rotacijo:function rotacija(form,fi)
{
var nik = new
Array();
var v = new Array();
var i;
var rad;
rad = 6.28318531 *
fi / 360.0;
nik[0] = ni[1] * k[2] - ni[2] * k[1];
nik[1] = ni[2] *
k[0] - ni[0] * k[2];
nik[2] = ni[0] * k[1] - ni[1] *
k[0];
if(form.os[0].checked) //z
{
k[0] = k[0] * Math.cos(rad) + nik[0]
* Math.sin(rad);
k[1] = k[1] * Math.cos(rad) + nik[1] *
Math.sin(rad);
k[2] = k[2] * Math.cos(rad) + nik[2] *
Math.sin(rad);
};
if(form.os[1].checked) //x
{
ni[0] = ni[0] *
Math.cos(rad) - nik[0] * Math.sin(rad)
ni[1] = ni[1] * Math.cos(rad) - nik[1]
* Math.sin(rad)
ni[2] = ni[2] * Math.cos(rad) - nik[2] *
Math.sin(rad)
};
if(form.os[2].checked) //y
{ for(i = 0; i <= 2;
i = i + 1)
{
v[i] = ni[i] * Math.cos(rad) + k[i] * Math.sin(rad);
k[i]
= k[i] * Math.cos(rad) - ni[i] * Math.sin(rad);
ni[i] =
v[i];
}
};
narisi();
};
5.10 Kontrola tock znotraj obmocja slike
Funkciji kontrolirata, ce so izracunane tocke, ki so vhodni parameter funkcije, znotraj izrisljivega obmocja. Ce so, potem funkcija vrne izhodne parametre enake vhodnim, drugace pa vrne robne tocke izrisljivega obmocja.
function notx(x)
{
if (maxx < x) maxx = x;
if (minx > x)
minx = x;
return x;
};
function noty(y)
{
if (maxy < y)
maxy = y;
if (miny > y) miny = y;
return y;
};
5.11 Resetiranje oz. postavitve slike v zacetni
polozaj
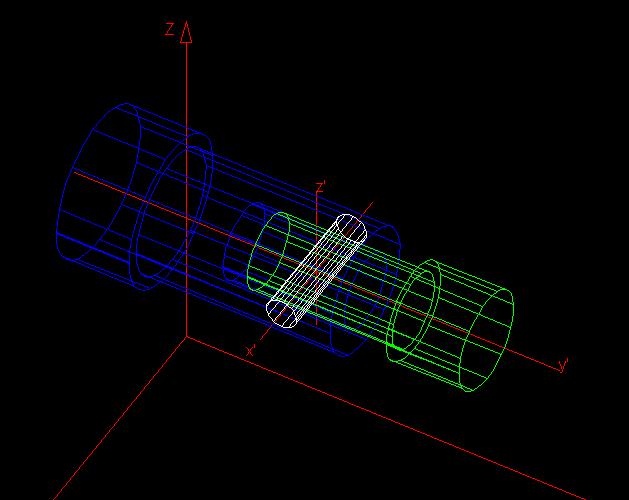
Funkcija resetiranja sluzi zato, da se slika izrise v
zacetnem polozaju. Prikazana je slika v zacetnem polozaju in funkcija za reset.
function
resetiraj()
{
init();
narisi();
};
6.0 Zagon programa
- ZAGON PROGRAMA
7.0 Zakljucek
Programiranje v Javascript-u je enostavno, ce uporabljas veliko dodatnih ordij,
ki javljajo napake in ti omogocajo tudi pomoc. Sam tega nisem imel, zato mi je vsaj v zacetku
programiranje v Javascript-u povzrocalo precej tezav. Zelo zamudna in neznana je grafika, saj
sem moral preuciti veliko primerov preden sem zastopil kako poteka programiranje grafike
s pomocjo graficne knjiznice PHIGS.
Izracun ni posebno zahteven, le izbira standardne dolzine in premera zatica je
bila bolj zamudna in se to zaradi napak v sintaksi.
Programiranje grafike je zamudno in zahteva veliko natancnost in
koncentracijo, da ne ustvarjas nepotrebnih napak.
Negastrn, avgust 2000