Fakulteta za strojništvo
Laboratorij za CAD-LECAD
Mentor: Roman Žavbi
Ljubljana, avgust 2000
Kazalo vsebine:
In the first part of the seminar there is represented a simple calculation of perch and pin for torsian charge.
Secont part of the seminar is a graphical representation of 3D-calculated part with the support of grapichal library PHIGS. Some basic geometrical transforamtions are allowed, such as rotation, scaling and translation.
Namen izdelave programa je rešitev konkretnega primera iz strojništva in hrati spoznavanje teoretičnih osnov glede 3D transformacij ter spoznavanje programskega jezika HTML, Javascript in graficne knjiznice PHIGS. Uporaba HTML-ja je v zadnjem casu vedno več v uporabi, predvsem zaradi interneta. S HTML in Javascript-om lahko sami oblikujemo spletne strani na internetu in na njih izvajamo želene programe.
Izdelajte računalniški program za kontrolo valjastega zatiča (DIN 7), ki je obremenjen s torzijskim momentom. Vhodni podatki so moč, ki jo gredna vez prenaša, materiala gredi in pesta. Premer gredi določite po poenostavljeni formuli za torzijsko obremenjene gredi. Klasične tabele oblikujte kot datoteke. Upoštevajte statične in dinamične obremenitve.
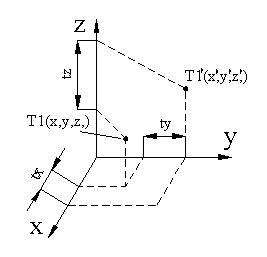
Grafični del programa naj prikaže žični model kontroliranega sklopa po sliki, z vsemi kotami. Funkcionalni deli maj bodo različnih barv. Omogoči naj tudi tri osnovne geometrijske transformacije: rotacijo, translacijo in skaliranje. Vnos transformacijskih parametrov naj bo izveden preko enostavnega menuja. Objekt transformiranja naj bo sklop z zaticem brez kot in kotirnih črt.

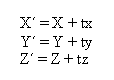
Običajno se rotacija izvaja okrog določene osi. Spodaj predstavljena rotacija je okrog Z-osi. Princip za ostali dve transformaciji je isti le transformacijski matriki se razlikujeta predstavljeni sta v točki zapis transformacij v homogenih koordinatah (rotacija).
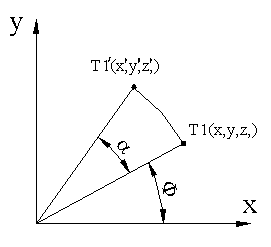
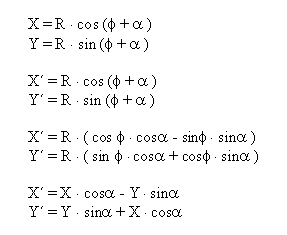
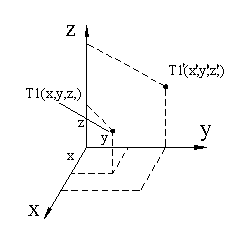
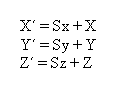
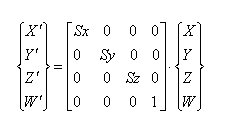
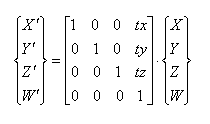
a) okoli X osi:
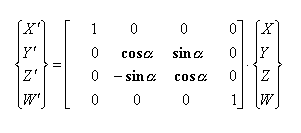
b) okoli Y osi:
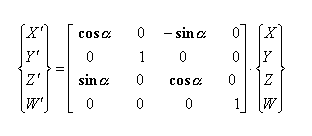
c) okoli Z osi:
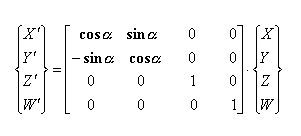

Pri preračunu sklopa sem uporabil standard DIN 7, ki določa dimenzije, materiale, dopustne obremenitve zatičev ter druge standarde, ki določajo materiale in dopustne obremenitve za materiale gredi in peste. Pri preračunu gredi pa sem upošteval še vpliv luknje zatiča na koncentracijo napetosti. Pri tem sem določil dodatni pogoj, da mora biti premer gredi vsaj trikrat večji od premera zatiča, material zatiča pa mora biti vedno za razred boljši od materiala gredi in peste.
Uporabnost programa pri preračunu sklopa je omejena na standardne dimenzije zatičev, premerov od 0.8 do 100 mm in dolžine do 320 mm. Tak sklop lahko prenaša že zelo velik moment, čeprav je za take momente gotovo primernejša druga oblika gredne vezi.
Pri izdelavi programa nisem uporabljal zgoraj predstavljenih teoretičnih osnov o transformacijah, uporabil pa sem poenostavljeno teorijo 3D transformacij.
Najprej določimo dva vektorja e1 in e2 katerima določimo dolžino, ki je enaka radiju kroga. Oddaljenost posamezne točke dobimo tako, da seštejemo posamezne komponente vektorjev e1 in e2. Vse ostale točke pa dobimo tako, da v programu uporabimo funkcijo, ki spreminja kot od 0 do 360 po koraku p. Del programa, ki določi razdalje tock tx in ty je predstavljen v spodnji enacbi
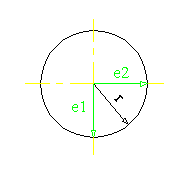
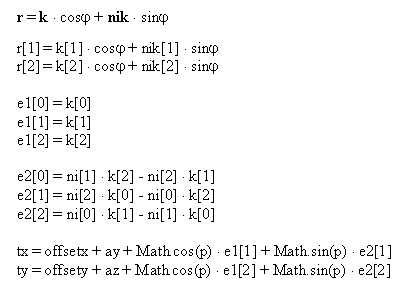
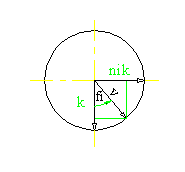
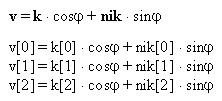
Funkcija translacije je izvedena tako, da se spreminjata spremenljivki, ki predstavljata pomik lokalnega koordinatnega sistema v horizontalni in vertikalni smeri ekrana glede na globalni oziroma fiksni koordinatni sistem. Isti spremenljivki vplivata tudi na translacijo sklopa na skici.