

In the first part of the seminar there is represented a simple calculation of perch
and stick for torsian charge.
Secont part of the seminar is a graphical representation of 3D-calculated part with
the support of grapichal library PHIGS. Some basic geometrical transforamtions
are allowed, such as rotation, scaling and translation.
Namen izdelave programa za izris in preracun valjastega zatica po DIN 7 je spoznavanje teoretičnih osnov glede 3D transformacij ter spoznavanje programskega jezika HTML, Javascript in graficne knjiznice PHIGS.
Izdelajte racunalniski program za kontrolo valjastega zatica (DIN 7), ki je obremenjen s torzijskim momentom. Vhodni podatki so moc, ki jo gredna vez prenasa, materiala gredi in pesta. Premer gredi dolocite po poenostavljeni formuli za torzijsko obremenjene gredi. Klasicne tabele oblikujte kot datoteke. Upostevajte staticne in dinamicne obremenitve.
Graficni del programa naj prikazuje 3D zicni model sklopa na sliki. Funkcionalni deli naj bodo razlicnih barv. Omogoci naj tudi tri osnovne geometrijske transformacije: rotacijo, translacijo in skaliranje. Vnos transformacijskih parametrov naj bo izveden preko enostavnega menuja. Objekt transformiranja naj bo sklop z zaticem brez kot in kotirnih crt.
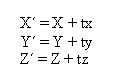

Običajno se rotacija izvaja okrog določene osi. Spodaj
predstavljena rotacija je okrog Z-osi. Princip za ostali dve transformaciji je
isti le transformacijski matriki se razlikujeta predstavljeni sta v točki zapis
transformacij v homogenih koordinatah (rotacija).
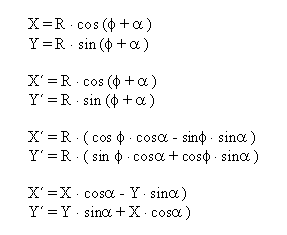

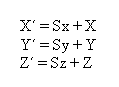

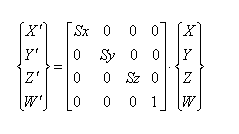
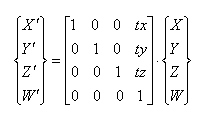
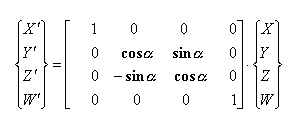
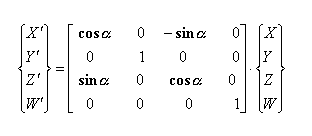
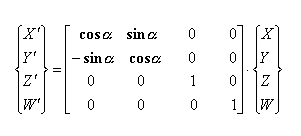
Program je zgrajen s pomočjo 16 funkcij oz. podprogramov:
- Izracun premera gredi [izracun_gredi]
- Izracun premera zatica [izracun]
- Prednastavitev vrednosti faktorjev transformacij - inicializacija [init]
- Zagon grafike [startgrafika]
- Funkcije, ki dolocajo zaporedje podprogramov [narisi,izrisvsega]
- Izris slike, lokalnega in globalnega koodinatnega sistema[slika]
- Izris valjev [krogy]
- Skaliranje [povecaj,pomanjsaj ]
- Translacija [translacija]
- Rotacije [rotacija]
- Kontrola tock znotraj obmocja slike [notx, noty]
- Resetiranje oz. postavitve slike v zacetni polozaj [resetiraj]
- Izpis izracuna in vhodnih podatkov v novo okno v urejeni obliki [izpisvokno]

Izracunani premer gredi se zaokrozi na prvi standardni premer gredi. Standardni premeri gredi so zapisani v datoteki standard.js in jih preberemo ob zagonu strani.
Izracun premera zatica poteka po dveh poteh. Prva pot je izracun premera zatica glede
na dopustni tlak, druga pa glede na dopustno strizno napetost.
Izberemo najvecji izracunani premer od obeh poti in ga zaokrozimo, tako kot gred,
na standardni premer.
Enacba za izracun premera zatica glede na dopustni tlak:
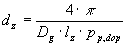
Enacba za izracun premera zatica glede na dopustno strizno napetost zatica:

Funkcija za inicializacijo:
function init()
{
k[0] = 0.6123724;
k[1] = -0.5;
k[2] = -0.6123724;
ni[0] = 0.7071068;
ni[1] = 0.0;
ni[2] = 0.7071068;
offsetx = 0.3;
offsety = 0.7;
skal = 0.5;
};
function startgrafika()
{
var WorkstnID = 1;
var ConnID = document.Phigs;
var WorkstnType = PWODSX;
var tone = 1;
popen_phigs("stderr", 0);
popen_ws(WorkstnID, ConnID, WorkstnType);
popen_struct(tone);
};
Najprej določimo vektorja e1 in e2. Dolocimo jima dolzino, ki je enaka
radiju kroga. Oddaljenost posamezne tocke je sestevek posameznih vektorjev
e1 in e2. Vse ostale tocke na krogu pa dobimo z FOR zanko, ki tece
od od 0 do 360 stopinj s korakom p.
Tako izrisemo dva kroga, ki sta medsebojno oddaljena za doloceno razdaljo(dolzino valja)
in med njima potegemo crte na dolocen zasuk (10 0), ki predstavljajo valj.
Funkcija je odvisna od koordinate z, pozicije zacetka in konca valja, premera valja in barve,
s katero naj bo valj izrisan.
Osnovni elementi funkcije so predstavljeni v nadaljevanju:
function krogy(z,y1,y2,d,barva)
{ nik[0] = ni[1] * k[2] - ni[2] * k[1];
nik[1] = ni[2] * k[0] - ni[0] * k[2];
nik[2] = ni[0] * k[1] - ni[1] * k[0];
i = 0
for (i = 0; i <= 2; i = i + 1)
{ yr1[i] = nik[i] * y1 * skal / 200.0;
xr[i] = k[i] * d / 2 * skal / 200.0;
zr[i] = ni[i] * d / 2 * skal / 200.0;
zc[i] = ni[i] * z * skal / 200.0;
yr2[i] = nik[i] * y2 * skal / 200.0;}
for(p = 0.0 ; p <= 6.28 + q ; p = p + q)
{ tx1 = offsetx + yr1[1] + Math.cos(p) * xr[1] + Math.sin(p) * zr[1] + zc[1];
ty1 = offsety + yr1[2] + Math.cos(p) * xr[2] + Math.sin(p) * zr[2] + zc[2];
tx2 = offsetx + yr2[1] + Math.cos(p) * xr[1] + Math.sin(p) * zr[1] + zc[1];
ty2 = offsety + yr2[2] + Math.cos(p) * xr[2] + Math.sin(p) * zr[2] + zc[2];
pts1[i] = new Ppoint(notx(tx1), noty(ty1));
pts2[i] = new Ppoint(notx(tx2), noty(ty2));
i = i + 1;
if ( i >= a )
{ line[0] = new Ppoint (notx(tx1),noty(ty1));
line[1] = new Ppoint (notx(tx2),noty(ty2));
slika_valj = new Ppoint_list(2,line);
pset_line_colr_ind(barva);
ppolyline(slika_valj);
a = a + 3; };
};
slika_krog1 = new Ppoint_list(i, pts1);
pset_line_colr_ind(barva);
ppolyline(slika_krog1);
slika_krog2 = new Ppoint_list(i, pts2);
pset_line_colr_ind(barva);
ppolyline(slika_krog2);
};
Funkcija skaliranja omogoča povecavo ali pomanjsavo.
Pri tem se skalirni faktor spreminja - poveča ali
pomanjša.
function povecaj(z)
{
skal = skal * z;
narisi();
};
function pomanjsaj(z)
{
skal = skal / z;
narisi();
};
Funkcija translacije je izvedena tako,
da se spreminjata spremenljivki pozicije offsetx in offsety, ki
predstavljata pomik v horizontalni in vertikalni smeri po ekranu. Spodaj
predstavljena funkcija je translacija v X, Y ali Z smeri globalnega koordinatnega
sistema. Koeficienta pred faktorjem z predstavljata smer translacije glede na
koordinate globalnega koordinatnega sistema.
function translacija(form,z)
{
if (form.tros[0].checked)
{
offsetx = offsetx - 0.5 * z / 200.0;
offsety = offsety - 0.6123724 * z / 200.0;
}
if (form.tros[1].checked)
{
offsetx = offsetx + 0.8660254 * z / 200.0;
offsety = offsety - 0.3535534 * z / 200.0;
}
if (form.tros[2].checked)
{
offsety = offsety + 0.7071068 * z / 200.0;
}
narisi();
Pri rotaciji izracunamo nov vektor v, ki je zamaknjen za določen
kot okoli osi, okoli katere rotiramo (vektorja ni).
Nato vektorju k določimo nov
polozaj, ki je enak vektorju v. Dobljeni vektor k v novem polozaju
je osnova za izris slike.
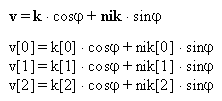
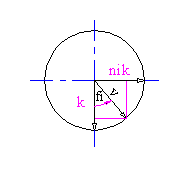
Funkcija za rotacijo:
function rotacija(form,fi)
{
var nik = new Array();
var v = new Array();
var i;
var rad;
rad = 6.28318531 * fi / 360.0;
nik[0] = ni[1] * k[2] - ni[2] * k[1];
nik[1] = ni[2] * k[0] - ni[0] * k[2];
nik[2] = ni[0] * k[1] - ni[1] * k[0];
if(form.os[0].checked) //z
{
k[0] = k[0] * Math.cos(rad) + nik[0] * Math.sin(rad);
k[1] = k[1] * Math.cos(rad) + nik[1] * Math.sin(rad);
k[2] = k[2] * Math.cos(rad) + nik[2] * Math.sin(rad);
};
if(form.os[1].checked) //x
{
ni[0] = ni[0] * Math.cos(rad) - nik[0] * Math.sin(rad)
ni[1] = ni[1] * Math.cos(rad) - nik[1] * Math.sin(rad)
ni[2] = ni[2] * Math.cos(rad) - nik[2] * Math.sin(rad)
};
if(form.os[2].checked) //y
{ for(i = 0; i <= 2; i = i + 1)
{
v[i] = ni[i] * Math.cos(rad) + k[i] * Math.sin(rad);
k[i] = k[i] * Math.cos(rad) - ni[i] * Math.sin(rad);
ni[i] = v[i];
}
};
narisi();
};
Funkciji kontrolirata, ce so izracunane tocke, ki so vhodni parameter funkcije, znotraj izrisljivega obmocja. Ce so, potem funkcija vrne izhodne parametre enake vhodnim, drugace pa vrne robne tocke izrisljivega obmocja.
function notx(x)
{
if (maxx < x) maxx = x;
if (minx > x) minx = x;
return x;
};
function noty(y)
{
if (maxy < y) maxy = y;
if (miny > y) miny = y;
return y;
};

function resetiraj()
{
init();
narisi();
};
");
function izpisvokno()
{
Okno=window.open("","Rezultati","width=450,height=300,resizable=yes,scrollbars=yes");
Okno.document.write("
Okno.document.write("");
Okno.document.write("Izracun zatica:
Okno.document.write("Vrtilni moment T = " + document.podatki.T.value + " Nm");
Okno.document.write("Dopustna torzijska napetost gredi ttg= " + document.podatki.Ttg.value + " N/mm2");
Okno.document.write("Premer gredi Dg = " + document.podatki.dg.value + " mm");
Okno.document.write("Dopustni tlak pesta glede na obremenitev pp,dop= " + document.podatki.pp.value + " N/mm2");
Okno.document.write("Dopustna strizna napetost zatica tsz,dop= " + document.podatki.Tsz.value + " N/mm2");
Okno.document.write("Dolzina pesta lp= " + document.podatki.lp.value + " mm");
Okno.document.write("Premer pesta dp= " + document.podatki.dp.value + " mm");
Okno.document.write("Premer zatica dz= " + document.podatki.dz.value + " mm");
Okno.document.write("");
};
Izracun premera gredi in premera zatica je bil zelo enostaven, saj so pri izracunu bile uporabljene enacbe za poenostavljen izracun le-teh.
Tezji del naloge je bila izdelava slike sklopa gredi, pesta in zatica v 3D. Ker sintakse Javascript od prej nisem poznal, sem se moral s to najprej seznaniti. Ravno tako nisem poznal ukazov za delo z graficno knjiznico Phigs, sem pa imel na razpolago nekaj primerov, kjer je bila le-ta uporabljena. Tako je bilo zacetno spoznavanje mnogo lazje.
Pri izdelavi slike sem uporabil prirejeno oz. poenostavljeno teorijo 3D transformacij in z njo povezane transformacijske matrike (translacije, rotacije in skaliranje), Osnova za določitev tocke in lege slike so trije vektorji ni, k, nik. Začetni položaj vektorjev ni in k je predhodno določen, tretji vektor nik pa je vektorski produkt vektrja ni in k. Program ne uporablja enega polja v katerem so zapisane vse točke, ki jih pri posamezni taranformaciji vsako posebej na novo izračuna, ampak se točke vsakokrat na novo izračunajo glede na položaj treh vektorjev in se sproti tudi povežejo.
Funkcije v programu sem poskusal cim bolj posplositi, toda kljub temu sem pazil na mejo razumljivosti in enostzavnosti le-teh, saj program ni zelo obsiren in je namenjen zelo ozkemu delu uporabe. Ce bi bile funkcije externe in bi se lahko uporabljale tudi v drugih programih, bi se jih verjetno dalo se bolj poenostaviti in posplositi.
