Aksialni sodčasti ležaj

Kazalo:

1. Abstract
2. Uvod
3. Definicija naloge
4. Teoretične osnove
5. Potek izdelave in opis programa:
Izvorna koda programa
6. Zakljucek
7. Literatura
8. Zagon programa

1. Abstract

This document presents some basics of 2D geometrics. Main properties are translation, rotation and scalation in X - Y field. For this presentation is used graphics library Phigs.

2. Uvod

Bistvo naloge je bilo vezano na samostojno programiranje v dolocenem programskem jeziku. Student je moral osvojiti znanje uporabe transformacijskih matrik za premikanje (translacija), skaliranje in rotacijo prikazanih elementov, torej transformacije v 2D ravnini.

3. Definicija naloge

Program naj prilaže aksialni sodčkasti ležaj. Omogoča naj izbor ležaja glede na premer gredi iz seznama in prikaz
le tega v narisu. Program mora omogočati tudi translacijo rotacijo in skaliranje izbranega ležaja.

4. Teoretične osnove

4.1. Graficni in formularni zapis 2D transformacij

a.) Translacija

b.) Rotacija

c.) Skaliranje

4.2 Matricni zapis 2D transformacij

4.2.1 Translacija

a) Kartezijeve koordinate: ni mozno zapisati v matricnem nacinu

b) Homogene koordinate:

4.2.2 Rotacija

a) Kartezijeve koordinate:

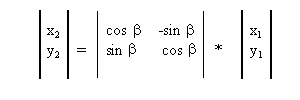
b) Homogene koordinate:

4.2.3. Skaliranje:

a) Kartezijeve koordinate:

b) Homogene koordinate:

5. Potek izdelave in opis programa:

Program je sestavljen predvsem iz dveh delov; iz vnosnega dela (javascript) in grafičnega dela (javascript + knjižnice phigsa).
Podatke za izris ležaja program prebira s pomočjo funkcije za branje iz datoteke - baze podatkov (v mojem primeru je ime datoteke: podat.js). Prebrane podatke program pretvori z nekim faktorjem, ki je potreben, da se bo vijak izrisal v določenem velikostnem območju.
Sledi funkcija, ki glede na podano izhodiščno točko in z prebranimi podatki izračuna posamezne točke ležaja. Izračunane točke lahko z funkcijo za transformacijo transformiramo.

6. Zaključek

Pri izdelavi programa sem spoznal osnovne elemente programiranja v JavaScriptu in JavaScriptu z dodatkom knjižnic iz Phigsa, seznanil pa sem se tudi z osnovnimi geometrijskimi transformacijami v ravnini.
Pri izdelavi programa sem se, kot sem že omenil, držal oblike programa pri kateri je program sestavljen iz posameznih funkcij. Kljub temu da sem čimveč programiral z polji je končni program dokaj dolg in počasen.
Če bi hotel program popolnoma zoptimirati bi se mogel posvetiti programiranju v C++.

7. Literatura

1. Jože Hrženjak; Spoznavanje strojnih elementov
2. Peter Hribar; SPOZNAJMO JAVASCRIPT; Flamingo 1998

<html>
<head>
<TITLE>Ležaj TSA</TITLE>
<META HTTP-EQUIV="Content-Type" CONTENT="text/html; charset=UTF-8">
</head>
<body BGCOLOR="#FFFFFF">
<CENTER><h2>LeĹľaj TSA</h2>

<TABLE BORDER WIDTH="900">
<TR> <TD ALIGN=CENTER VALIGN=CENTER WIDTH="100%" HEIGT="100%">
<b>Izbira leĹľaja:</b><br><br>
<FORM NAME="seznam">

<b>Izris leĹľaja:</b><br><br>
<INPUT type="button" value=" Naris leĹľaja " onclick="(naris('0',index(this.form),0,1,0,0))"><br><br>
<b>Translacija leĹľaja</b><br><br>
Premakni za: <INPUT type="text" NAME="tran" VALUE=20 SIZE=4>mm<br><br>
<INPUT type="button" value=" Gor "
onclick="(naris('PY', index(this.form), 0, 1, 0, this.form.tran.value))"><br>
   <INPUT type="button" value=" Levo "
onclick="(naris('PX',index(this.form),0,1, -this.form.tran.value,0))">
       
<INPUT type="button" value=" Desno "
onclick="(naris('PX',index(this.form),0,1, this.form.tran.value, 0))"><br>
<INPUT type="button" value=" Dol "
onclick="(naris('PY',index(this.form),0,1,0,-this.form.tran.value))"><br><br>

<b>Rotacija leĹľaja:</b><br><br>
Rotiraj za: <INPUT type="text" NAME="rot" VALUE=45 SIZE=6>°<br><br>
<INPUT type="button" value=" V levo "
onclick="(naris('R',index(this.form),this.form.rot.value,1,0,0))"><br><br>
<INPUT type="button" value="V desno "
onclick="(naris('R',index(this.form),-this.form.rot.value,1,0,0))"><br><br>

<b>Skaliranje leĹľaja:</b><br><br>
Skaliraj: <INPUT type="text" NAME="skal" VALUE=2 SIZE=6><br><br>
<INPUT type="button" value=" povečaj "
onclick="(naris('S',index(this.form),0,this.form.skal.value,0,0))"><br><br>
<INPUT type="button" value="pomanjšaj"
onclick="(naris('S',index(this.form),0,(1/this.form.skal.value),0,0))"><br><br>
</FORM>
</TD>
<TD>

<applet code=Phigs.class codebase="." archive=phigs.jar name=Phigs width=700 height=700>
</applet>

<script language=javascript src="phigs.js"></script>
<script language=javascript src="podat.js">
document.write("Ne morem naloĹľiti podtakov iz datoteke podat.js")
</script>

var M=3/500;
var tocke=new Array();
var t=new Array();
var dsx=0.15;
var dsy=0.65;
var sx=0;
var sy=0;

var radiani=Math.PI/180;
var lok=new Array();
var lok_d=new Array();
var lok_lz=new Array();
var lok_dz=new Array();
var lokst,lokst_d,lokst_lz,lokst_dz;
var izr=0;

// Koordinatni križ
function koordinate()
{

var ko=new Array();

ko[0]=new Ppoint(0.02, 0.95);
ko[1]=new Ppoint(0.015, 0.95);
ko[2]=new Ppoint(0.02, 0.98);
ko[3]=new Ppoint(0.025, 0.95);
ko[4]=new Ppoint(ko[0].x, ko[0].y);

ko[5]=new Ppoint(0.02, 0.02);
ko[6]=new Ppoint(0.95, 0.02);
ko[7]=new Ppoint(0.95, 0.015);
ko[8]=new Ppoint(0.98, 0.02);
ko[9]=new Ppoint(0.95, 0.025);
ko[10]=new Ppoint(ko[6].x, ko[6].y);

var kr=new Ppoint_list(11, ko);

pset_line_colr_ind(2);
pset_text_colr_ind(2);
ptext(new Ppoint(0.04, 0.93), "Y");
ptext(new Ppoint(0.93, 0.04), "X");
ppolyline(kr);
}

function index(form) {
return (form.lezaj.selectedIndex);
}

// Funkcija za risanje lokov
/*
t - Array, tu so shranjene tocke loka
x0,y0 - sredisce
r - radij
dk - delta kota
zk - zacetni kot
k - kot
*/
function Radij(t,x0, y0, r, dk, zk, k)
{
for(j=0; j<=k/dk; j++)
{
t[j]=new Ppoint();
t[j].x=x0+Math.cos((zk+dk*j)*radiani)*r;
t[j].y=y0+Math.sin((zk+dk*j)*radiani)*r;
}
return k/dk+1;

}

// Funkcija za skaliranje, trnslacijo in rotiranje
function Transformacija(kotr,ska,trax,tray)
{
var x2,y2;
var xr=tocke[2].x;
var yr=tocke[2].y;

trax=trax*M;
tray=tray*M;

for(var i=0; i<tocke.length; i++){
x2=(tocke[i].x-xr)*Math.cos(kotr*radiani)-(tocke[i].y-yr)*Math.sin(kotr*radiani);
y2=(tocke[i].x-xr)*Math.sin(kotr*radiani)+(tocke[i].y-yr)*Math.cos(kotr*radiani);
x2=x2*ska+xr+trax;
y2=y2*ska+yr+tray;
tocke[i]=new Ppoint(x2, y2);
}

for (i=0;i<lok.length;i++)
{
x2=(lok[i].x-xr)*Math.cos(kotr*radiani) - (lok[i].y-yr)*Math.sin(kotr*radiani);
y2=(lok[i].x-xr)*Math.sin(kotr*radiani) + (lok[i].y-yr)*Math.cos(kotr*radiani);
x2=x2*ska+xr+trax;
y2=y2*ska+yr+tray;
lok[i]=new Ppoint(x2,y2);
}

for (i=0;i<lok_d.length;i++)
{
x2=(lok_d[i].x-xr)*Math.cos(kotr*radiani) - (lok_d[i].y-yr)*Math.sin(kotr*radiani);
y2=(lok_d[i].x-xr)*Math.sin(kotr*radiani) + (lok_d[i].y-yr)*Math.cos(kotr*radiani);
x2=x2*ska+xr+trax;
y2=y2*ska+yr+tray;
lok_d[i]=new Ppoint(x2,y2);
}

for (i=0;i<lok_dz.length;i++)
{
x2=(lok_dz[i].x-xr)*Math.cos(kotr*radiani) - (lok_dz[i].y-yr)*Math.sin(kotr*radiani);
y2=(lok_dz[i].x-xr)*Math.sin(kotr*radiani) + (lok_dz[i].y-yr)*Math.cos(kotr*radiani);
x2=x2*ska+xr+trax;
y2=y2*ska+yr+tray;
lok_dz[i]=new Ppoint(x2,y2);
}

for (i=0;i<lok_lz.length;i++)
{
x2=(lok_lz[i].x-xr)*Math.cos(kotr*radiani) - (lok_lz[i].y-yr)*Math.sin(kotr*radiani);
y2=(lok_lz[i].x-xr)*Math.sin(kotr*radiani) + (lok_lz[i].y-yr)*Math.cos(kotr*radiani);
x2=x2*ska+xr+trax;
y2=y2*ska+yr+tray;
lok_lz[i]=new Ppoint(x2,y2);
}

}

// Izračuna vse potrebne točke
function Izracun(z)
{
izr=1;
for(var i=0; i<=13; i++)
{
t[i]=podatki[z][i]*M;
}

skrogx=sx+t[1]/2;
skrogy=sy+t[3]+t[4];

var tock1x=skrogx+Math.cos((224+2*0)*radiani)*t[2];
var tock1y=skrogy+Math.sin((224+1*0)*radiani)*t[2];
var tock2x=skrogx+Math.cos((224+2*46)*radiani)*t[2];
var tock2y=skrogy+Math.sin((224+2*46)*radiani)*t[2];

//tocke[0]=new Ppoint(tock1x+(tock1x-sx),tock1y);
tocke[0]=new Ppoint(tock1x+((tock1x*(13/16))-sx),sy+t[7]);
tocke[1]=new Ppoint(sx, sy+t[7]);
tocke[2]=new Ppoint(sx, sy);
tocke[3]=new Ppoint(sx+t[1], sy);
tocke[4]=new Ppoint(sx+t[1], sy+t[7]);
tocke[5]=new Ppoint(t[1]-(28/16)*(t[1]-tock2x),sy+t[7]);

tocke[6]=new Ppoint(sx+(t[1]-t[6])/2,sy);
tocke[7]=new Ppoint(sx+(t[1]-t[6])/2,sy+t[10]);
tocke[8]=new Ppoint(tocke[7].x+t[6],tocke[7].y);
tocke[9]=new Ppoint(tocke[8].x,sy);

var tc1x=(t[1]-t[5])/2;
var tc2x=(t[5]-t[0])/2;

tocke[10]=new Ppoint(sx+tc1x, sy+t[3]);
tocke[11]=new Ppoint(tocke[10].x+tc2x, sy+t[3]);
tocke[12]=new Ppoint(tocke[11].x,tocke[11].y-t[8]);

tocke[13]=new Ppoint(tocke[12].x+t[0], tocke[12].y);

tocke[14]=new Ppoint(tocke[13].x, tocke[13].y+t[8]);
tocke[15]=new Ppoint(tocke[14].x+tc2x, tocke[14].y);

tocke[16]=new Ppoint(tocke[14].x, tocke[14].y);
tocke[17]=new Ppoint(tocke[11].x, tocke[11].y);

lokst=Radij(lok,skrogx,skrogy,t[2],1,224,19);
lokst_d=Radij(lok_d,skrogx,skrogy,t[2],1,297,19);
lokst_lz=Radij(lok_lz,-t[12],-t[13],t[2],1,46.5,13);

tocke[18]=new Ppoint(lok_lz[lokst_lz-1].x,lok_lz[lokst_lz-1].y);
tocke[19]=new Ppoint(lok[3].x,lok[3].y);

tocke[20]=new Ppoint(lok_lz[0].x,lok_lz[0].y);
tocke[21]=new Ppoint(lok[lokst-4].x,lok[lokst-4].y);

lokst_dz=Radij(lok_dz,t[1]+t[12],-t[13],t[2],1,120,13);

tocke[22]=new Ppoint(lok_lz[0].x,lok_lz[0].y);
tocke[23]=new Ppoint(lok_dz[lokst_dz-1].x,lok_dz[lokst_dz-1].y);

tocke[24]=new Ppoint(lok_dz[0].x,lok_dz[0].y);
tocke[25]=new Ppoint(lok_d[16].x,lok_d[16].y);

tocke[26]=new Ppoint(lok_dz[lokst_dz-1].x,lok_dz[lokst_dz-1].y);
tocke[27]=new Ppoint(lok_d[3].x,lok_d[3].y);

tocke[28]=new Ppoint(tocke[11].x,tocke[11].y);
tocke[29]=new Ppoint(tocke[11].x,tocke[20].y);

tocke[30]=new Ppoint(tocke[14].x,tocke[14].y);
tocke[31]=new Ppoint(tocke[14].x,tocke[23].y);

tocke[32]=new Ppoint(tocke[10].x,tocke[10].y);
tocke[33]=new Ppoint(tocke[10].x,t[3]-t[9]);

tocke[34]=new Ppoint(tocke[15].x,tocke[15].y);
tocke[35]=new Ppoint(tocke[15].x,t[3]-t[9]);

tocke[36]=new Ppoint(t[1]/2,t[3]+t[9]);
tocke[37]=new Ppoint(t[1]/2,-t[9]);

tocke[38]=new Ppoint(tocke[15].x,t[3]-t[9]);
tocke[39]=new Ppoint(t[1]-(30/16)*(t[1]-tock2x),t[3]-t[9]);

tocke[40]=new Ppoint(tocke[10].x,t[3]-t[9]);
tocke[41]=new Ppoint(tock1x+((tock1x*(15/16))-sx),tocke[40].y);

}
// Nariše lik
function Risi()
{

var tocke1=new Array;
var lok1=new Array();
var lok_d1=new Array();
var lok_lz1=new Array();
var lok_dz1=new Array();

for (var i=0; i<=41; i++)
{
tocke1[i]=new Ppoint(tocke[i].x+dsx,tocke[i].y+dsy);
}

for (i=0; i<lokst; i++)
{
lok1[i]=new Ppoint(lok[i].x+dsx,lok[i].y+dsy);
}

for (i=0; i<lokst_d; i++)
{
lok_d1[i]=new Ppoint(lok_d[i].x+dsx,lok_d[i].y+dsy);
}

for (i=0; i<lokst_lz; i++)
{
lok_lz1[i]=new Ppoint(lok_lz[i].x+dsx,lok_lz[i].y+dsy);
}

for (i=0; i<lokst_dz; i++)
{
lok_dz1[i]=new Ppoint(lok_dz[i].x+dsx,lok_dz[i].y+dsy);
}

pset_line_colr_ind(4);
var crte1_t=new Array();
crte1_t[0]= new Ppoint(tocke1[0].x, tocke1[0].y);
crte1_t[1]= new Ppoint(tocke1[1].x, tocke1[1].y);
crte1_t[2]= new Ppoint(tocke1[2].x, tocke1[2].y);
crte1_t[3]= new Ppoint(tocke1[3].x, tocke1[3].y);
crte1_t[4]= new Ppoint(tocke1[4].x, tocke1[4].y);
crte1_t[5]= new Ppoint(tocke1[5].x, tocke1[5].y);
var crte1=new Ppoint_list(6, crte1_t);
ppolyline(crte1);

var crte2_t=new Array();
crte2_t[0]= new Ppoint(tocke1[6].x, tocke1[6].y);
crte2_t[1]= new Ppoint(tocke1[7].x, tocke1[7].y);
crte2_t[2]= new Ppoint(tocke1[8].x, tocke1[8].y);
crte2_t[3]= new Ppoint(tocke1[9].x, tocke1[9].y);
var crte2=new Ppoint_list(4, crte2_t);
ppolyline(crte2);

var crte3_t=new Array();
crte3_t[0]= new Ppoint(tocke1[10].x, tocke1[10].y);
crte3_t[1]= new Ppoint(tocke1[11].x, tocke1[11].y);
crte3_t[2]= new Ppoint(tocke1[12].x, tocke1[12].y);
var crte3=new Ppoint_list(3, crte3_t);
ppolyline(crte3);

var crte3_t1=new Array();
crte3_t1[0]= new Ppoint(tocke1[13].x, tocke1[13].y);
crte3_t1[1]= new Ppoint(tocke1[14].x, tocke1[14].y);
crte3_t1[2]= new Ppoint(tocke1[15].x, tocke1[15].y);
var crte31=new Ppoint_list(3, crte3_t1);
ppolyline(crte31);

var crte4_t=new Array();
crte4_t[0]= new Ppoint(tocke1[16].x, tocke1[16].y);
crte4_t[1]= new Ppoint(tocke1[17].x, tocke1[17].y);
var crte4=new Ppoint_list(2, crte4_t);
ppolyline(crte4);

//pset_line_colr_ind(2);

var crte5_t=new Array();
crte5_t[0]= new Ppoint(tocke1[18].x, tocke1[18].y);
crte5_t[1]= new Ppoint(tocke1[19].x, tocke1[19].y);
var crte5=new Ppoint_list(2, crte5_t);
ppolyline(crte5);

var crte6_t=new Array();
crte6_t[0]= new Ppoint(tocke1[20].x, tocke1[20].y);
crte6_t[1]= new Ppoint(tocke1[21].x, tocke1[21].y);
var crte6=new Ppoint_list(2, crte6_t);
ppolyline(crte6);

var crte7_t=new Array();
crte7_t[0]= new Ppoint(tocke1[22].x, tocke1[22].y);
crte7_t[1]= new Ppoint(tocke1[23].x, tocke1[23].y);
var crte7=new Ppoint_list(2, crte7_t);
ppolyline(crte7);

var crte8_t=new Array();
crte8_t[0]= new Ppoint(tocke1[24].x, tocke1[24].y);
crte8_t[1]= new Ppoint(tocke1[25].x, tocke1[25].y);
var crte8=new Ppoint_list(2, crte8_t);
ppolyline(crte8);

var crte9_t=new Array();
crte9_t[0]= new Ppoint(tocke1[26].x, tocke1[26].y);
crte9_t[1]= new Ppoint(tocke1[27].x, tocke1[27].y);
var crte9=new Ppoint_list(2, crte9_t);
ppolyline(crte9);

var crte10_t=new Array();
crte10_t[0]= new Ppoint(tocke1[28].x, tocke1[28].y);
crte10_t[1]= new Ppoint(tocke1[29].x, tocke1[29].y);
var crte10=new Ppoint_list(2, crte10_t);
ppolyline(crte10);

var crte11_t=new Array();
crte11_t[0]= new Ppoint(tocke1[30].x, tocke1[30].y);
crte11_t[1]= new Ppoint(tocke1[31].x, tocke1[31].y);
var crte11=new Ppoint_list(2, crte11_t);
ppolyline(crte11);

var crte12_t=new Array();
crte12_t[0]= new Ppoint(tocke1[32].x, tocke1[32].y);
crte12_t[1]= new Ppoint(tocke1[33].x, tocke1[33].y);
var crte12=new Ppoint_list(2, crte12_t);
ppolyline(crte12);

var crte13_t=new Array();
crte13_t[0]= new Ppoint(tocke1[34].x, tocke1[34].y);
crte13_t[1]= new Ppoint(tocke1[35].x, tocke1[35].y);
var crte13=new Ppoint_list(2, crte13_t);
ppolyline(crte13);

var crte14_t=new Array();
crte14_t[0]= new Ppoint(tocke1[36].x, tocke1[36].y);
crte14_t[1]= new Ppoint(tocke1[37].x, tocke1[37].y);
var crte14=new Ppoint_list(2, crte14_t);
pset_line_colr_ind(2);
ppolyline(crte14);

var crte15_t=new Array();
crte15_t[0]= new Ppoint(tocke1[38].x, tocke1[38].y);
crte15_t[1]= new Ppoint(tocke1[39].x, tocke1[39].y);
var crte15=new Ppoint_list(2, crte15_t);
pset_line_colr_ind(4);
ppolyline(crte15);

var crte16_t=new Array();
crte16_t[0]= new Ppoint(tocke1[40].x, tocke1[40].y);
crte16_t[1]= new Ppoint(tocke1[41].x, tocke1[41].y);
var crte16=new Ppoint_list(2, crte16_t);
ppolyline(crte16);

pset_line_colr_ind(4);

var lok_t=new Array();
for (var i=0; i<lokst; i++)
{
lok_t[i]=new Ppoint(lok1[i].x, lok1[i].y);
}
var lok_1=new Ppoint_list(lokst, lok_t);
ppolyline(lok_1);

var lokd_t=new Array();
for (var i=0; i<lokst_d; i++)
{
lokd_t[i]=new Ppoint(lok_d1[i].x, lok_d1[i].y);
}
var lokd1=new Ppoint_list(lokst_d, lokd_t);
ppolyline(lokd1);

var loklz_t=new Array();
for (var i=0; i<lokst_lz; i++)
{
loklz_t[i]=new Ppoint(lok_lz1[i].x, lok_lz1[i].y);
}
var loklz1=new Ppoint_list(lokst_lz, loklz_t);
ppolyline(loklz1);

var lokdz_t=new Array();
for (var i=0; i<lokst_dz; i++)
{
lokdz_t[i]=new Ppoint(lok_dz1[i].x, lok_dz1[i].y);
}
var lokdz1=new Ppoint_list(lokst_dz, lokdz_t);
ppolyline(lokdz1);

// MnogoKot(sx+t[1]/2,sy+(t[3]+t[4]),t[2],36);
//Radij(skrogx,skrogy,t[2],2,224,92);
//Radij(skrogx-t[1],skrogy-((t[3]+t[4])+(t[3]+t[4])),t[2],2,0,90);

//Radij(skrogx,skrogy,t[2],2,224,92);

}

// Izris ležaja

function naris(kaj,id,kot,ska,trax,tray)
{

var postaja = 1;
var povezava = document.Phigs;
var tip = PWODSX;
var Lezaj = 1;

popen_phigs("stderr", 0);
popen_ws(postaja, povezava, tip);
popen_struct(Lezaj);

koordinate();

if (kaj=="0") Izracun(id); else
{
if (izr==0) Izracun(id);
Transformacija(kot,parseFloat(ska,10),parseFloat(trax,10),parseFloat(tray,10));
}
Risi();
pclose_struct();
ppost_struct(postaja, Lezaj, 1.0);
pclose_ws(postaja);
pclose_phigs();
}

</script>
</TD>
</TR>
</TABLE><CENTER>
</body>
</html>

Avtor:
Igor vidmar