1 KAJ JE RAČUNSKA GEOMETRIJA

Splošno gledano je računska geometrija proučevanje algoritmov, s pomočjo katerih se rešujejo geometrijski problemi na računalniku.

Pri ožjem pojmovanju računske geometrije je ta opredeljena kot proces iskanja in razvrščanja preko določene množice elementov. Najpreprostejši primer je razvrščanje po koordinatah. Naj bo niz N sestavljen iz n elementov na realni osi R. Naloga je razvrstiti elemente po njihovih koordinatah. Temu ustreza (Slika 1.1).

Problem razvrščanja: Potrebno je poiskati razvrstitev H(N) na R, ki bo oblikovana iz danega niza točk N.

S problemom razvrščanja se povezuje problem iskanja.

Problem iskanja: Potrebno je združiti razvrstitev H'(N) s H(N) tako, da je pri katerikoli dani točki qR mogoče določiti interval v H(N), ki to točko vsebuje. Iskanje je izvedeno v logaritmičnem času.

Pri dinamičnih procesih se niz N spreminja z dodajanjem oziroma odvzemanjem točk. Tu je potrebno hitro prilagajanje razvrstitev H(N) in H'(N), v logaritmičnem času, med vsako akcijo dodajanja in odvzemanja.

Problema razvrščanja in iskanja se lahko združita: dan je niz N, sestavljen iz n elementov na realni osi R. Oblikovati je mogoče razvrstitvi H(N) in H'(N). S pomočjo slednje je mogoče določiti položaj katerekoli točke v razvrstitvi H(N).

Razvrščanje točk na osi R je najpreprostejši primer računske geometrije. Pri premiku v višje dimenzije, niz elementov N ni več sestavljen iz točk, temveč iz linijskih segmentov, ploskev, polprostorov, itd., v Rd prostoru.

Rd predstavlja d-dimenzijski prostor. Razvrstitev H(N) tako predstavlja razvrstitev vsega ali samo del prostora Rd, sestavljenega iz niza N. H(N) se imenuje tudi geometrijski kompleks. Pod tem se razume zbir razčlenjenih nizov, različnih dimenzij, skupaj z medsebojnimi povezavami v prostoru Rd. Najpreprostejši primer je planarni graf, ki je sestavljen iz temen, robov in ploskev ter povezav med njimi. Element, v geometrijskem kompleksu, dimenzije j se imenuje j-ploskev. 0-ploskev ali ničdimenzijska ploskev je teme, 1-ploskev ali enodimenzijska ploskev je rob, itd. V tem primeru je terminologija prilagojena planarnemu grafu.

1.1 Determinističen in naključen pristop

Reševanja geometrijskih problemov se je mogoče lotiti s pomočjo determinističnih algoritmov ali s pomočjo naključnih algoritmov.

Deterministični načini:

- Inkrementalna meteoda: Dodajanje elementov določenega niza enega za drugim, po znanem vrstnem redu.

- Deljenje in združevanje: Delitev niza po nekem določenem načinu in ponovna združitev.

- Iskanje med zaporednimi razvrstitvami, ki so določene.

- Pregledovanje.

Naključni načini:

- Slučajna inkrementalna metoda: Dodajanje elementov določenega niza enega za drugim brez znanega vrstnega reda.

- Naključno deljenje in združevanje: Naključna delitev niza in ponovna združitev.

- Iskanje med zaporednimi razvrstitvami, ki so naključne.

Slabost determinističnih načinov je v tem, da so težko prilagodljivi razmeram v višjedimenzijskih prostorih. Celo v dvodimenzijskem prostoru so lahko naključni algoritmi učinkovitejši kot deterministični.

1.2 Obravnavane teme

1.2.1 Mnogokotniki

Mnogokotniki so območja na ravnini, ki so od okolice razmejeni z nizom linijskih elementov. Linijski elementi ali robovi se med seboj dotikajo v temenih. Temena so lahko vbočena ali izbočena, kar vpliva na obliko mnogokotnika in na možnost postavitve diagonale med dve temeni. S postavljanjem diagonal v mnogokotnik se doseže triangulacija ali razdeljevanje na trikotnike. Mogoči so še drugi načini razdeljevanja mnogokotnikov: na trapeze, na konveksne površinske elemente. Razdeljevanje mnogokotnikov na površinske podelemente je izvedljivo s pomočjo algoritmov. Nekateri so predstavljeni v nadaljevanju: triangulacija z odstranjevanjem ušes, razdeljevanje na trapeze s pregledovanjem ravnine, inkrementalni algoritem razdeljevanja na trapeze.

Na Sliki 1.2 je prikazan mnogokotnik z osemnajstimi temeni, preko katerega je izvedena tringulacija.

1.2.2 Lupine

Lupina je ovoj, ki je ovit okoli niza točk N na ravnini ali v prostoru. Dotika se samo zunanjih točk niza, medtem ko so ostale točke v notranjosti lupine. Pri lupinah je pomembeno, kako so predstavljene. Lahko kot neurejen sklop zunanjih točk, ki so med seboj načeloma povezane, vendar ta povezava ni nakazana. Ali pa kot urejen niz zunanjih točk v nasprotmi smeri urinih kazalcev, ki jih med seboj povezuje lupina.

Pomembno področje v računski geometriji je konstruiranje lupine iz danega niz točk N. V nadaljevanju so predstavljeni deterministični in naključni algoritmi za konstrukcijo lupin v 2D in 3D.

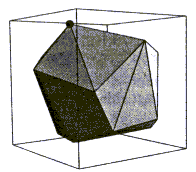
Na Sliki 1.3 je prikazana lupina v 3D, ikozaeder. Sestavljen je iz dvajsetih trikotnikov, ki se med seboj dotikajo v dvanajstih temenih in tridesetih robovih.

1.2.3 Vornoi diagrami

Vornoi diagrami obravnavajo odnose med točkami niza N. Če je niz N setstavljen iz n točk oziroma t.i. leg na ravnini, potem Vornoi diagram ravnino razdeli tako, da v vsakem Vornoi območju leži samo ena lega, rob tega območja pa leži natančno na polovici med dvema sosednjima legama. Lastnosti Vornoi diagramov se uporabljajo pri proučevanju raznih problemov, ki se ukvarjajo z vprašanjem razdalj, raznih optimizacij, itd. Vornoi diagram je tudi osnova za najboljšo možno triangulacijo preko niza točk N. Imenuje se Delaunay-eva triangulacija in je v bistvu dual Vornoi diagrama. Obstajajo še razne posplošitve Vornoi diagramov, kjer lege na ravnini zamenjajo linijski elementi, robovi, itd. Na Sliki 1.4 je prikazan niz dvajsetih točk N na ravnini in Vornoi diagram, ki to ravnino razdeli na Vornoi območja.

1.2.4 Ureditve

Ureditve so na prvi pogled preprosta in trivialna tema. Gre za niz elementov, npr. črt, ki so razporejeni po ravnini ali prostoru. Razporeditev je lahko povsem naključna, brez kakršnihkoli zakonitosti, lahko pa je podrejena natančno določenim zakonom. Ureditve obravnavajo položaj oziroma lego teh elementov na ravnini ali v prostoru. Pri ureditvah je pomembna dualnost, saj je mogoče eno ureditev, npr. črt, prikazati z drugo ureditvijo, npr. točk, ki je dual prve ureditve. Na Sliki 1.5 je prikazana preprosta ureditev desetih črt na ravnini. Te črte ravnino razdelijo na konveksne mnogokotnike, eni so omejeni, drugi ne.

1.2.5 Iskanje točk in presečišč

Algoritmi, ki so predstavljeni v tem poglavju, se ukvarjajo s problemom iskanja točke na ravnini ali v prostoru. Pri prvem primeru gre predvsem za ugotavljanje, ali točka leži v notranjosti mnogokotnika ali zunaj njega in za določanje skrajnih točk konveksnega mnogokotnika. Pri drugem pa za določanje skrajnih točk konveksnega poliedra. Točka kot taka lahko predstavlja tudi presečišče dveh premic, daljic, robov, itd. Pri iskanju preseka dveh konveksnih mnogokotnikov je potrebno poiskati vse točke, ki ležijo na presečiščih robov obeh mnogokotnikov. Ko so vse take točke določene, je mogoče skonstruirati presek dveh konveksnih mnogokotnikov. Na Sliki 1.6 je prikazan polieder in njegova najvišja točka, v tem primeru v smeri koordinatne osi x. Najvišjo točko se lahko določa v katerikoli poljubni smeri u.

1.2.6 Načrtovanje gibanja

Računsko geometrijo je moč uporabiti tudi pri načrtovanju delovnih gibov robotov. Gibanje je potrebno določiti tako, da se roka robota ali ves robot pri svojem delovnem gibu ne zadane ob ovire, ki so postavljene na ravnini ali v prostoru. Model robota je ponavadi mnogokotnik, kadar sta translacija in rotacija samo na ravnini, kadar je gibanje v prostoru, je model robota polieder. Nekonveksni modeli se uporabljajo, kadar je delovni gib zapletena kombinacija translacije in rotacije. Na Sliki 1.7 je prikazana pot robota, ki mora priti od začetne do neke končne točke in se pri tem izogniti dveh ovir, ki sta ponazorjeni z mnogokotnikoma.