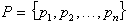 niz točk na ravnini, ki se imenujejo
lege. Vornoi diagram
niz točk na ravnini, ki se imenujejo
lege. Vornoi diagram 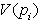 ravnino razdeli
tako, da je
ravnino razdeli
tako, da je 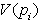 sestavljen iz vseh točk,
ki so vsaj tako blizu legi
sestavljen iz vseh točk,
ki so vsaj tako blizu legi 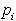 , kot so blizu
katerikoli drugi legi:
, kot so blizu
katerikoli drugi legi:
Drugo najpomembnejše področje v raučunski geometriji
za konveksnimi lupinami so Vornoi diagrami. Obravnavajo sosedske
odnose med točkami niza N: katera točka je kateri najbližja,
katera je od katere najbolj oddaljena, itd.
Naj bo 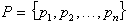 niz točk na ravnini, ki se imenujejo
lege. Vornoi diagram
niz točk na ravnini, ki se imenujejo
lege. Vornoi diagram 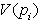 ravnino razdeli
tako, da je
ravnino razdeli
tako, da je 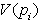 sestavljen iz vseh točk,
ki so vsaj tako blizu legi
sestavljen iz vseh točk,
ki so vsaj tako blizu legi 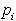 , kot so blizu
katerikoli drugi legi:
, kot so blizu
katerikoli drugi legi:
 .
.
Naj bosta na ravnini samo dve legi, 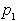 in
in
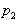 . Naj premica
. Naj premica 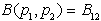 pravokotno razdeli segment
pravokotno razdeli segment 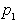
 na dva enaka dela. Potem je vsaka točka x na premici
na dva enaka dela. Potem je vsaka točka x na premici 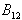 enako oddaljena od lege
enako oddaljena od lege 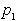 , kakor tudi od
lege
, kakor tudi od
lege 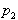 .Velja
.Velja  (Slika
4.1).
(Slika
4.1).

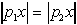 .
.
Če ležijo na ravnini tri lege 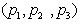 , te definirajo
trikotnik. Razpolovnice stranic trikornika B12, B23
in B31 se sekajo v točki, ki je središče očrtanega kroga
(Slika 4.2). Ta točka ni nujno v notranjosti trikotnika.
, te definirajo
trikotnik. Razpolovnice stranic trikornika B12, B23
in B31 se sekajo v točki, ki je središče očrtanega kroga
(Slika 4.2). Ta točka ni nujno v notranjosti trikotnika.
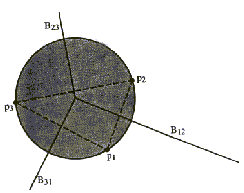
Iz prvih dveh primerov je razvidno, da imajo razpolovnice Bij
pomembno vlogo. Naj bo H(pi,pj) zaprta polravnina,
ki je omejena z Bij in vsebuje točko pi. Potem lahko
H(pi,pj) razumemo kot vse točke, ki so bliže
pi kot pj. Kot že omenjeno je V(pi)
niz točk, ki so bliže legi pi, kot katerikoli drugi legi:
z drugimi besedami, točke bliže pi kot p1, bliže
pi kot p2, bliže pi kot p3, itd. Upoštevaje
navedeno je mogoče napisati enačbo za Vornoi diagram V(pi):
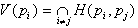 ,
,
pri čemer je potrebno upoštevati presek preko vseh i in j, za katere velja ij. Iz enačbe sledi lastnost Vornoi diagrama: območja Vornoi diagrama so konveksna, ker nastanejo kot presečišča večih polravnin. Kadar so ta območja omejena, so to konveksni mnogokotniki. Robovi se imenujejo Vornoi robovi in temena Vornoi temena. Katerakoli točka na Vornoi robu ima dve najbližji legi, Vornoi teme pa ima najmanj tri najbližje lege.
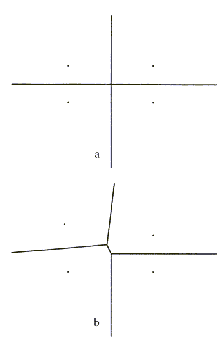
V primeru štirih leg na ravnini, ki oblikujejo vogale kvadrata,
je Vornoi diagram kot je prikazano na Sliki 4.3a. Vornoi teme
je v tem primeru četrte stopnje. Če se eno lego nekoliko premakne
(Slika 4.3b), postane diagram normalen. Prvi primer je izrojen
zaradi centričnega položaja štirih leg.
Vorni diagram z večimi legami bi izgledal kot na Siki 4.4.

Delaunay-eva triangulacija nastane takrat, kadar se med seboj
povežejo lege, ki imajo skupen Vornoi rob. Delaunay-eva triangulacija
D (P)
in Vornoi diagram V(P)
predstavljata dualnost; isti podatki so predstavljeni na dva različna
načina.
Na Sliki 4.4 je prikazan Vornoi diagram z dvajsetimi
legami. Na Sliki 4.5 je prikazana Delaunay-eva triangulacija teh
istih dvajsetih leg. Na Sliki 4.6 sta prikazana Delaunay-eva triangulacija
in Vornoi diagram skupaj.
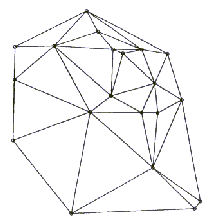
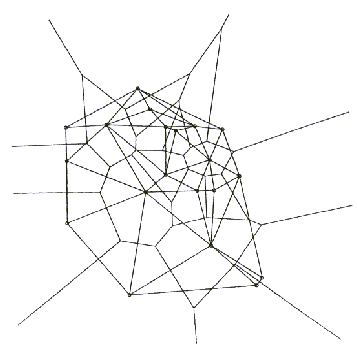
Za razumevanje obeh pomembnih struktur D
(P) in V(P)
je potrebno poznati odnos med njima. Naj bo P nespremenljiv
niz leg. Za Delaunay-evo triangulacijo veljajo lastnosti:
D1. D
(P) je ravnočrtna dualnost V(P),
po definiciji.
D2. D
(P) je triangulacija, če ne obstajajo
štiri centrične lege: vsaka površina je trikotnik. Ploskve
D (P)
so Delaunay-evi trikotniki.
D3. Vsak trikotnik grafa
D (P)
ustreza temenu grafa V(P).
D4. Vsak rob grafa D
(P) ustreza robu grafa V(P).
D5. Vsak vozel grafa D
(P) ustrez območju grafa V(P).
D6. Meja D
(P) je konveksna lupina
D7. Notranjost trikotnikov
D (P)
ne vsebuje nobenih leg.
Za Vornoi diagram veljajo lastnosti:
V1. Vsako Vornoi območej
V(pi) je konveksno.
V2. V(pi)
je neomejeno, če je pi na konveksni lupini niza leg.
V3. Če je Vornoi teme
na stičišču V(p1), V(p2) in V(p3),
potem je v središču kroga C(v), ki ga določajo
p1, p2 in p3.
V4. C(v)
je očrtan krog pri Delaunay-evi triangulaciji, ki ustreza v.
V5. V notranjosti C(v)
ni nobene lege.
V6. Če je pj najbližji
pi, potem je (pj,pi) rob triagulacije D(P).
V7. Če obstaja krog skozi
pi in pj, ki ne vsebuje nobenih drugih leg, potem
je (pi,pj) rob triangulacije D
(P).
Za konstrukcijo Vornoi diagrama obstaja cela vrsta algoritmov.
Leta 1985 je Fortune izdelal algoritem, ki temelji na principu
pregledovanja ravnine. Na prvi pogled je nerazumljivo, kako lahko
nastaja diagram za linijo, če nanj vplivajo lege, ki so pred pregledovalno
linijo in še niso bile pregledane.
Naj bodo lege na xy ravnini del tridimenzijskega koordinatnega
sistema. Nad vsako lego naj bo postavljen stožec z nagibom 45o,
ki ima vrh v legi p. V tretji dimenziji je to vidno kot
čas; stožec nad p predstavlja krog, ki se veča: po času
t ima radij t. Naj imata legi p1 in p2
vsaka svoj stožec. Presečišče teh dveh stožcev je krivulja v prostoru,
njena projekcija pa je ravna črta na xy ravnini (Slika
4.7).
4.3 Konstrukcija Vornoi diagrama
4.3.1 Determinističen algoritem za konstrukcijo Vornoi diagrama

Gledano iz  , bi projekcije vseh krivulj,
ki so presečišča stožcev, predstavljale Vornoi diagram na ravnini
xy. To lastnost je Fortune uporabil pri svoji metodi. Ravnina
se pregleduje s pomočjo ravnine , ki je proti xy nagnjena
za 45o. Pregledovalna črta L je presečišče med ravninama
in xy. Naj bo L paralelna y osi, koordinata
x pa naj bo l (Slika 4.8).
, bi projekcije vseh krivulj,
ki so presečišča stožcev, predstavljale Vornoi diagram na ravnini
xy. To lastnost je Fortune uporabil pri svoji metodi. Ravnina
se pregleduje s pomočjo ravnine , ki je proti xy nagnjena
za 45o. Pregledovalna črta L je presečišče med ravninama
in xy. Naj bo L paralelna y osi, koordinata
x pa naj bo l (Slika 4.8).
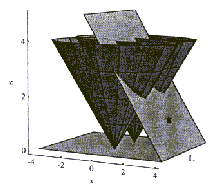
Slika 4.8 Stožca presekana s pregledovalno ravnino. Ravnina
in linija L se pomikata v desno.
Na strani xl črte L je od spodaj vidna samo ravnina
. Ta zakriva del stožcev, obenem pa predstavlja del ravnine, ki
jo je potrebno še pregledati. Na strani xl črte L,
je viden Vornoi diagram vse do presečišča ravnine s stožcema.
Presečišče ravnine s stožcem je parabola, tako je tudi presečišče
ravanine z desno stranjo stožcev parabola. Ta se na ravnino xy
(gledano iz  ) projecira kot parabolično
čelo, ki je sestavljeno iz večih elementarnih parabol (Slika 4.9).
) projecira kot parabolično
čelo, ki je sestavljeno iz večih elementarnih parabol (Slika 4.9).

 .
Odebljena črta je parabolično čelo.
.
Odebljena črta je parabolično čelo.
Dve paraboli se stikata v točki, kjer se ravnina dotika obeh
stožcev. Iz prej navedenih ugotovitev je na tem mestu Vornoi rob.
Ker je pregledovalna ravnina nagnjena pod istim kotom kot stranica
stožca, sreča L lego p v trenutku, ko pregledovalna ravnina
zadane ob stožec lege p. Tako Vornoi diagram ne nastaja
samo levo od pregledovalne črte L, ampak ves čas tudi pod
ravnino . Torej, Vornoi diagram nastaja levo od pregledovalne
črte L, navzgor do paraboličnega čela, ki za L nekoliko
zaostaja.
Inkrementalni algoritem za konstrukcijo Vornoi diagrama temelji
na postopnem dodajanju leg po naključnem vrstnem redu; podobno
kot že opisani inkrementalni algoritmi. Naj bo N niz leg
na ravnini in G(N) Vornoi diagram, ki ga te lege
določajo. Naj bo Ni niz prvih i naključno izbranih
leg. Na vsaki stopnji i algoritem določi Vornoi diagram
G(Ni). Diagram G(Ni+1) nastane iz
G(N) kot je prikazano na Sliki 4.10.
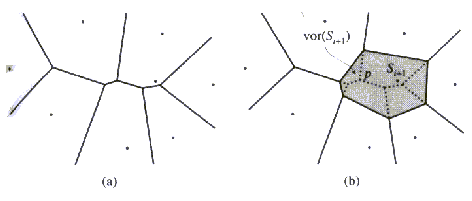
Naj bo SSi+1 i+1 lega, ki je dodana naključno. Najprej
je potrebno poiskati točko p v G(Ni), ki
leži v Vornoi območju točke S. V tem primeru je S
bližja točki p kot katerikoli drugi sosednji legi v G(Ni).
Jasno je, da v diagramu G(Ni+1) točka p ne
bo več njegov del. V vsakem trenutku dodajanja i+1 je možnih
več točk p, vendar zadostuje ena sama, ki je izbrana naključno.
Ostale točke (temena Vornoi diagrama), ki so v območju S,
je moč poiskati v diagramu G(Ni). Iskanje se začne
v točki p in je preprosto izvedljivo, saj so sosednja temena
med seboj povezana z Vornoi robovi. Robovi, ki so temenom p
sosednji, se skrajšajo ali odstranijo. Če ima Vornoi rob obe krajišči
v točkah p, se odstrani, če je točka p samo eno
krajišče, se rob skrajša. Na koncu je potrebno določiti še robove
Vornoi območja dodane lege S. Ti robovi povezujejo med
seboj krajišča odrezanih robov v krožnem vrstnem redu. Mesta,
kjer se robovi odrežejo, so določljiva z razpolavljanjem povezav
med lego S in ostalimi sosednjimi legami. Tako dobljen
diagram je G(Ni+1).
S konstrukcijo Vornoi diagrama je povezanih več aplikacij: najbližji
sosed, maksimiziranje najmanjših kotov pri triangulaciji, največji
prazen krog, najmanjše razvejišče, problem trgovskega potnika,
itd.
Problem najbližjega soseda je iskalne narave. Potrebno je poiskati najbližjega soseda določeni točki oziroma poiskati najbližjega soseda vsaki izmed točk niza P. S tem problemom se ukvarjajo na različnih področjih: biologija, ekoligija, geografija, fizika, itd.
Definicija problema:
b je najbližji sosed a-ja, če  ,
pri čemer je cP. Lahko se tudi zapiše ab ali najbližji
sosed a-ja je b. Ta trditev ni simetrična, saj ni
nujno, da hkrati velja tudi ba (Slika 4.11).
,
pri čemer je cP. Lahko se tudi zapiše ab ali najbližji
sosed a-ja je b. Ta trditev ni simetrična, saj ni
nujno, da hkrati velja tudi ba (Slika 4.11).
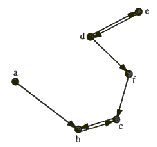
Naj bo P niz točk, preko katerega se lahko določi Vornoi
diagram. Pri iskanju najbližjega soseda točki q se problem
zreducira na iskanje Vornoi območja, v katerem ta točka leži.
Vse lege v tem območju so najbližji sosedi točki q.
Pri analiziranju kompleksnejših oblik se uporabljajo metode končnih elementov. Tako npr. pri načrtovanju avtomobilskih lupin. Stabilnost numeričnega postopka je odvisna od kvalitete razdelitve. Iskaže se, da Delaunay-eva triangulacija spada med dobre razdelitve.
Naj bo S niz točk, preko katerih je izvedena triangulacija.
Linijski segmenti se med seboj sekajo (v svojih krajiščih) samo
v točkah niza S. Konveksna lupina je razdeljena na trikotnike.
Z vidika končnih elementov je dobra tista razdelitev, ki uporablja
debele trikotnike. Izogniti se je potrebno trikotnikom z majhnimi
koti. Iz tega sledi postopek maksimiziranja najmanjših kotov.
Natančen odgovor na to je Delaunay-eva triangulacija. Naj bo T
triangulacija niza S, naj bo zapis kotov te triangulacije
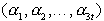 , razvrščenih od najmanjšega do največjega,
pri čemer je t število trikotnikov v T. Število
T je konstantno za vsak niz S. Med dvema triangulacijama
istega niza S je določljivo razmerje
, razvrščenih od najmanjšega do največjega,
pri čemer je t število trikotnikov v T. Število
T je konstantno za vsak niz S. Med dvema triangulacijama
istega niza S je določljivo razmerje 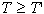 glede na njuno debelost, če velja: 11' ali 11' in 22' ali 11',
22' in 33 itd. Iz vsega sledi, da je Delaunay-eva triangulacija
T=D(P)
največja glede na velikost kotov v odnosu
glede na njuno debelost, če velja: 11' ali 11' in 22' ali 11',
22' in 33 itd. Iz vsega sledi, da je Delaunay-eva triangulacija
T=D(P)
največja glede na velikost kotov v odnosu 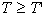 glede na katerokoli razdelitev T' preko niza točk P.
glede na katerokoli razdelitev T' preko niza točk P.
Potrebno je poiskati največji prazen krog, čigar center je v notranjosti konveksne lupine, ki jo določa niz točk S. Prazen v tem smislu, da v njegovi notranjosti ne leži nobena točka niza S in največji, da ne obstaja noben tak krog, ki bi imel nedvoumno večji radij. V praksi je to primerljivo z iskanjem lokacije za postavitev jedrskega reaktorja, ki naj bo zgrajen čim dalj od naseljenih krajev. Naj bo f(p) polmer največjega praznega kroga s centrom v točki p. Poiskati je potrebno maksimum te funkcije preko vseh p-jev v konveksni lupini S, H=H(S). Navidezno obstaja neskončno možnosti za točko ekstrema. Izkaže pa se, da je takih točk končno mnogo.
Naj bo nekje v notranjosti H prazen krog s
središčem v točki p, ki mu povečujemo polmer. V nekem trenutku
bo ta krog zadel ob eno izmed leg  in
imel pri tem vrednost f(p). Če krog zadane samo
ob eno lego, npr. s1, potem je jasno, da f(p)
ni maksimum. Če se p po premici s1p pomakne
stran od s1 v točko p', potem je f(p')f(p)
(Slika 4.12).
in
imel pri tem vrednost f(p). Če krog zadane samo
ob eno lego, npr. s1, potem je jasno, da f(p)
ni maksimum. Če se p po premici s1p pomakne
stran od s1 v točko p', potem je f(p')f(p)
(Slika 4.12).

Recimo, da pri razdalji f(p) krog zadane
on natančno dve legi s1 in s2. Tudi v tem primeru
f(p) ne more biti maksimum. Točko p je mogoče
po razpolovnici s1s2 pomakniti stran od s1
in s2 v točko p'. Potem velja f(p')f(p)
Slika 4.12). Iz tega sledi, da funkcija f(p) doseže
maksimum samo v primeru, če krog v trenutku zadane ob najmanj
tri lege hkrati. Vsako premikanje p bi v tem primeru pomenilo
približevanje h neki legi in s tem manjšanje f(p).
Če je torej center p največjega praznega kroga v notranjosti
lupine H(S), potem mora p sovpadati z Vornoi
temenom. Če p leži na lupini H(S), potem
mora p ležati na Vornoi robu. S tem je določenih končno
število možnih točk. Med vsemi je potrebno poiskati tisto, ki
ima f(p)max.
Algoritem: Največji prazni krog Preračunaj Vornoi diagram V(S) preko S. Preračunaj konveksno lupino H. for za vsako Vornoi teme n do if v v notranjosti H: vH then Izračunaj radij kroga s centrom v v in vnesi max. for za vsak Vornoi rob e do Izračunaj peH presečišče med e in mejo lupine. Izračunaj radij kroga s centrom v p in vnesi max. Vrni max. |
Najmanjše razvejišče je problem, pri katerem je potrebno točke
niza S povezati med seboj tako, da bo imela nastala drevesna
struktura najmanjšo mogočo dolžino. V praksi je to primerljivo
z načrtovanjem lokalnih mrež, kjer je potrebno s kablom povezati
med seboj uporabnike na različnih lokacijah. Ideja algoritma je,
da je potrebno med seboj združiti vse majkrajše robove e,
ki povezujejo med seboj vse točke niza G.
Problem trgovskega potnika je eden bolj proučevanih v računski
geometriji. Je povsem praktične narave in ga je moč uporabiti
pri številnih primerih. Glavno vprašanje je, po kateri poti naj
hodi trgovski potnik, da bo obiskal vsa mesta in, da bo pot najkrajša
možna. Ali, kako z neprekinjeno črto povezati med seboj vse točke
niza M tako, da bo ta črta najkrajša mogoča.
Lastnosti Vornoi diagrama omogočajo posplošitve v večih smereh,
kar se izkaže kot zelo uporabno na različnih praktičnih področjih.
Vornoi diagram je v svoji osnovi določen kot sklop točk, za katere
velja, da ima vsaka najmanj dve najbližji legi iz niza točk P.
Ena izmed posplošitev je sistem srednjih osi. Srednje osi so skup
točk v notranjosti P, ki imajo najmanj dve najbližji točki
na meji P mnogokotnika P. V tem primeru prej omenjene
lege zamenja meja mnogokotnika P. Srednje osi pravokotnika
so prikazane na Sliki 4.13. Vsaka točka horizontalnega segmenta
v kvadratu je enako oddaljena od zgornjega in spodnjega roba mnogokotnika
P. Vsaka točka na diagonalnem segmentu je enako oddaljena
od točk na sosednjih robovih mnogokotnika P. Bolj kompleksen
primer je prikazan na Sliki 4.14. Srednje osi imajo drevesno strukturo.
Vsaka točka na srednjih oseh je središče kroga, ki se meje mnogokotnika
P dotika v najmanj dveh točkah. Krog, s središčem v stičišču
srednjih osi, se meje mnogokotnika P dotika v treh točkah
(Slika 4.15).
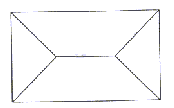
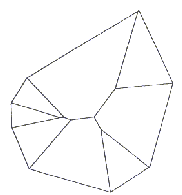

Slika 4.15 Krog s središčem v stičišču srednjih osi se
dotika meje mnogokotnika P v treh točkah.