5 UREDITVE

Za konveksnimi lupinami in Vornoi diagrami zavzemajo pomembno mesto v računski geometriji ureditve. Naj bo N niz elementov v Rd. Ureditev H(N), sestavljena iz elementov niza N je naravna razdelitev Rd na več konveksnih območij različnih dimenzij. Na Sliki 5.1 je prikazana ureditev črt na ravnini. Te črte razdelijo ravnino na konveksna področja, linijske segmente med presečišči in temena, kjer se črte sekajo. Na ureditve je primerno gledati kot na zbir nepovezanih elementov. Območja so odprta, brez robov. Linijski segmenti so odprti, brez krajnih temen. Vsi skupaj sestavljajo ureditev.

Ureditev črt je preprosta, če se vsak par črt seka v natančno eni točki. To pomeni, da se v eni točki ne morejo sekati tri črte in, da niti dve črti nista vzporedni. Nepreproste ureditve so tako na nek način deformirane. Za nepreproste ureditve so teoremi in algoritmi precej bolj zapleteni kot za preproste. Za preproste ureditve z n črtami celo valja, da imajo vse natanko enako število temen, robov in področij. Preprosta ureditev z n črtami ima temen, E=n2 robov in področij. Na Sliki 5.1 je preprosta ureditev, na Sliki 5.2 pa nepreprosta.

Kljub navidezni trivialnosti so ureditve v praksi obravnavano območje. Primer je odstranjevanje nevidnih površin. Gre za predelavo 3D prostora v dvodimenzijsko grafično podobo, kakršna bi bila videna iz določene točke gledanja. Naslednji je problem iskanja največje prazne konveksne lupine, ki jo lahko skonstruiramo iz niza točk N. Največje v smislu z največ temeni. Potem razdeljeanje niza točk N na dva enakovredna dela, itd.

5.1 Inkrementalni algoritem

Najučikovitejši in hkrati najpreprostejši algoritem za konstruiranje črtne ureditve je inkrementalni algoritem. V vsakem trenutku je podana ureditev A i-1, ki je določena iz i-1 črt. potrebno je poiskati presečišča med A i-1 in i-to dodano črto Li. Najprej je potrebno poiskati katerokoli točko, ki je presečišče med Li in katerokoli črto podane ureditve A i-1. Na Sliki 5.3 je taka točka x=LiL2. V naslednjem koraku je potrebno pregledati vsako območje okoli Li, Z(Li). To se naredi tako, da se območja okoli Li pregleduje po njihovih robovih v smeri urinih kazalcev, dokler se ne ugotovi presečišč med Li in A i-1.

Na Sliki 5.3 je prikazan opisani način iskanja. Začetek je v točki x. Pregleduje se območje C oziroma njegove robove v smeri urinih kazalcev, dokler ni odkrito novo presečišče z Li. V tem primeru presečišče med L3 in Li. Pregledovanje se nadaljuje naprej v območjih D, E dokler ni odkrito tako območje, ki ima z Li samo eno presečišče. Nato se pregleda še območja, ki so levo od točke x. Tu se robovi pregledujejo v nasprotni smeri urinih kazalcev. Princip je identičen. Vsa ugotovljena presečišča se na koncu pregledovanja, ali še bolje sproti, vpisujejo v A i-1. Stara ureditev A i-1 je preurejena v novo A i. Sledi dodajanje naslednje črte.

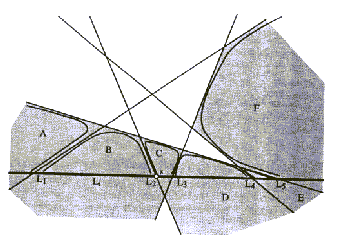
Slika 5.3 Dodajanje črte Li v ureditev. Označene so poti pregledovanja oziroma iskanja presečišč.

5.2 Dualnost

Vzporedno z ureditvijo črt je mogoče obravnavati tudi ureditve točk. Pri tem gra za dualnost. Kot že omenjeno, gre za podatke, ki jih je mogoče predstaviti na dva različna načina. Črte, za katerih zapis sta potrebna dva podatka, se lahko poveže s točkami, za katerih zapis sta prav tako potrebna dva podatka. Črta, ki je določena z y=mx+b, je lahko prikazana s točko (m,b). Ko je določena preslikava iz črte v točko je hkrati določena tudi nasprotna preslikava. Vsako točko je mogoče razumeti kot črto, ki je določena z dvema podatkoma. Naklonom in presečiščem. Obe preslikavi, iz črte v točko in iz točke v črto, skupaj določata dualnost: vsaka črta je povezana z neko točko in vsaka točka je povezana z nako črto. Med točko in črto je možnih več različnih dualnosti, kar je odvisno predvsem od načina predstavitve črte. Vsaka od preslikav ima svoje prednosti in slabosti, zato je za posamezne primere potrebno izbrati primerne preslikave. Preslikave so:

1. že omenjena ,

2. preslikava 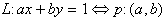znana pod imenom polarna dualnost,

3. preslikava 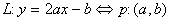, ki je zaradi svojih lastnosti posebej primerna za računsko geometrijo, itd.

Naj bo D oznaka za dualnost, potem velja D(L)=p in D(p)=L. Povezava med točko p=(a,b) in črto je na prvi pogled nenavadna. Izkaže se, da L nakaže povezavo s parabolo y=x2. Ta parabola ima v točki (a,a2) tangento y=2ax-a2. Preslikava D(p) točko p=(a,b) z b=a2 preslika ravno v to tangento (Slika 5.4). To je ena glavnih lastnosti, zakaj je ta preslikava zanimiva za računsko geometrijo.

Slika 5.4 D(a)=A, D(b)=B, D(c)=B.

Glavne lastnosti dualnosti so:

1. Preslikava D je sama sebi nasprotna D(D(x))=x, kjer je x ali črta ali točka.

2. D poveže eno-z-eno vse nevertikalne črte in vse točke na ravnini.

3. Točka p leži na črti L, če točka D(L) leži na črti D(p).

4. Črti L1 in L2 se sekata v točki p, če črta D(p) teče skozi dve točki D(L1) in D(L2).

5. Če točka p leži nad črto L, potem leži črta D(p) pod točko D(L) in obratno, če p leži pod črto L, leži črta D(p) nad točko D(L).

Na Sliki 5.5 je prikazana dualnost med črtami in točkami. Vsaka izmed desetih črt ima svojo točko in obratno.

Slika 5.5 Dualnost črt in točk.

5.3 Odstranjevanje nevidnih površin

Glede na vse večjo prisotnost posebnih efektov v filmski industriji, se računska geometrija ukvarja s problemom odstranjevanja nevidnih površin. Iz niza prozornih poliedrov v 3D prostoru je potrebno določiti postavitev v 2D prostoru, kakršna bi bila vidna iz določene točke gledanja. Ker se v prvotnem stanju površine posameznih lupin prekrivajo, je potrebno prekrite oziroma nevidne površine v drugi fazi odstraniti. Od tod ime odstranjevanje nevidnih površin.

Za uspešno izvajanje algoritma je potrebno privzeti dve predpostavki. Poliedri v prostoru naj ne prebadajo drug drugega oziroma, njihove notranjosti naj bodo ločene. Skupne imajo lahko samo mejne točke. In druga, točka gledanja naj bo postavljena v neskončnost (0,0,+). S tem so odpravljene težave zaradi perspektive. Projekcijska ravnina naj bo xy, z=0. Izkaže se, da prestavljanje točke gledanja iz neskončnosti v nek drug položaj ni nepremostljivo.

Pod vse poliedre je primerno postaviti osnovni mnogokotnik oziroma podlago, ki uokviri vse elemente, ki jih je potrebno obdelati.

V prvem koraku je potrebno vse robove poliedrov projecirati na ravnino xy. To se naredi tako, da se temenom teh robov odpiše koordinata z. Rezultat tega je ureditev A , sestavljena iz n črt na ravnini xy. V naslednjem koraku potrbno za vsako področje ureditve A določiti, kateri mnogokotnik je v prostoru višji oziroma bližji točki gledanja. To se naredi s pomočjo vertikalne pregledovalne črte, ki se pomika preko ureditve A . Za razkiko od že omenjenega pregledovanja ravnine, v tem primeru pregledovalna črta ni ravna, temveč upogljiva. Preko A je upognjena tako, da vsako črto ureditve A seka natančno enkrat. S tem je prihranjen čas, ki je potreben za iskanje naslednjega temena. Vsa področja, ki jih pregledovalna črta L v določenem trenutku seka, so aktivna področja. Za vsak trenutek mora obstajati seznam aktivnih področij in seznam mnogokotnikov, ki se projecirajo v ta aktivna področja. Ti mnogokotniki so urejeni po koordinati z. Seznam aktivnih celic vsebuje dovolj informacij, da se da določiti mnogokotnik, ki je najbližji točki gledanja. Ko pregledovalna črta L preide teme, staro aktivno območje ugasne, področje desno od temena postane novo aktivno področje. Po pregledovanju ostanejo mnogokotniki, ki imajo največjo vrednost koordinate z, kar je projekcija stanja v prostoru na ravnino.

Slika 5.6 Področje C je aktivno.

Na Sliki 5.6 je prikazana upogljiva pregledovalna črta L in aktivno območje C. Ko bo črta L prešla teme v, bo področje C ugasnilo, aktivno bo postalo sosednje.

Na Sliki 5.7 je prikazano začetno in končno stanje odstranjevanja nevidnih površin.

Slika 5.7 Odstranjevanje nevidnih površin.