V nadaljevanju je predstavljenih nekaj problemov,
ki se ukvarjajo z odkrivanjem točk in presečišč na ravnini ali
v prostoru.
Najbolj preprost primer je določanje točke v mnogokotniku. Naj
bo P mnogokotnik na ravnini in q poljubna točka
te ravnine. Vprašanje je, ali točka q leži v notranjosti
mnogokotnika P oziroma na njegovi meji P, ali zunanj
mnogokotnika P. Če je P konveksen mnogokotnik, potem
je problem rešljiv z že omenjeno predpostavko levega. Pri nekonveksnem
mnogokotniku ta način odpove. V tem primeru se uporabljata dve
metodi: štetje presečišč in metoda zavojnega števila.
Pri prvi metodi je potrebno iz točke q potegniti premico,
recimo v smeri +x. Potrebno je prešteti vsa presečišča
med premico r in mejo mnogokotnika P. Če je število
presečišč sodo število, je točka q zunaj mnogokotnika P,
če je število presečišč liho število, je točka q v notranjosti
mnogokotnika P. Če se pomikamo po premici r iz +
proti točki q, je prvo presečišče vstop v mnogokotnik P,
drugo je izstop iz mnogokotnika P, tretje spet vstop v
mnogokotnik, itd. Kljub preprostosti je algoritem občutljiv na
posebne primere, ko premica r sovpada z robom P,
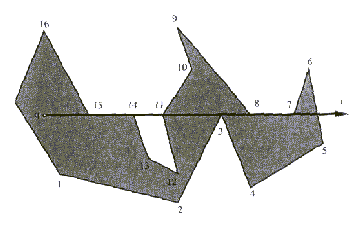
ali ko premica r zadane v teme mnogokotnika P (Slika
6.1).

Rešitev je omejitev, ki določa, kdaj se rob e upošteva
kot presečišče in kdaj ne. Da je rob e presečišče, mora
biti eno teme nedvnoumno nad premico r, drugo pa mora biti
nedvoumno pod ali natančno na premici r. Tako na Sliki
6.1 robovi (7,8), (11,12), (13,14) in (14,15) niso upoštevani
kot robovi, pri katerih premica r preide iz zunanjosti
v notranjost mnogokotnika in obratno. Med posebnimi robovi se
upoštevajo le (6,7), (8,9), (10,11) in (15,16).
Druga metoda se imenuje metoda zavojnega števila in je zastavljena
na povsem drugačen način kot prva. Naj namišljeni gledalec stoji
v točki q, za katero je potrebno ugotoviti ali je v notranjosti
ali zunaj mnogokotnika P. Po meji mnogokotnika naj potuje
točka p v nasprotni smeri urinih kazalcev. Gledalec v točki
q naj se ves čas obrača tako, da bo s pogledom obrnjen
proti točki p. Če je qP, potem je gledalec pri opazovanju
točke p naredi poln obrat 2 rad. Če je qP, potem
je gledalec naredi skupni kot 0rad. Za obrat velja vsota
vseh obratov in sicer, če se gledalec obrača v nasprotni smeri
urinih kazalcev, se kot veča in obratno. Pri konveksnih mnogokotnikih
je uspešnost metode očitna, izkaže pa se, da je uspešna tudi pri
nekonveksnih mnogokotnikih (Slika 6.2).
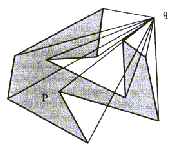
Pogosto je potrebno pri konveksnih mnogokotnikih poiskati skrajne točke v določenih smereh. Tak primer je, kadar želimo poiskati najmanjšo škatlo, v katero je mogoče spraviti konveksni mnogokotnik. V tem primeru je potrebno poiskati štiri skrajne točke.
Potrebno je poiskati skrajno točko konveksnega mnogokotnika. Naj bo to točka z največjo vrednostjo y. Naj ima mnogokotnik P n temen P0,...,Pn-1. Predpostavimo, da lahko v nekem trenutku iskanja zagotovo trdimo, da je najvišje teme v nasprotni smeri urinih kazalcev med indeksoma a in b. Če je ab, potem je eno izmed razpoložljivih temen Pa, Pa+1,...,Pb-1,Pb najvišje teme mnogokotnika. Naj bo c indeks temena, ki nedvoumno leži med temenoma a in b. Predpostavimo, da je rob A za temenom Pa usmerjen navzgor. Če je rob C, ki leži za temenom Pc, tudi usmerjen navzgor (Slika 6.3), potem se interval a,b skrajša na c,b ali na a,c, v odvisnosti ali je Pc višje ali nižje od Pa.
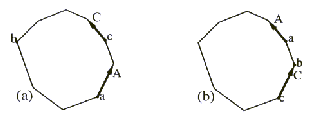
Podobno skrajšanje intervala se naredi, če je rob A obrnjen
navzdol. Postopek se ponavlja toliko časa, dokler ni rob za temenom
c obrnjen navzdol in rob pred temenom c obrnjen
navzgor.
Pomembno področje v računski geometriji je tudi iskanje presečišča med dvema konveksnima mnogokotnikoma. Ideja naslednjega algoritma je preprosta. Naj bosta meji mnogokotnikov P in Q P in Q orientirani v nasprotni smeri urinih kazalcev. Naj bosta A in B trenutno opazovana robova na teh mejah. Algoritem opazuje robova A in B, ki se pomikata v nasprotni smeri urinih kazalcev in uravnava njuni hitrosti tako, da je vsako presečišče med P in Q, oziroma med A in B, določljivo.
Na Sliki 6.4 je prikazan postopek pomikanja obeh aktivnih robov
A in B v nasprotni smeri urinih kazalcev.

Prvi problem predstavlja pomikanje obeh aktivnih robov A
in B vzdolž obeh mej P in Q mnogokotnikov
P in Q. Naj bo a vrh robova A in b
vrh robova B. Če se B pomakne proti robu A,
vendar ga ne doseže, je potrebno ponovno pomakniti rob B
proti verjetnemu presečišču z robom A. Situacija je enaka,
kot je prikazano na Sliki 6.5.

Naj bo H(A) zaprta polravnina (mnogokotnik) na levi
strani roba A. Za določanje aktivnega roba, ki ga je potrebno
pomakniti naprej, je primerna uporaba vektorskega produkta:
če A X B 0 in b H(A), ali
če A X B 0 in b H(A),
potem se naprej pomakne B.
Če A X B 0 in a H(B), ali
Če A X B 0 in a H(B),
potem se naprej pomakne A.
Vse možne kombinacije so prikazane v Tabeli 6.1.
Tabela 6.1
Vsa tako določena presečišča so temena novega mnogokotnika,
t.j. preseka med dvema konveksnima mnogokotnikoma. Robovi novega
mnogokotnika so notranji robovi med A in B, ki povezujejo
med seboj nova temena.
Med enodimenzijskim iskanjem po meji mnogokotnika P in dvodimenzijskim iskanjem po ploskvi poliedra P ni nobenih neposrednih povezav. V drugem primeru dvodimenzionalnost dopušča veliko več svobode, kar precej otežuje iskanje v primerjavi s prvim primerom. Ideja algoritma temelji na razbitju osnovnega poliedra na več poliedrov po hierarhičnem vrstnem redu. Tako se pride s postopnim prehajanjem iz notranjega, najmanjšega poliedra Pk, do osnovnega, največjega poliedra P. P = P0,P1,P2,...,Pk.
Naj bo Pk notranji polieder in ai skrajna točka
poliedra Pi. Najprej je potrebno poiskati skrajno točko
ak poliedra Pk. To je preprosto, saj ima Pk
le tri ali štiri temena. Ko je ak poznan, se zmanjša število
možnih mejnih točk pri Pk-1. Mejno teme na tej stopnji
je ak-1, to pripelje naprej do ak-2, itd. Za razumevanje
povedanega, je potrebno najprej obdelati nekaj osnovnih idej.
Na sliki 6.6 je prikazan planarni graf ikozaedra (ikozaeder na
Sliki 6.7). To je način prikazovanja tridimenzionalnih teles na
ravnini.
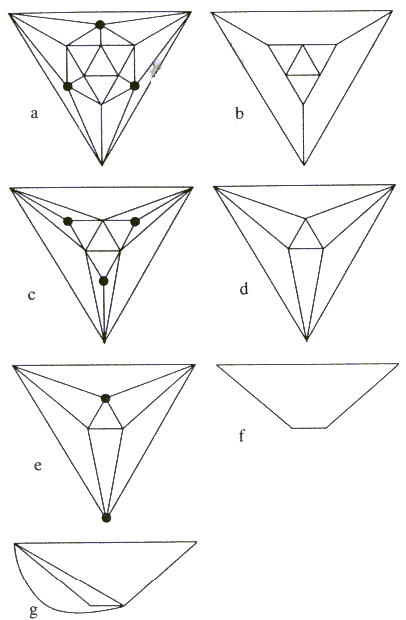
Slika 6.6 Planarni graf, ki prikazuje temena in robove
ikozaedra. Temno označena temena predstavljajo neodvisen niz.
(a) oroginalni graf P0; (b) po brisanju neodvisnega niza;
(c) po ponovni triangulaciji, P1; (d) po brisanju; (e)
po ponovni triangulaciji P2;(f) po brisanju,P3.
Do notranjega poliedra Pk se pride postopoma z odstranjevanjem
neodvisnih nizov. Niz vozlišč I grafa G je imenovan
neodvisen niz, če nobena dva vozlišča v I nista sosednja
v grafu G. V nekem smislu so vozlišča neodvisnega niza
v G razpršena. Tak neodvisen niz je prikazan na Sliki 6.6a.
To je niz treh vozlišč, ki predstavlja največji neodvisni niz
za ta graf, v smislu, da ne obstaja nobena kombinacija štirih
vozlišč, ki bi oblikovala neodvisen niz. Prvi največji polieder
v P je P0 (Slika 6.7).
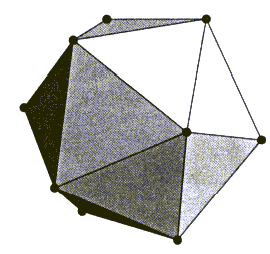
V P0 je potrebno poiskati neodvisen niz (Slika 6.6a). Ta
temena in robove, ki se jih dotikajo, je potrebno zbrisati. Rezultat
je prikazan na Sliki 6.6b. Ker so robovi, ki pripadajo neodvisnim
temenom, prav tako neodvisni, njihov zbris povzroči nastanek novih
ploskev. Naslednji korak je triangulacija novega stanja (Slika
6.6c). Nastane nov polieder P1, ki je nedvoumno manjši,
in je v notranjosti poliedra P0. Na Sliki 6.8 je prikazan
polieder P1.
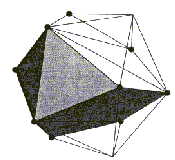
Za konstrukcijo poliedra P2 je potrebno postopek ponoviti.
Neodvisni niz poliedra P1 je določen kot je prikazano na
Sliki 6.6c. Pripadajoča temena in robovi se zbrišejo. Ker je tako
nastali graf sestavljen iz samih trikotnikov, nadaljna triangulacija
ni mogoča; ni potrebna (Slika 6.6d). Sliki 6.6d ustreza oktaeder
na Sliki 6.9.
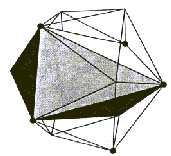
Postopek je potrebno ponoviti še enkrat. Neodvisni niz dveh elementov
je prikazan na Sliki 6.6e. Po izbrisu nastane graf kot na Sliki
6.6f. Zadnja triangulacija (spodnje in zgornje strani) da stanje,
kot je prikazano na Sliki 6.6g. Temu ustreza slika tetraedra na
Sliki 6.10, ki dobi plosko obliko zaradi koplanarnosti vseh štirih
točk, kar je posledica simetričnosti ikozaedra.

Končni rezulatat je torej niz štirih poliedrov P0,P1,P2 in P3, ki so med seboj v hierarhičnem razmerju. Velja PP0P1P2P3. To je osnovno stanje, ki je potrebno za izvedbo algoritma iskanje skrajnih točk poliedra.
Recimo, da je potrebno poiskati najvišjo točko poliedra, to je tisto teme, ki ima največjo koordinato z. Na enak način je mogoče poiskati skrajno točko v katerikoli smeri u.
Naj bo ai najvišja točka poliedra Pi. Potrebno je
poiskati najvišjo točko ak najmanjšega poliedra Pk
in preko te ak-1, ak-2, itd., dokler ni odkrita
točka a0 osnovnega poliedra P0=P. Praktično
to pomeni pomikanje ravnine , ki je pravokotna na z-os,
od točke ak preko ak-1,... do točke a0. Zaradi
omenjenega razmerja med posameznimi poliedri, se ravnina pomika
samo navzgor. Primer je prikazan na Sliki 6.11.
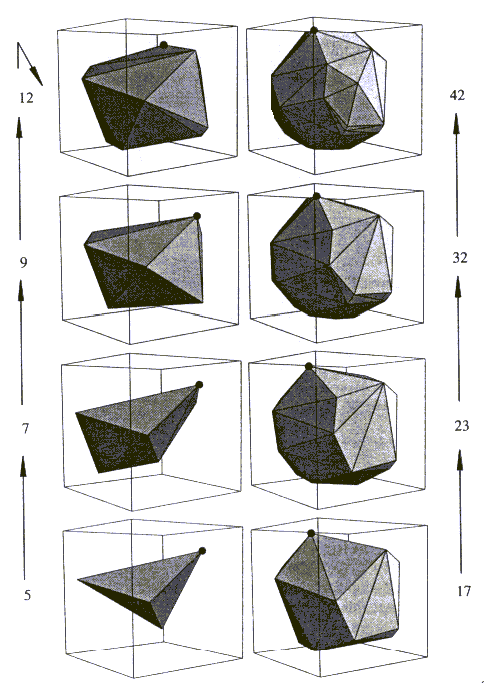
Osnovnega trikotnika n=3 na sliki ni. Ključnega pomena
je torej odnos med točkama ai+1 in ai. Naj bosta
točki ai+1 in ai najvišji točki poliedrov Pi
in Pi+1. Potem je ali ai=ai+1 ali ai+1
najvišje teme med vsemi temeni, ki so sosednja temenu ai.
Razmerje ai=ai+1 je povdarjeno za primer, ko je
ai hkrati najvišje teme obeh poliedrov, Pi in Pi+1.
Pri projekciji poliedra Pi+1 na ravnino, ki je pravokotna
ravnini , ravnino xz, nastane stanje kot je prikazano na
Sliki 6.12.

Ravnina postane premica in polieder Pi+1 postane konveksni mnogokotnik P'i+1. Naj bosta Li+1 in Ri+1 dva robova poliedra Pi+1, ki sta po projekciji sosednja temenu a'i+1 v mnogokotniku P'i+1. Če sta ai in ai+1 edini, najvišji temeni Pi in Pi+1, potem je teme ali ai=ai+1 ali ai najvišje med tistimi temeni, ki izhajajo iz Li+1 ali Ri+1.
Mejno teme konveksnega mnogokotnika je torej določljivo na opisan
način. Najprej je potrebno osnovni polieder P razgraditi
na manjše poliedre. Potem je potrebno najmanjšemu poliedru Pk
poiskati mejno točko ai, ki je določljiva s pomikanjem
ravnine proti u. S pomočjo temena ak je določljivo teme
ak-1, itd., vse do osnovnega poliedra P0, katerega
mejna točka je a0.