ABSTRACT

1. NALOGA

2. OSNOVE TRANSFORMACIJ

3. PRAKTIČEN SISTEM GLEDANJA

4. LITERATURA

NALOGA

Potrebno je razdelati sistem tridimenzionalnega prikaza s pozicioniranjem kamere, fokusa, zavrtitve kamere in oddaljenosti ravnine pogleda.

Sistem vodi v generiranje treh homogenih matrik.

Za enostaven žični model črke F je potrebno predstaviti sistem gledanja in različne primere pogledov s parametri tudi predstaviti.

JEZIK: JavaScript in PHIGS!

OSNOVE TRANSFORMACIJ

Objekti so definirani v svetovnem koordinatnem sistemu, ki je praviloma desno orientirani koordinatni sistem.

Včasih je ugodno, da se objekti definirajo napram lokalnemu koordinatnemu sistemu, za kar obstaja več razlogov. Namreč, ko se modelira tridimenzionalni objekt, je ugodno, da se vozliščne točke gradijo glede na referenčno točko na objektu samem. Pravzaprav ima lahko kompleksen objekt več lokalnih koordinatnih sistemov, po enega za vsak podobjekt. Ker se eden in isti objekt v scenah ponavadi pojavljajo večkrat nam definiranje lokalnih koordinatnih sistemov predstavlja najlažjo pot za oblikovanje scene.

Objekti se v osnovi lahko translirajo, skalirajo ali rotirajo, transformacije pa se opravljajo s pomočjo transformacijskih matrik. Da pa bo način računanja transformacije točk dobljen po enakem principu, je potrebno slednje predstaviti s pomočjo homogenih koordinat. Tako vozlišče V(x,y,z) dobi obliko V'(X,Y,Z,w), za vsak faktor w, ki je različen od nič.

Torej:   x=X/w
            y=Y/w
            z=Z/w

V računalniški grafiki se za faktor w vzame vrednost 1, kar pomeni, da je vektor predstavitve posamezne točke (x,y,z,1). S takšno predstavitvijo točk se transformacije računajo z množenjem posamezne točke s transformacijsko matriko.

TRANSLACIJA:

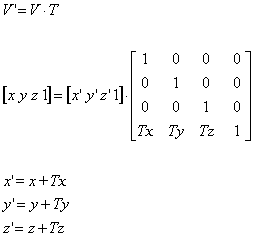
SKALIRANJE:

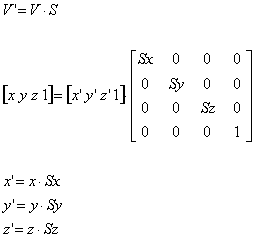
ROTACIJA:

Pri rotacijskih matrikah je potrebno določiti os vrtenja, saj so matrike za vrtenja okoli posameznih osi različne. V našem primeru bo rotacija potekala v nasprotni smeri urinega kazalca.

PRAKTIČEN SISTEM GLEDANJA

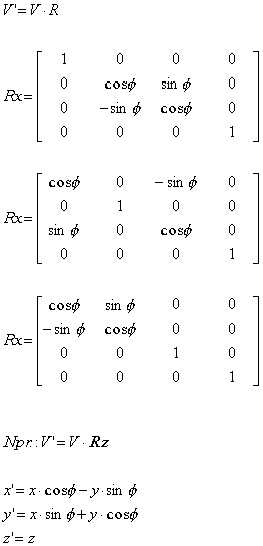
Pri tridimenzionalnih prikazovalnih sistemih nastane problem, če želimo, da je le ta zelo splošen. Ta splošnost sistema pomeni precejšnje naraščanje števila parametrov, ki jih mora uporabnik podati. To pomeni manj pregleden uporabniški vmesnik in računanje transformacijskih točk zahteva kompleksnejše transformacijske matrike.
Kompromisen sistem, ki ne omogoča popolne splošnosti, se pravi, da ima določene omejitve, vendar presega določene najenostavnejšei primere in ima relativno enostaven vmesnik je tako imenovani praktičen sistem gledanja.
Takšen sistem je najbolje predstaviti, če si predstavljamo sintetično kamero v neki točki C=(e,f,g), ki kaže v smeri fokusne točke F=(a,b,c) in je zavrtena za kot Theta (Slika 3). Poleg tega pa je tudi tukaj potrebno vedeti še oddaljenost ravnine pogleda d, kot je to razvidno iz Slike 4.

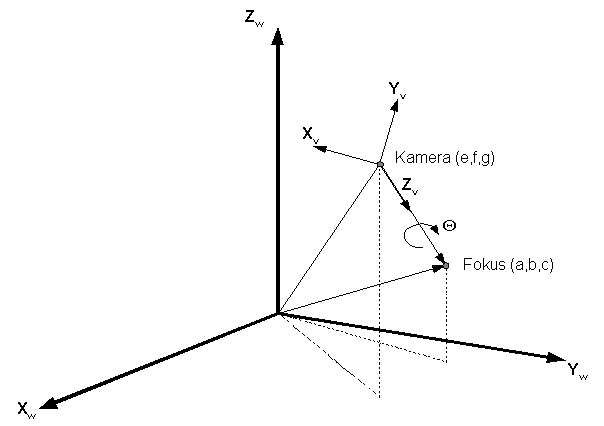
Slika 3

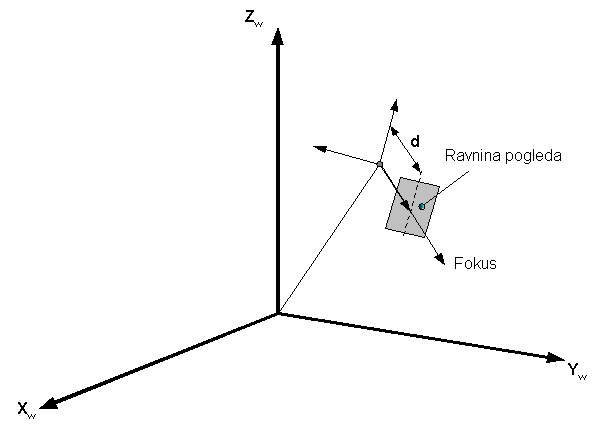
Slika 4

Transformacijska matrika je v tem primeru torej kompleksnejša in je sestavljena iz naslednjih komponent:

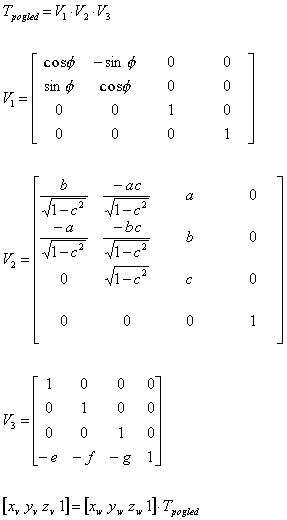
Takšna transformacija bo opravila z večino primerov v računalniški grafiki in se izognila zelo kompliciranim generalnim sistemom prikaza.

Za dodajanje perspektive je potrebna še ena matrika, torej takšna, ki bo dala modelu občutek perspektive. Ta matrika izgleda takole:

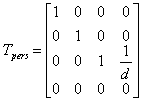
Končno transformacijsko matriko dobimo, ko zmnožimo zgornje matrike med seboj in slednja izgleda takole:

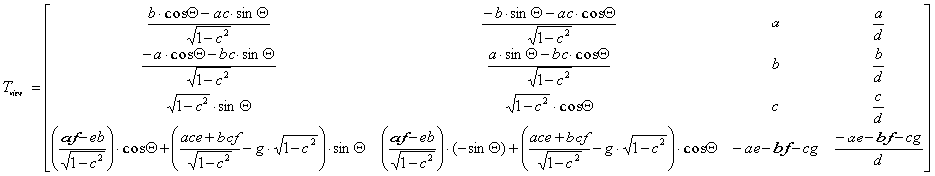
PRIMER PROGRAMA:

PRAKTIČNI SISTEM GLEDANJA

LITERATURA

1.)    WATT, Alan :    FUNDAMENTALS OF THREE-DIMENSIONAL COMPUTER GRAPHICS
                                  Addison-Wesley Publishers Ltd., 1989

2.)    HRIBAR, Peter :   SPOZNAJMO JAVASCRIPT
                                     Flamingo, 1998

3.l.UN - KGS
FAKULTETA ZA STROJNIŠTVO
LJUBLJANA