Planetary transmission drive is drive which at lest one axis with a dental is rotating around central axis.
In machinery designing it is most frequently used designe with three dentals of which are two on the central axis - solar dentals and the third is planetary dental which is rotating around central axis and it is placed on the planetary shaft. Input and output shafts are coaxial, the energy is flowing through the planetary dental and then return toward the central output axis. This is the cause for their name return/reflexsive planetary drives.
Three axsis planetary transmission drives can be coupled into new combine units and some special propertyes would be achived. That kind of planetary transmission drives are called combine planetary drives. With combining at least two simple three axis planetary drives new three axis drive with special propertyes is created. In this case particular drives are called partial drives, conected shafts are called double shafts, individual shafts are single shafts. Torque is carrying outward by only three shafts which are called outer shafts. Torque between partial drives is carrying by one double shaft which is called inner shaft and has no outward influence.
In this seminary is predicate to three axis planetary transmission drives but chapter about combine planetary drives is applyed too. Seminary is based on standard VDI 2157.
Planetna gonila se danes vedno pogosteje uporabljajo in se izkoriščajo v najrazličnejših področjih tehnike. Kot izravnalna gonila so skoraj nepogrešljiva, zasledimo jih povsod kjer se morajo pri majhnih močeh doseči zelo velike prestave, z njimi se prenašajo velike moči pri velikih turažah. Pri primerni izvedbi imajo planetna gonila le polovico volumna stabilnih gonil in boljši izkoristek.
Vsa planetna gonila se lahko predstavijo tudi shematično.
Definicija palnetnih gonil:
Planetna gonila so gonila, pri katerih se vsaj ena os, na kateri je zobnik, vrti okoli centralne osi.
Slika 1)

Najenostavnejši izvedba planetnih gonil imata dva zobnika,kot to prikazuje slika 1. Prva izvedba ima dva zobnika z zunanjim ozobjem, druga pa en zobnik z zunanjim ozobjem in en zobnik z notranjim ozobjem.Pri obeh izvedbah je po en centralni zobnik sončnik A, s pripadajočo gredjo, ena gred z ročico - planetna gred - na njej je os P in en en zobnik planetnik P. Pogon je običajno na planetni gredi odgon pa na planetnku P.
Pri gradnji stroje se mnogo bolj uporabljajo triosna gonila s tremi zobniki, od katerih sta dva na centralnih oseh - sončnika - tretji pa je planetnik, ki je nameščen na planetni gredi ter se vrti okoli centralne osi. Pogonska in odgonska gred ležita koaksialno energija pa se pretaka prako planetnika, ter se vrača na sosednjo gred v centralni osi. Od tu tudi ime Povratna planetna gonila.
Triosna planetna gonila se lahko vežejo tudi v nove kombinirane enote, pri čemer se dajo doseči posebne lastnosti planetnih gonil. Takšna planetna gonila imenujemo sestavljena planetna gonila in jih dobimo, ko povežemo med seboj najmanje dve enostavni triosni planetni gonili tako dobimo ponovno triosno planetno gonilo, ki pa ima svoje posedne lastnosti. Posamezna gonila se v tem primeru imenujejo delna gonila, spojene gredi so dvojne gredi, posamezne gredi so enojne gredi. Vrtilne momente prenašajo navzven samo tri gredi, katere imenujemo zunanje gredi, medtem ko moment med delnimi gonili prenaša ena dvojna gred ki se imenuje notranja gred in navzven ne vpliva.
V tej seminarski nalogi je povdarek predvsem na triosnih palnetnih gonilih v seminarju pa je predstavljena tudi sinteza planetnih gonil. Seminar se navezuje na standard VDI 2157.
PRIMERA PRERAČUNA TRIOSNIH PLANETNIH GONIL
Pri strojih in napravah so zelo ražširjena stabilana gonila, pri katerih vse gredi v prostoru mirujejo. Le ta so enostavnejša za izdelavo, so pa večja in težja od planetnih gonil za enako moč. Pri planetnih gonilih lahko gibanja posameznih gredi združujemo ali pa jih cepimo. Posamezne izvedba planetnih gonil dovoljuje zelo velika prestavna razmerja, kakršna so potrebna pri raznih merilnih in kazalnih napravah (za prenos gibanja pri majhnih silah). Za pretvarjanje vrtenja pri velikih močeh pa se ne uporabljajo.
Nastanek triosnega planetnega gonila si lahko predstavljamo tudi na ta nčin, da dvoosno povratno stabilno gonilo osvobodimo temeljev in damo ohišje ob iztopnih gredeh na ležaje. Obratno pa lahko vsako planetno gonilo spremenimo v stabilnega če planetne gredi fiksiramo, ker pri tem vse osi okrog katerih se vrtijo zobniki mirujrjo.
Triosno planetno gonilo ima tri gredi od katerih je ima planetne gred, na kateri je lahko več osi planetnikov, posebno obliko. Glede na namen gonila in vrsto pogona se vrtita dve gredi in tretja miruje ali pa se vrtijo vse tri gredi.
Razmerje med turažama dveh vrtečih se gredi pri mirujoči tretji gredi imenujemo notranja prestava, razmerje med turažama dveh od treh rotirajočih gredi pa zunanja prestava
Imamo tri možne notranje prestave, ena od teh je, pri mirujoči planetni gredi, stabilna prestava planetnega gonila, medtem ko sta ostali dve planetni prestavi ko miruje ena od dveh sončnih gredi.
Nekaj osnovnih povezav po knjigi Planetna gonila -Jožeta Hlebanje
TRIOSNA PLANETNA GONILA S ČELNIMI ZOBMIKI

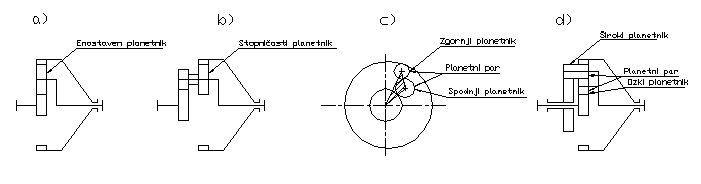
Planetno gonilo prikazano na sliki 1 ima dva sončnika A in B, planetno gred C s planetno osjo p, okrog katere se vrti planetnik P. Sončnik A ima zunanje ozobje, sončnik B pa notranje.

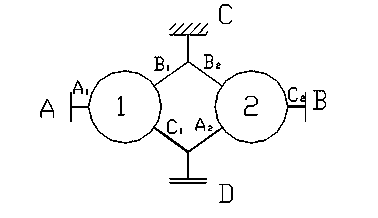
Na sliki 2 imata oba sončnika A in B zunanje ozobje, stopničasto planetno kolo pa ima dva zobnika P1 in P2 z zunanjim ozobjem.

Prav tako so možna triosna planetna gonila s stopničastim planetnikom z dvema zobnikoma z zunanjim ozobjem in dvema sončnikoma z notranjim ozobjem, kot to prikazuje slika 3.
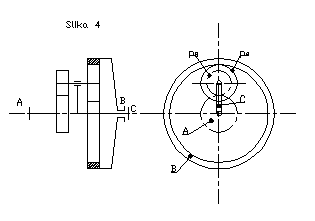
Možna je tudi kombinacija sončnika z zunanjim in sončnika z notranjim ozobjem ter stopničastim planetnikom z dvema zobnikoma kot to prikazuje slika 4.
TRIOSNA PLANETNA GONILA S STOŽČASTIMI ZOBNIKI
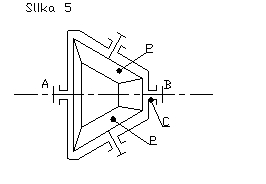
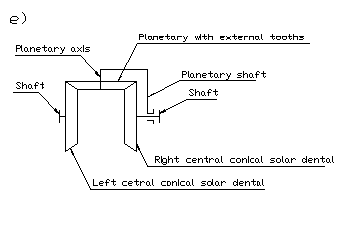
Na sliki 5 je prikazano triosno planetno gonilo s stožčastimi zobniki v osnovi pa so za prenos gibanja med sončnimi gredmi dopustne tudi vse ostale vrste zobatih gonil.
OSNOVNI PRERAČUN TRIOSNIH PLANETNIH GONIL
SPLOšNA PRAVILA
Ker so razmere pri planetnih gonilih lahko tako zelo zamotan, da postane izračun nepregleden je upeljan sistem sistematičnega označevanja posameznih delov, katerega se moramo v celem preračunu dosledno držati.
Gredi so tisti deli po katerih se v gonilo uvaja oziroma odvaja energija. Posamezne veličine kot so turaža, momenti, moč, izkoristki in prestavna razmerja se nanašajo na gredi, zato so njihove označbe še posebej važne.
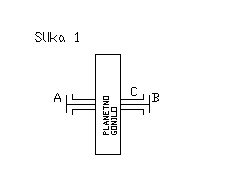
Gonilo na sliki 1 je triosno planetno gonilo z centralnimi gredmi A in B ter planetno osjo C.Veličine, ki se nanašajo na gredi so:
nA, nB, nC - turaže gredi A, B, C.
TA, TB, TC - vrtilni momentui gredi A, B, C.
PA, PB, PC - moč, ki se prenaša po gredi A, B, C.
Notranje prestavno razmerje, katro je razmerje turaž dveh gredi pri mirujoči tretji gredi označimo z "i" in dopolnimi z indeksom gredi, med katerima je prestavno razmerje.

Prestavno razmerje pri mirujoči planetni gredi - stabilna prestava planetnega gonila.

Prestavno razmerje pri mirujoči centralni gredi B (planetna prestava).

Prestavno razmerje pri pri mirujoči središčni gredi A (planetna prestava).

Recipročna vrednost prestavnega razmerja je obrnjeno razmerje turaž gredi.
Kadar se vrtita gredi, med katerima ugotavljamo prestavno razmerje, v isto smer je njihovo prestavno razmerje pozitivno, kadar pa se vrtita v nasprotno pa je negativno.Zaradi boljše ločitve označimo turažo, ko rotirajo vse tri gredi z "m" in pri rotaciji dveh gredi pa z "n".
Zunanja prestava je razmerje dveh turaž, ko se vrtijo vse tri gredi in jo označimo s "k" in dodamo indekse tistih gredi med katerimi je označeno razmerje.

Prestava med gredmi A in C če se vrti tudi gred B.
Gonilo je v ravnotežju, ko so tudi momenti, ki delujejo na posamezne gredi v ravnotežju.


Moč, ki se prenaša po gredi je določena s produktom med vrtilnim momentom in kotno hitrostjo, ki je sorazmerna turaži.

Moč katero gonilu dovajamo označimo kot pozitivno tisto, ki jo pa odvajamo pa kot negativno. Moč je v gedi pozitivna takrat, kadar ima v gredi delujoč vrtilni moment smer vrtenja gredi, kadar pa sta si smeri momenta in vrtenja nasprotni je moč, ki se prenaša po gredi negativna.
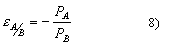
Razmerja moči poameznih gredi. Lahko so negativne ali pozitivne.
Ker je,

Razmerje moči lahko izrezimo tudi:

Zaradi izgub v gonilu je iztopna moč vedno manjša od vstopne moči. če je A vstopna gred in B izstopna potem lahko po enačbi 8) dobimo absolutno vrednost, ki je enaka izkoristku planetnega gonila. če upoštevamo izgube moramo za gonilo ki ima dve vrteči gredi zapisati.

Iz pogoja v enačbi 6) sledi, da mora biti tudi v tretji gredi vrtilni moment, ker pa miruje se moč po njej ne prenaša. Enačbe 8 in 11 veljajo analogno tudi za gredi A/C in B/C.
Ko ugotavljamo potek moči k zobniku in proč od njega, poznamo silo, ki deluje na zobnik in obodno hitrost vrtenja zobnika. če sta sila na zobnik in obodna hitrost enako usmerjeni, moč zobniku dovajamo, ko pa sta usmerjeni nasprotno, moč od zobnika odvajamo.
PRERAČUN HITROSTI
PRERAČUN HITROSTI IN TURAŽE
Obodne hitrosti postanejo zelo pregledne v diagramu hitrosti če ga narišemo v ustreznem merilu, ponavadi z merilom Ld za premer zobnika in Lv za obodno hitrostrost ponazorjeno z dolžinskimi enotami.

Pri danem radiju delilnega kroga zobnika in kotni hitrosti je obodna hitrost



Tako doibmo vrtljaje n glede na odmerjeno dolžino Ln ki je enaka 1/min na izbrano dolžinsko enoto.
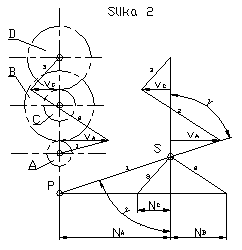
Vsa ta pravila pa veljajo tudi za več zobnikov v prijemu kot je to pokazano na sliki 2). Iz diagrama hitrosti lahko razberemo, da sta obodni hitrosti dveh zobnikov v prijemu enaki.
če iz točke S narišemo vzporednice premic, ki potekajo od središč zobnikov do konic vektorjev hitrosti, potem te vzporednice sekajo premico "p" v dolžinah, ki so proporcionalne turažam posameznih zobinkov.
Primer diagrama hitrosti za enostavno planetno gonilo.
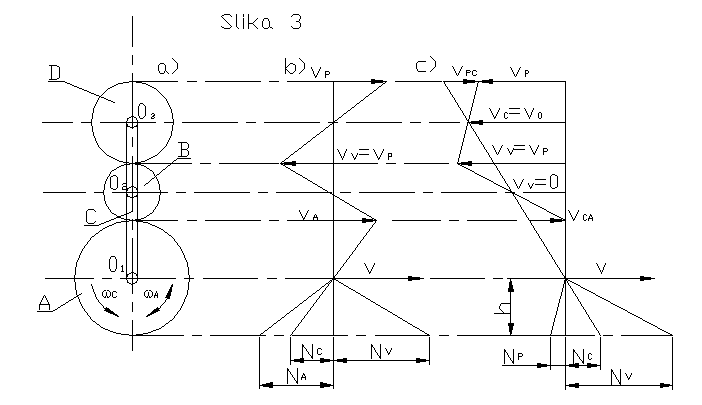
Slika 3) prikazuje: a) shemo gonila, b) diagram hitrosti za primer ko ročica C miruje zobnik A pa se vrti z neko kotno hitrostjo. Osi vseh treh zobnikov v prostoru mirujejo, obodne hitrosti v teh točkah pa so enake nič, zato morajo biti tudi črte, ki predstavljajo diagram obodne hitrosti potekati v višini osi zobnikov skozi točke, ki predstavljajo hitrosti. Slika c) prikazuje primer, ko celotno gonilo rotira s kotno hitrostjo  . Pri tem preide gibanje zobnika A v mirovanje. Hitrostno stanje zobnikov je tako kot če bi se vrtela ročica C z neko kotno hitrostjo pri mirujočem zobniku A. Obodne hitrosti so v dotikališčih zobnikov za oba zobnika enake.
. Pri tem preide gibanje zobnika A v mirovanje. Hitrostno stanje zobnikov je tako kot če bi se vrtela ročica C z neko kotno hitrostjo pri mirujočem zobniku A. Obodne hitrosti so v dotikališčih zobnikov za oba zobnika enake.
Enako postopamo pri gonilih, pri katerih osi koles niso v isti ravnini. Izhajati moramo iz znanih obodnih hitrosti. Shema take gonila je na zgornji sliki 4). Slika 4) a) prikazuje diagram hitrosti za stabilno gonilo. Osi zobnikov, ki niso v ravnini nato zarotiramo na ordinato diagrama in z njimi tudi vektorje obodnih hitosti slika b). Pri planetni prestavi  , preide kolo A v mirovanje, relativna hitrost nasproti ročice C pa ostane nespremenjena.
, preide kolo A v mirovanje, relativna hitrost nasproti ročice C pa ostane nespremenjena.

Pri stožčastih zobnikih si z diagrami hitrosti ne moremo pomagati zato pa si lahko ponazorimo razmere vrtenja z vektorji, ki predstavljajo kotne hitrosti. Pri preračunu uporabimo pravilo o seštevanju rotacij okoli sekajočih se osi.  Velikost in smer vektorja sta določena z mnogokotnikom hitrosti lega pa s presečiščem osi. Vse osi se morajo sekati v skupni točki. Kotna hitrost zobnika B proti zobniku A je podana na tvornici M vse tri osi se sekajo v isti točki.
Velikost in smer vektorja sta določena z mnogokotnikom hitrosti lega pa s presečiščem osi. Vse osi se morajo sekati v skupni točki. Kotna hitrost zobnika B proti zobniku A je podana na tvornici M vse tri osi se sekajo v isti točki.

PRERAČUN PRESTAVNIH RAZMERIJ
PRERAČUN PRESTAVNEGA RAZMERJA PRI DVEH ROTIRAJOČIH GREDEH
(Notranje prestavno razmerje)

Notranje prestavno razmerje planetnega gonila je določeno z razmerjem turaž dveh gredi pri mirujoči tretji gredi. A in B sta gredi sončnikov, gred C pa je planetna gred. Pri troosnem planetnem gonilu imamo torej tri notranje prestave, od katerih predstavlja ona z mirujočo planetno gredjo stabilno prestavo. Definicija za notranje prestave (Scwampovo pravilo) velja za vsa planetna gonila, ne glede na to kako so gredi med seboj povezane. Važno je le to da se sončniki ubirajo s planetniki in da so planetniki nameščeni na na ročiči planetne gredi. Na spodnji sliki sta A in B gredi sončnikov, gred C pa je planetna gred. Označba je popolnoma poljubna in je namenjena samo razlagi gonilnika. Stabilna prestava iA/B je odvisna samo od geometrijskih razmer gonila (števila zob in premerov zobnikov).
Ko določamo notranjo prestavo moramo eno od gredi ustaviti, ali pa poiskati relativne turaže obeh gredi nasproti tretji gredi. Pri stabilni prestavi mora mirovati gred C.Če želimo dobiti neko drugo notranjo prestavo mora mirovati neka druga gred. Če želimo notranjo prestavo med A in C mora mirovati gred B. Od mirujoče prestave C pri stabilni prestavi, do mirujoče gredi B pridemo tako, da vrtimo celotno gonilo s turažo -nB. Tako dobi gred A turažo nAB=nA-nB in gred C, n'C=-nB. Iz tega sledi notranja prestava:

Na enak način pridemo do notranje prestave med gredma B in C, le da mora pri tem mirovati gred A. Do tega pridemo če vrtimo celo gonilo z -nA. Pravilo za določanje notranjih prestav se imenuje Schwampovo pravilo.
Iz enačb vidimo, da je notranja prestava med gredma A in C določena z notranjo prestavo med gredma A in B. Iz enčb je razvidno, da je triosno planetno gonilo glede notranjih prestav popolnoma določeno, če poznamo eno notranjo prestavo. Po schwampovem pravilu lahko vsako notranjo prestavo izračunamo iz ene od ostalih dveh notranjih prestav.

Ena od notranjih prestav mora imeti nasproten predznak. Vsako notranjo prestavo pa lahko izrazimo z ostalima dvema.

Glede na predznak ločimo planetna gonila s pozitivno in planetna gonila z negativno stabilno prestavo. Funkcijska odvisnost med planetno prestavo in stabilno prestavo je linearna.
Pri stabilni prestavi iA/B=1 se vrtita pogonska in odgonska gred enako, tako gonilo deluje kot sklopka. ( Primer je,ko imamo planetno gonilo s samo dvema gredma A in C in se planetni zobnik na gredi C ne vrti - ležaji planetnega zobnika so blokirani - zato se gred A lahko vrti samo z enako turažo.) Ko pa je iA/B=-1 se vrtita z enako turažo v nasprotni smeri. Ker se v območju -1< iA/B < 1 predznaki menjajo imenujemo to območje obračalno območje.
Notranja prestavna razmerja lahko določimo tudi iz diagrama hitrosti vendar se ta metoda uporablja samo za reševanje posebnih nalog, ker nimamo skupnih pravil, ki bi velja za vsa gonila.
če upoštevamo, da imajo zobniki, ki so v ubiranju enak modul in neko število zob potem lahko določimo po teh enačbah izračunamo prestavo z upoštevanjem števila zob enačbe 5). Pri preračunu je treba paziti na predznak prestave. V primeru, ko imamo tri gredi in pogon na eni od sončnih gredi je glede na planetno os vrtenje druge sončne gredi nasprotno vrtenju prve zato ima lahko prestava iA/C negativen predznak, enačba 5) b). V primeru ko imamo dvojni stopničast planetnik pa se ta prestava izrazi po enačbi 5) c).

Ena od gredi v takem gonilu je obremenjena z vsoto momentov ostalih dveh gredi tako gred imenujemo sumarna gred, ostali gredi pa diferenčni gredi. Sumarna gred je tista, ki da pri mirovanju negativno prestavo ostalih dveh gredi.Sumarna gred je lahko planetna gred ali ena od sončnih gredi.
Triosno planetno gonilo lahko prikažemo s simbolično shemo Slika a), to je krog s tremi žarki, ki predstavljajo gredi A,B in C.
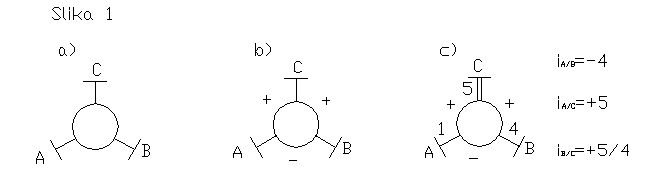
če momente na posameznih gredeh delimo z najmanjčim izmed njih dobimo specifične moment. Pri gonilu brez izgub je tudi razmerje specifičnih momentov enako prestavnemu razmerju. Večji momenti pripadajo počasnejšim gredem. K gredem na shemah lahko pripišemo še specifične momente in predznak notranje prestave dotičnih gredi (Slika b in c) lahko takoj ugotovimo prestavna razmerja. Ker je sumarna gred tista, ki pri negativni prestavi miruje jo v shemi označimo z dvem ačrtama in leži nasproti minusa.
PRERAČUN PRESTAVNEGA RAZMERJA PRI TREH ROTIRAJOČIH GREDEH
(Zunanje prestavno razmerje)
Zunanja prestava je razmerje turaž dveh gredi če se vse tri gredi vrtijo. Od notranje prestave pridemo do zunanje če vse tri gredi vrtimo. Ko planetno gonilo vrtimo še s turažo mCdobi gred A turažu  in gred B turažo
in gred B turažo  . V takem primeru lahko prosto izbiramo turažo mC in s tem dobimo poljubno zunanjo prestavo. Iz tega sledi da planetno gonilo z eno zunanjno prestavo gonilo še ni določeno zato ima vsako planetno gonilo s tremi rotirajočimi gredmi tri zunanje prestave.
. V takem primeru lahko prosto izbiramo turažo mC in s tem dobimo poljubno zunanjo prestavo. Iz tega sledi da planetno gonilo z eno zunanjno prestavo gonilo še ni določeno zato ima vsako planetno gonilo s tremi rotirajočimi gredmi tri zunanje prestave.
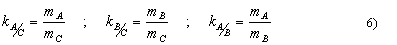
Zvezo med notranjimi in zunanjimi prestavami dobimo, ko tvorimo razmerje relativnih turaž proti gredi, ki naj pri notranji prestavi miruje.
Notranjo prestavo med gredma B in C odbimo, ko tvorimo razmerje relativnih hitrosti proti gredi A (po Schwampovem pravilu).

Na enak način lahko dobimu tudi ostali dve notranji prestavi:
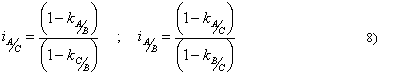
Iz prikazanega sledi, da lahko vsako notranjo prestavo dobimo z dvema zunanjima prestavama. Planetno gonilo je z eno notranjo prestavo enolično določeno in v enako meri z dvema zunanjima. Zunanje prestave so med seboj v razmerju:

Iz tega sledi, da morajo imeti vse tri prestave enak predznak, kar pomeni, da se vse tri gredi vrtijo v isto smer. Za vsako turažo pri treh rotirajočih gredeh lahko vzamemo, da je sestavljena iz dveh turaž.
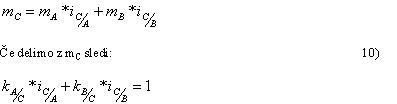
Razmerje med vrtilnimi momenti na posameznih gredeh je odvisno od notranjih prestav, zato zunanje prestave ne določajo odnosov med vrtilnimi momenti.
PRERAČUN MOČI
PRERAČUN MOČI PRI PRENAŠANJU MED GREDMI BREZ UPOŠTEVANJA IZGUB
(Pri dveh rotirajočih gredeh)
V primeru ko računamo iA/B in pri mirujoči sončni gredi B, nas zanimjo relativne hitrosti nasproti planetne gredi in sistemska hitrost na gredi C - planetna gred. Ko hitrosti pomnožimo s silami oziroma momente na gredeh s turažami dobimo moči, ki se po posameznih gredeh prenašajo. Moči, ki ustrezajo relativnim hitrostim se prenašajo med zobniki, tako kot pri stabilnem gonilu, s kotaljenjem, medtem, ko ustrezajo sistemske hitrosti razmeram pri sklopki. Moč, ki pri planetnih gonilih ustreza relativnim hitrostim je kotalna moč moč, moč ki ustreza sistemskim hitrostim pa je sklopna moč. Pri vsakem planetnem gonilu pri katerem nastopa relativna hitrost nasproti planetni gredi in pri kateri je hitrost planetne gredi sistemska hitrost, nastopata tudi kotalna in sklopna moč. MoČ kotaljenja, ki se po gredi prenaša je določena z vrtilnim momentom na gredi in relativno turažo proti planetni gredi, sklopna moč pa je določena z enakim momentom in turažo planetne gredi. Vsota obeh moči, ki se vodita preko gonila, mora biti enaka dovedeni oziroma odvedeni moči.

Ko tvorimo razmerje kotalne in sklopne moči dobimo razmerje:

Iz enačb 2) in 3) vidimo, da se da razmerje kotalne oziroma sklopne moči proti delovni izraziti s prestavnim razmerji. je enak notranji prestavi med planetno gredjo in mirujočo sončno gredjo,
je enak notranji prestavi med planetno gredjo in mirujočo sončno gredjo, 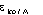 pa je enak notranji prestavi med planetno gredjo in sončno gredjo po kateri se moč dovaja.
pa je enak notranji prestavi med planetno gredjo in sončno gredjo po kateri se moč dovaja.
Vsota členov v enačbi 4) je ena to dosežemo, ko je :
1) vsota vsakega izmed sumandov med ena in nic.
2) ko je vrednost enega sumanda pozitivna in večja od ena, ter drugega sumanda negativna.
V prvem primeru se dovedena moč deli na dva dela. En del se prenaša s kotaljenjem drugi del pa kot pri sklopki. V drugem primeru pa se po nekaterih delih gonila vodi večja moč kot je bila dovedena. V prvem primeru govorimo o delitvi moči v drugem primeru pa o jalovi moči.
Iz enačbe 3) sledi, da se po gonilu moč deli takrat, ko velja  in
in 
Jalova moč se pojavi v dveh primerih in sicer, ko je kotalna moč večja od dovedene moči ali pa, ko je sklopna moč večja od dovedene.
Primera dveh povezav s simboličnimi shemami.

Pri zgornjem gonilu se pojavlja jalova moč, moč, ki s eprenaša kakor pri sklopki, deluje v nasprotni smeri kakor dovedena moč in se prenaša samo med določenimi deli gonila. Iz tega je razvidno, da morajo nekateri deli prenašati večjo moč in morajo biti tudi temu ustrezno dimenzionirani. Tako poteka moč pri gonilih, pri katerih je izstopna moč gred diferenčna gred, sumarna gred pa fiksirana.

Pri zgornjem gonilu se tudi pojavlja jalova moč. Pri teh gonilih je sklopna moč večja od dovedene moči, kotalna moč pa teče v nasprotni smeri kot sklopna, zato se imenujejo taka gonila protitočna gonila. Pri takih gonilih morajo biti deli, ki so podvrženi obrabi dimenzionirani na kotalno moč, deli za katere pa je merodajna trdnost pa na sklopno moč.
PRERAČUN PRENOSA MOČI PRI TREH ROTIRAJOČIH GREDEH
(Brez upoštevanja izgub)
Moč, ki se prenaža po gredeh triosnega planetnega gonila je odvisna od vrtilnih momentov, ki delujejo v posameznih gredeh in pripadajočih turaž. Vrtilni momenti so dani z zunanjo obremenitvijo, njihova porazdelitev na posamezne gredi pa je določena z geometrijsko obliko gonila.
Turaže pri treh rotirajočuih gredeh se lahko spreminjajo s tem pa se spreminjajo tudi moči v posameznih gredeh. Moči pa se lahko spreminjajo tako, da je gonilu dovedena moč enaka odvedeni moči. Moč v posameznih gredeh je :

V tej enačbi mora imeti en člen drugačen predznak od ostalih, kar pomeni, da se moč po dveh gredeh dovaja po eni pa odvaja ali obratno.

Planetno gonilo na sliki ima sumarno gred C, moment na njej deluje nasprotno od momentov na gredeh A in B. Vse gredi pa se vrtijo v isti smeri.
Iz smeri vrtenja momentov ugotovimo, da se na gredi A in B moč dovaja, an gredi C pa odvaja. Po enačbi

Lahko vidimo, da turažo gredi C lahko sestavimo iz dveh sumandov. Ko obe strani enačbe pomnožimo z vrtilnim momentom na gredi C dobimo

Prvi sumand desne strani predstavlja moč, ki je bila dovedena gredi C iz gredi A, drugi sumand pa moč, ki je bila dovedena gredi B. Ta enačba nam pove, da se da obravnavati vsak del toka moči ločeno ter da predstavlja vsak sumand tisti del moči, ki se prenaša med dvema gredema pri mirujoči tretji gredi. Mirujoča je tista gred, ki v obravnavanem sumandu ni zastopana s svojim indeksom. S tem smo planetno gonilo s tremi rotirajočimi gredmi pretvorili v dve planetni gonili z dvema rotirajočima gredema in to v delno gonilo pri katerem miruje gred B in delno gonilo pri katerem miruje gred A. Taka planetna gonila se računa po enačbah iz dela, ki govori o planetnih gonilih, ki imajo dve rotirajoči gredi.
PRERAČUN PRENOSA MOČI PRI TREH ROTIRAJOČIH GREDEH
(Z upoštevanjem izgub)
Izgube so odvisne samo od moči, ki se med posameznimi gredmi prenaša s kotaljenjem. Pri znani vstopni in izstopni oči gonila lahko izrašunamo vrtilne momente na teh gredeh oziroma njihovo medsebojno razmerje. Tako dobljene razmerje momentov posameznih gredi se pri dodatnem vrtenju gonila ne spreminja.
Iz razmerja:

Ker pri stabilni prestavi gred C miruje, je moč v tej gredi PC=0, kljub temu, da je ta gred obremenjena z momentm TC. Pri prenašanju moči od gredi A k gredi B nastanejo energeijske izgube V, ki so posledica trenja med zobmi in trenja v ležajih. Če sedaj pri danih obremenitvah gredi (TATBTC) vrtimo vse tri gredi z enakimi turažami mC, dobimo produkt iz momentov in dodatne turaže mC moči, ki se dodatno prenašajo po gredeh. Pri tem dodatnem vrtenju deluje gonilo kot sklopka med posameznimi deli gonila. Razen v ležajih, ni nobenega gibanja zato tudi ni nobenih izgub. Iz smeri vrtenja momentov in turaž se da takoj ugotoviti na katerih gredeh se moč dovaja in na katerih se moč odvaja. Če vrtenje stabilnega gonila in dodatno vrtenje seštejemo, dobimo novo stanje vrtenja pri katerem pa se velikost in smer vrtenja momentov nista spremenila. Produkti iz rezultirajočih turaČ in momentov pa dajo moč, ki se pri treh rotirajočih gredeh po njih vodi. Do enakega rezultata pridemo, če seštejemo moči, ki se vodijo po gredeh pri stabilni prestavi in pri dodatnem vrtenju. Pri tem bi ugotovili, da se izgube, ki so nastale pri stabilni prestavi niso spremenile. V matematični obliki se dajo moči na posameznih gredeh izraziti tako:

Ko izračunamo razmerje med odvedenimi in dovedenimi močmi, dobimo izkoristek gonil.

Kadar izberemo tako dodatno turažo, da pride ena od sončnih gredi do mirovanja, dobimo planetno prestavo, ki more biti sama po sebi primer gibalnega stanja pri treh rotirajočih gredeh.




























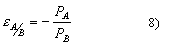








 . Pri tem preide gibanje zobnika A v mirovanje. Hitrostno stanje zobnikov je tako kot če bi se vrtela ročica C z neko kotno hitrostjo pri mirujočem zobniku A. Obodne hitrosti so v dotikališčih zobnikov za oba zobnika enake.
. Pri tem preide gibanje zobnika A v mirovanje. Hitrostno stanje zobnikov je tako kot če bi se vrtela ročica C z neko kotno hitrostjo pri mirujočem zobniku A. Obodne hitrosti so v dotikališčih zobnikov za oba zobnika enake.


 Velikost in smer vektorja sta določena z mnogokotnikom hitrosti lega pa s presečiščem osi. Vse osi se morajo sekati v skupni točki. Kotna hitrost zobnika B proti zobniku A je podana na tvornici M vse tri osi se sekajo v isti točki.
Velikost in smer vektorja sta določena z mnogokotnikom hitrosti lega pa s presečiščem osi. Vse osi se morajo sekati v skupni točki. Kotna hitrost zobnika B proti zobniku A je podana na tvornici M vse tri osi se sekajo v isti točki.






 in gred B turažo
in gred B turažo  . V takem primeru lahko prosto izbiramo turažo mC in s tem dobimo poljubno zunanjo prestavo. Iz tega sledi da planetno gonilo z eno zunanjno prestavo gonilo še ni določeno zato ima vsako planetno gonilo s tremi rotirajočimi gredmi tri zunanje prestave.
. V takem primeru lahko prosto izbiramo turažo mC in s tem dobimo poljubno zunanjo prestavo. Iz tega sledi da planetno gonilo z eno zunanjno prestavo gonilo še ni določeno zato ima vsako planetno gonilo s tremi rotirajočimi gredmi tri zunanje prestave.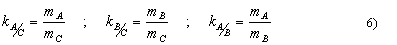

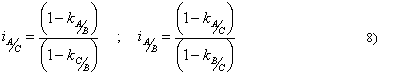

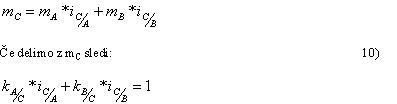


 je enak notranji prestavi med planetno gredjo in mirujočo sončno gredjo,
je enak notranji prestavi med planetno gredjo in mirujočo sončno gredjo, 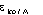 pa je enak notranji prestavi med planetno gredjo in sončno gredjo po kateri se moč dovaja.
pa je enak notranji prestavi med planetno gredjo in sončno gredjo po kateri se moč dovaja. in
in 










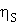 . To je izkoristek planetnega gonila pri stabilni prestavi z upoštevanjem vseh zobnikov, ki ubirajo. Če ima planetno gonilo pri stabilni prestavi dvakratni vprijem je
. To je izkoristek planetnega gonila pri stabilni prestavi z upoštevanjem vseh zobnikov, ki ubirajo. Če ima planetno gonilo pri stabilni prestavi dvakratni vprijem je  pri čemer pa je
pri čemer pa je 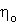 izkoristek med dvema zobnikoma. Za dobro obdelane zobnike velja
izkoristek med dvema zobnikoma. Za dobro obdelane zobnike velja  . Izgube in izkoristek triosnega planetnega gonila lahko izrazimo z dovedeno močjo:
. Izgube in izkoristek triosnega planetnega gonila lahko izrazimo z dovedeno močjo:







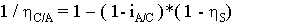
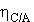 samo v tem območju.
samo v tem območju.