TOK IDEALNEGA FLUIDA

1. DEFINICIJA NALOGE

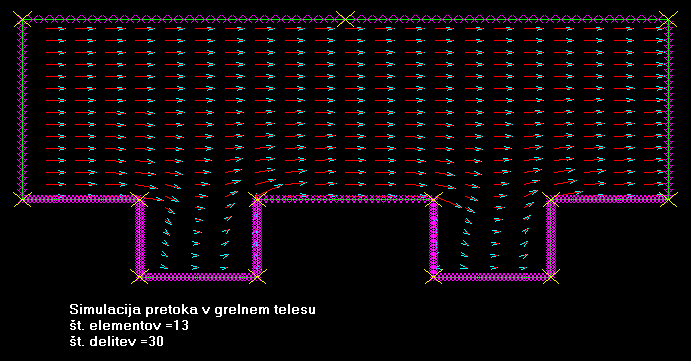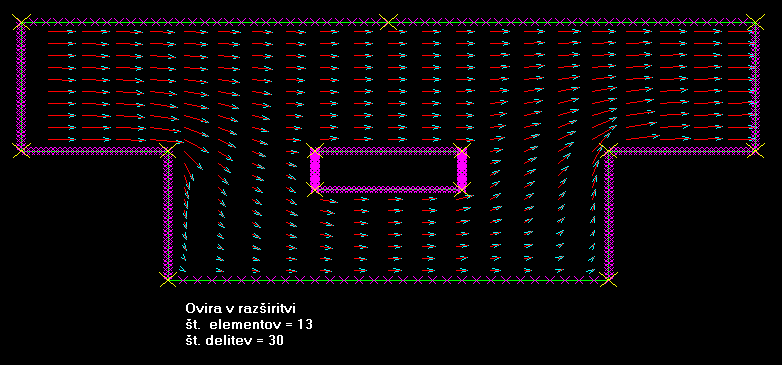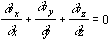
Izdelajte program za izračun ravninskega stacionarnega toka nestisljivega in neviskoznega fluida. Fluid naj se pretaka v mejah poljubne oblike. Rešitve enačbe in hitrostno polje v izbranih točkah prikažite z uporabo grafičnega standarda Phigs .

2. TEORETIČNE OSNOVE

2.1 Kontinuitetna enačba

Kontinuitetna enačba za nestisljiv fluid :

2.2 Hitrostni potencial

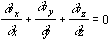
Za potencialni oziroma nevrtinčni tok poznamo Laplacevo enačbo, ki opisuje potencialno polje brez notranjih izvorov :

2.3 Metoda robnih elementov

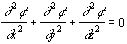
Metoda robnih elementov je najprimernejša numerična metoda za reševanje potencialnih problemov kot jih prikazuje Laplaceova enačba.

Pri metodi robnih elementov rešujemo enačbo na elementih na robu potencialnega območja in na podlagi teh rezultatov, lahko za vsako točko znotraj polja izračunamo potencial.

2.4 Robni elementi

Krivuljo k, ki predatavlja ograjo območja D, diskretiziramo na enostavne elemente, ki jih nato integriramo.

2.5 Numerično integriranje

Numerična integracija funkcije f(x) v mejah a do b je rešitev integrala kadar ni znana točna analitična rešitev. V nalogi se uporablja Gauss-Legrendova kvadraturna metoda, ki hitro da natančen rezultat.

Splošna enačba Gauss-Legrendove metode je:

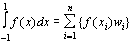
Za poljubno območje integracije podintegralske funkcije z Gaussovo metodo moramo območje (-1,1) prvesti s pomočjo skaliranja s in translacije t.

Integracija se vrši tako, da se v n točkah vzame vrednost funkcije f(x), ki se jo pomnoži z utežjo w. Vsota obteženih funkcij je vrednost integrala.

Integral poljubnih mej izračunamo po naslednji formuli:

3. Primer

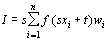
Vhodna datoteka ima v prvi vrstici podano število diskretiziranih elementov roba k in število nadalnih delitev teh elementov. V drugi in vseh nadaljnih vrsticah pa so koordinate (2-D) začetne in končne točke ter kot peto število hitrost na robu (predznak "-" pomeni, da tok priteka).

primer:

00 00 06 00 0
06 00 14 05 -1
14 05 20 00 0
20 00 20 10 0
20 10 14 10 0
14 10 06 10 1
06 10 00 10 0
00 10 00 00 0
05 03 15 03 0
15 03 08 06 0
08 06 05 03 0

3.1 Kontrola notranjosti lika

Ker je lik-ograja poljubne 2D oblike moramo kontrolirati notranjost točk, ki jih določimo. To kontrolo vršimo na način, ali je število pretezov območja, ki ga reže daljica iz izbrane točke sodoali liho. Če je sodo, je točka zunanja ter če je liho, je točka notranja.

3.2 Množenje martik - reševanje sistema enačb

Sistem enačb rešujemo po metodi Lower-Upper dekompoziciji, ki se sestoji iz dveh delov:

decomposition - razdeli matriko na dva dela (zgornja/spodnja)
backsubstitution - množi desno stran enačbe z zgornjo matriko in izračunava neznane linearne vrednosti.

Za ta del izvajanja sem uporabil že kar standardna programa :

Lubksb.for

Ludcmp.for.

5. Delovanje progama

Program je sestavljen dveh delov

1 Glavni program: TOK.for

1.1 Branje vhodne datoteke Vhod.txt,0

1.2 Razdelitev datoteke Vhod.txt na število delitev in zapis vnovo datoteko Del.txt,

1.3 Izračun dolžin elementov

Dolžine elementov se izračuna kot razdalja med dvema točkama (vektorjema).

1.4 Dolčitev točki zvorov na sredini delitve

Izvorne točke ležijo na sredini dolžine elementov.

1.5 Določitev normal na elemente

1.6 Iračun matrik H in G (s pomočjo podprogrma IntGauss)

Podprogram IntGauss izvede integriranje posameznih koeficientov matrik H in G tako, da vsak izvor integrira po celem robu in za vsak element izvede gaussovo kvadraturo vštirih točkah.

1.7 Izračun potenciala na ograji (s pomočjo podprogramov Ludcmp.for in Lubksb.for)

1.8 Določitev točk v notranjosti območja

Z izračun potencialnega polja v notranjost moramo določiti katere točke se nahajajo v notranjosti. To ugotovimo, da za vsako točko nekoliko večje mreže od ograje, kontroliram število presekov območja (liho-notranjost, sodo- zunanjost).

1.9 Izračun potenciala v notranjosti (s pomočjo podprogramov Intgauss in Presek)

1.10 Izračun hitrosti Vx in Vy znotraj območja

Hitrost v točki je kar razlika potencialov sosednjih točk deljena s razdaljo med sosednjima točkama.

1.11 Zapis koordinat točk in vektorjev hitrosti v točkah v datoteko Smer.txt.

2 Program za izris tokovnic fluida - Phigs standard: GRAF2D.for

2.1 Branje datoteke Vhod.txt

2.2 Branje datoteke Del.txt

2.3 Branje datoteke Smer.txt

2.4 Odpiranje grafične knjižnice Phigs

2.5 Izračun kordinat puščic vektorjev hitrosti

2.6 Izris puščic

2.7 Izris vektorjev hitrosti (podatki so v Smer.txt)

2.8 Izris ograje območja (podatki so v Vhod.txt)

2.9 Izračun točk križcev na mestu delitev elementov

2.9.1 Izris točk delitev s križci

2.10 Izračun točk križcev na začetku in koncu elementov

2.10.1 Izris točk elementov s križci

2.11 Zapiranje grafične knjižnice Phigs

6. Zaključek

Vaja Tok idealnega fluida je zahtevala uporabo datotek in numeričnih metod za integracijo in reševanje sistema linearnih enačb. Za grafični del sem tudi uporabljal standard Phigs, ki je nazorno prikazal delovanje grafike.

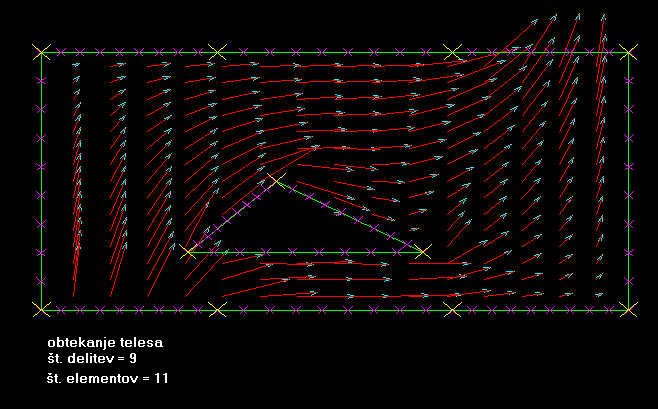
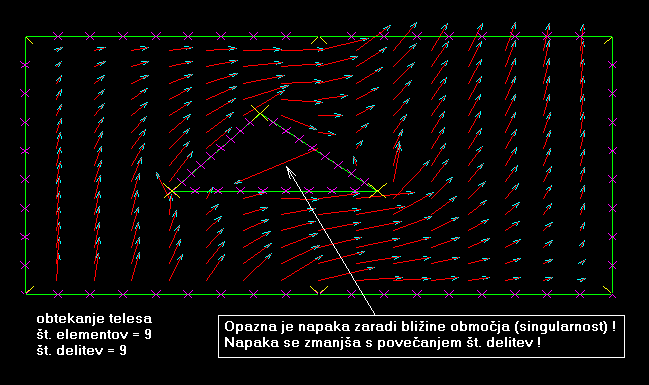
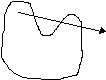
Za testni primer sem vzel kar šolslki primer, s tem, da sem znotraj ograje dodal ograjo v obliki trikotnika. Testiranje tega primera pokaže tokovnice idealnega fluida, ki obtekajo trikotnik, znotraj nekega pravokotnika v katerega spodaj priteka fluid, zgoraj pa odteka iz njega.

7. Literatura

- Zdravko Dovedan, Fortran 77, 1987

- Leon Kos, predloga za vajo Tok idealnega fluida, LECAD 1997

- Leon Kos, Emulacija knjižnice PHIGS, LECAD 1997

- J. N. Bronštejn - K. A. Semedjajecv, Matematični priročnik,1984

- J. Trevelyan, Boundery Elements for Engineers, 1994

- C. A. Brebbia, The Boundery Elements Method for Engineres

8. Rešeni primeri

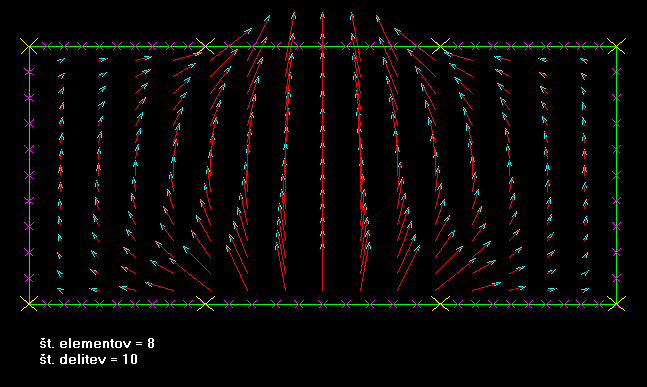
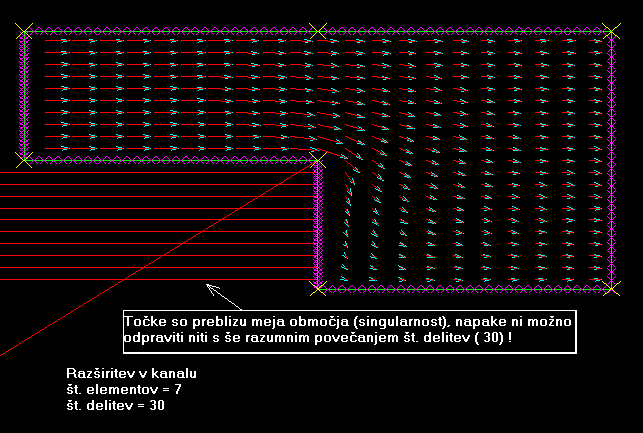
Pikazanih je več primerov, ki so zgolj teoretični, nekaj pa je tudi takšnih, ki imajo tudi prktično veljavo iz strojniškega okolja.

Vabimo Vas, da si ogledate naslednje prikazane modele.