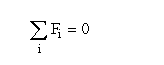
PREDSTAVITEV PRINCIPOV DELOVANJA PROGRAMA
PREDSTAVITEV PRINCIPOV DELOVANJA PROGRAMA
OMEJITVE IN POMANKLJIVOSTI PROGRAMA
Dandanes izgublja svojo vlogo klasicen izracun palicij zaradi prevelikega obsega palic oz. vozlisc. Izracun na klasicen nacin bi bil dolgotrajen; to pa si danes podjetja ne morejo privosciti. To je glavni razlog za uporabo numericnih algoritmov, ki se jih da uporabiti na racunalnikih (manjsi primeri) ali na delovnih postajah (vecji primeri). Numericne metode so omogocile obravnavo napetostno-deformacijskih stanj na matematicno nepravilnih oblikah konstrukcij.
Najbolj primerna in tudi najbolj uporabljena numericna metoda za resevanje omenjenih problemov je metoda koncnih elementov (MKE), ki sem jo uporabil na danem primeru.
V nasem primeru je glavni razlog za uporabe te metode hitrost izracuna.
Izdelaj program za izracun staticno dolocenih in staticno nedolocenih palicij. Vhodni podatki naj bodo podani v datoteki. Oblika vhodnih podatkov je prikazana v predlogi. Program naj napravi izracun, rezultate pa naj zapise v izhodno datoteko (palpost.txt v mojem primeru). Izhodna datoteka naj vsebuje podatke, ki jih bo potreboval postprocesor za graficni prikaz.
Kot sem ze v uvodu omenil, je osnova za izracun MKE. Metoda temelji na prenosnih matrikah, ki prenasajo oz. transformirajo silo iz enega vozlisca preko elementa do drugega vozlisca. V nasem primeru je ta transformacija zelo enostavna, ker je sila po vsem elementu konstantna. Sila v palici je:
F=(Dl/l)EA
kjer je:
Raztezek palice dl nadomestimo s totalnim diferencialom dl (predloga enacba 3 in 4). Sile razcepimo na posamezne komponente (predloga enacba 5).
V vsakem vozliscu morajo biti sile v ravnotezju.
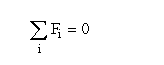
Prav tako pa mora biti zadosceno sistemu enacb, ki ga simbolicno prikazemo z naslednjo enacbo:
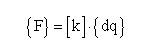
kjer predstavlja:
To so grobe teoreticne osnove, ki pa so osnova za izracun problema.
Prototipi so navedeni v vrsticah #include. Vsi razen zadnjih dveh so potrebni za definiranje ukazov, ki sem jih uporabil v programu. Zadnja dva pa sta potrebna za pomozno funkcijo za resevanje sistema linearnih enacb.
Po deklaraciji spremenljivk sledi podajanje zelene vhodne datoteke in nato odpiranje vhodne ter izhodne datoteke (palpost.txt).
Branje iz vhodne datoteke poteka na osnovi kljucnih besed, ki jih program prebere in shrani v polje znakov key[ ]. Sledi serija if stavkov, ki dolocajo vrednosti spremenljivk. Branje poteka tako dolgo, dokler ni prebrani znak znak za konec datoteke (EOF - end of file). To mi omogoca vrstica
while(feof(data)==0)
Prvi del izracuna je izracun dolzin palic, ki jih program shrani v polje lSmembers], kjer je neznanka members stevilo palic. Dolzine palic potrebujem v nadaljevanju pri kreiranju togostne matrike k in pri izracunu sil v palicah.
Velikost togostne matrike je enaka produktu dimenzije in stevila vozlisc na kvadrat. Ker so doloceni cleni enaki 0, matriko k najprej inicializiram. S tem avtomatsko postavim clene matrike, ki jih program ne zajame na 0. Togostna matrika ima naslednjo shematsko obliko:
Matrika je kvadratna in simetricna glede na glavno diagonalo. Diagonalni cleni (ce je dimenzija = 2, so to cleni k11, k12, k21, k22 - prvi paket, k33, k34, k43, k44 - drugi paket, ... ,ce pa je dimenzija = 3, so to cleni k11, k12, k13, k21, k22, k23, k31, k32, k33 - prvi paket, k44, k45, k46, k54, k55, k56, k64, k65, k66 - drugi paket, ...) se izracunajo po naslednji formuli:
i=j 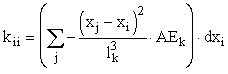
Formuli za preostali smeri (y in z) sta analogni, le da x nadomestimo z y oziroma z.
i&eq;j 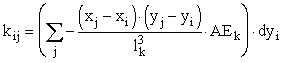
Za preostali kombinaciji x - z in y - z sta formuli analogni, le da namesto x in y vstavimo preostali kombinaciji. Ker je matrika glede na glavno os simetricna, nastopa v formuli za izracun kji namesto dyi dxi (oziroma preostali dve kombinaciji).
V formulah (4) in (5) imajo oznake naslednji pomen:
Preostali koeficienti imajo obliko:
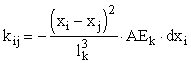
oziroma
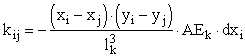
Oznake imajo enak pomen kot v formulah (5) in (4).
Vse te formule so izpeljane iz ravnotezne enacbe (2), s pomocjo izrazov za totalni diferencial dl in izrazov za sile v komponentni obliki (predloga: enacbe (4) in (5)).
Program deluje tako, da zapis diagonalnih cenov zagotovim s pomocjo spremenljivk c,c1,c2,k1,k2 in k3. Zapis diagonalnih in izven diagonalnih koeficientov togostne matrike poteka tako, da za dano vozlisce poisce vse palice, ki se stikajo v danem vozliscu in na podlagi ravnotezne enacbe zapise clene togostne matrike k.
Ker pomike nekaterih vozlisc ze poznamo, premiki v podporah so enaki 0, moramo transformirati togostno matriko tako, da bomo izracunali le pomike razlicne od 0, ker ne poznamo vrednosti reakcij v podporah - nepoznani koeficienti vektorja sil. Matriko transformiramo tako, da vrstice, ki vsebujejo pomike enake nic prestavimo na konec oziroma spravimo sistem linearnih enacb v obliko (10) - predloga.
Najprej program ugotovi katere vrstice je potrebno zamenjati in shrani te podatke v dvodimenzionalno polje vrstice[i][j], kjer je i indeks reakcije, j pa je 1 - za vrstico, ki jo je potrebno zamenjati in 2 - za vrstico s katero jo je potrebno zamenjati. Program gre od zadnje proti prvi reakciji. Zamenjava poteka tako, da zadnjo reakcijo postavi na zadnje mesto, predzadnjo na predzadnje...
Nato sledi zamenjava vrstic in stolpcev. Pred vsako zamenjavo program kontrolira pozicijo vrstice, ki jo hocem zamenjati, in ce je le-ta na pravem mestu se zamenjava ne izvede. Ko zamenjamo i-to vrstico, moramo zamenjati tudi i-ti stolpec, da ohranimo sistem linearnih enacb nespremenjen.
Potem sledi inicializacija matrike sil FSi] in zapis zunanjih obremenitev na ustrezna mesta. Ker je program transformiral togostno matriko, mora transformirati tudi matriko sil po istem principu.
Neznane pomike izracunam tako, da resim sistem enacb (14) v predlogi. To izvedem s pomocjo podprogramov za izracun linearnega sistema enacb ludcmp in lubksb. Vhodni podatki za omenjena pod- programa so togostna matrika k, velikost sistema dimenzija stevilo vozlisc - stevilo reakcij, permutacijska matrika indx (nima pomena za moj program; potreben za podprograma), kazalec y, ki tudi nima vpliva na moj program, in matriko sil F. Podprograma vrneta neznane pomike shranjene v matriki F.
Reakcije izracuna program po naslednji formuli:
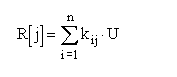
kjer je:
Sledi zamenjava pomikov na prvotna mesta v obratnem vrstnem redu kot prvotna zamenjava. S tem korakom dobim ponovno urejen prvotni vrstni red pomikov vozlisc (pomembno za izracun sil in zapis v izhodno datoteko).
Sile izracuna program po sledeci formuli:
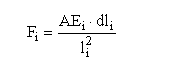
Preostanek programa je preprost izpis pomikov vozlisc, velikosti reakcij in velikosti sil v palicah na ekran (v istem vrstnem redu) ter zapis podatkov, ki so pomembni za postprocesor, v izhodno datoteko palpost.txt.

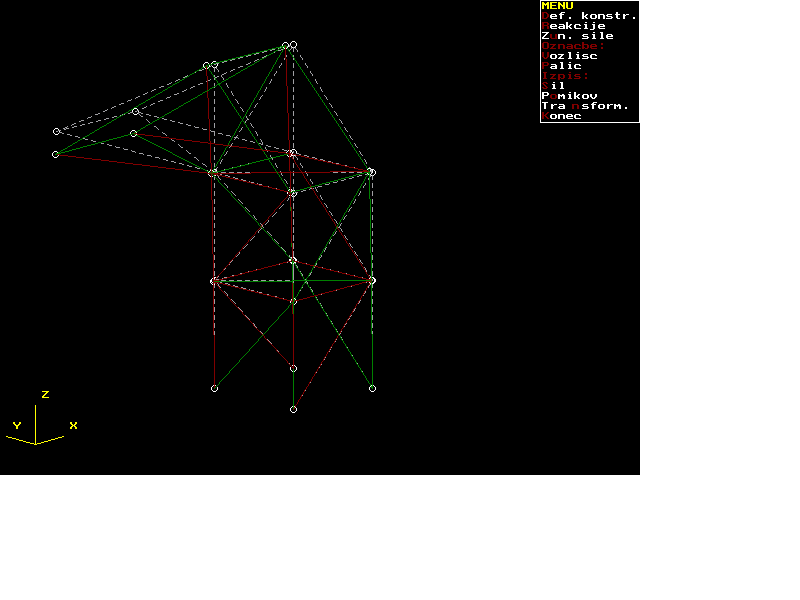
TESTNI PRIMER space joints 16 members 38 reactions 12 loads 2 coordinates 1 0.0 0.0 0.0 2 1000.0 0.0 0.0 3 1000.0 1000.0 0.0 4 0.0 1000.0 0.0 5 0.0 0.0 1000.0 6 1000.0 0.0 1000.0 7 1000.0 1000.0 1000.0 8 0.0 1000.0 1000.0 9 0.0 0.0 2000.0 10 1000.0 0.0 2000.0 11 1000.0 1000.0 2000.0 12 0.0 1000.0 2000.0 13 0.0 1000.0 3000.0 14 1000.0 1000.0 3000.0 15 1000.0 3000.0 2000.0 16 0.0 3000.0 2000.0 incidences 1 1 5 5e6 2 1 6 5e6 3 2 6 5e6 4 2 7 5e6 5 3 7 5e6 6 3 8 5e6 7 4 8 5e6 8 4 5 5e6 9 5 6 5e6 10 6 7 5e6 11 7 8 5e6 12 5 8 5e6 13 6 8 5e6 14 5 9 5e6 15 5 10 5e6 16 6 10 5e6 17 6 11 5e6 18 7 11 5e6 19 7 12 5e6 20 8 12 5e6 21 8 9 5e6 22 9 10 5e6 23 10 11 5e6 24 11 12 5e6 25 9 12 5e6 26 10 12 5e6 27 9 13 5e6 28 10 14 5e6 29 11 14 5e6 30 13 14 5e6 31 12 13 5e6 32 12 14 5e6 33 12 16 5e6 34 15 16 5e6 35 11 15 5e6 36 12 15 5e6 37 13 16 5e6 38 14 15 5e6 forces 15 0.0 0.0 -1000.0 16 0.0 0.0 -1000.0 supports 1 x 1 y 1 z 2 x 2 y 2 z 3 x 3 y 3 z 4 x 4 y 4 z solve
1 -0.0000 -0.0000 -0.0000 2 -0.0000 -0.0000 -0.0000 3 -0.0000 -0.0000 -0.0000 4 -0.0000 -0.0000 -0.0000 5 -0.3593 0.4205 0.4352 6 -0.3795 0.5847 0.3648 7 -0.6407 0.5795 -0.5648 8 -0.6205 0.4153 -0.6352 9 -0.6117 1.9630 0.8554 10 -0.6117 2.4169 0.7446 11 -1.3883 2.0370 -1.1446 12 -1.3883 1.5831 -1.2554 13 -0.8990 5.8050 -1.8554 14 -0.8990 6.0375 -1.7446 15 -0.6961 1.2370 -13.5816 16 -0.6961 0.7831 -14.1352
Prva stevilka pomeni zaporedno stevilko vozli�sc. Nato sledijo pomiki vozlisca v x,y in z smeri.
1 x 25.91 1 y 0.00 1 z -2149.99 2 x 0.00 2 y -25.91 2 z -1850.01 3 x -25.90 3 y 0.00 3 z 2850.01 4 x 0.00 4 y 25.91 4 z 3149.99
Prva stevilka je oznacba vozlisca. Drugi znak doloca smer delovanja podpore. Tretja stevilka je velikost reakcije v N.
Prva stevilka je zaporedna stevilka palice, druga pa velikost sile v N.
Sile v palicah
1 2175.89
2 -36.64
3 1824.10
4 36.64
5 -2824.10
6 -36.63
7 -3175.90
8 36.64
9 -100.90
10 -25.91
11 -100.90
12 -25.91
13 179.33
14 2100.90
15 142.70
16 1899.10
17 -142.69
18 -2899.10
19 142.70
20 -3100.90
21 -142.69
22 0.00
23 -1899.10
24 0.00
25 -1899.10
26 -142.70
27 2828.43
28 2828.42
29 -3000.00
30 0.00
31 -3000.00
32 -0.00
33 -2000.00
34 0.00
35 -2000.00
36 -0.00
37 2236.07
38 2236.07
Omejitve in pomankljivosti programa
Mozne izboljsave
Priloge