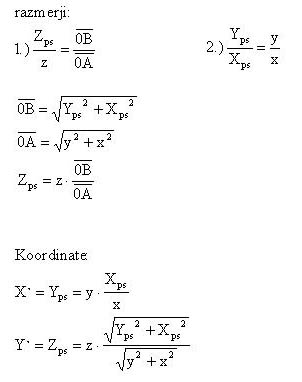Seminarska naloga:
Z - buffer (globinski pomnilnik)
Izdelal: Primož Pangeršič
Datum: 2. Sept. 1999
Mentor: mag. Leon Kos, dipl. ing.
Abstract:
On this page you can see an explanation of a Z buffer algorithm and a program that
shows us an example of use of a Z buffer algorithm. This example is made with a model of
sphere which is drawn on the screen. The model is drawn with small squares and triangles
on the top and on the dottom. Dimension of sphere and distance of the point of view can be
modified. There can be also modefied the delay of drawing. As an option you can also see a
drawing of a sphere without using a Z buffer algorithm.
Vsebina:
Potrebno je izdelati 3D primer za globinski pomnilnik Z buffer. Primer za 3D objekt je
tudi krogla popisana s kvadratnimi ploskvicami.
V tem poročilu je predstavljena logika Z buffer algoritma in njegova uporaba na
praktičnem primeru. Primer je prikazan s programom, ki nam izriše površino krogle.
Opisano je zaporedje operacij, ki potekajo od zagona programa pa do izrisa na zaslon.
Nazadnje so predstavljena navodila za uporabo programa.
Z buffer ali globinski pomnilnik je algoritem, ki nam, pri grafični predstavitvi,
pomaga urejati izris 3D objektov (vektorji, črte, poligoni…) na 2D zaslon tako, da ima
opazovalec občutek globine. Algoritem nam to omogoči tako, da se začnejo najprej
izrisovat objekti, ki so od gledalca najbolj oddaljeni. Izris pa se nadaljuje proti
objektu, ki je opazovalcu v 3D prostoru najbližji. Tako najbližji objekti vedno
prekrijejo bolj oddaljene in na zaslonu dobimo občutek globinske porazdelitve teh
objektov.
Torej najpomembneje je sortirati objekte po njihovi globini, jih transformirati v 2D
prostor in jih izrisati na zaslon v zaporedju od objekta z največjo globino (glede na
opazovalca) k objektu z najmanjšo globino. Pri tem se objekti prekrivajo in ob koncu
izrisa ne vidimo več objektov, ki so bili izrisani kot prvi.
Program za izris površine krogle z algoritmom globinskega pomnilnika je narejen v
programskem jeziku C++ oz. s pomočjo visual C++ (Microsoft Developer Studio).
V programu se najprej izvede delitev krogle z enačbo 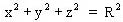 na poldnevnike in vzporednike. S
številom poldnevnikov in vzporednikov določimo tudi korak delitve. Razdelitev kota Fi
poteka od 0 do 2p (v X-Y ravnini), razdelitev po višini pa poteka s kotom Theta, ki
poteka od 0 do p (v smeri Z osi).
na poldnevnike in vzporednike. S
številom poldnevnikov in vzporednikov določimo tudi korak delitve. Razdelitev kota Fi
poteka od 0 do 2p (v X-Y ravnini), razdelitev po višini pa poteka s kotom Theta, ki
poteka od 0 do p (v smeri Z osi).
Vsaka dobljena točka je vektor (razred vektor):
x = m_cvPremik.GetX() +
m_dRadij*sin(Theta)*cos(Fi);
y = m_cvPremik.GetY() +
m_dRadij*sin(Theta)*sin(Fi);
z = m_cvPremik.GetZ() +
m_dRadij*cos(Theta);
in v razredu ploskev se vpisujejo po štirje vektorji, ki predstavljajo ploskev (glej
Sliko 1):
cpPloskev.SetBaseVector(cvBaseVector);
cpPloskev.SetRightVector(cvRightVector);
cpPloskev.SetTopRightVector(cvRightTopVector);
cpPloskev.SetTopVector(cvTopVector);
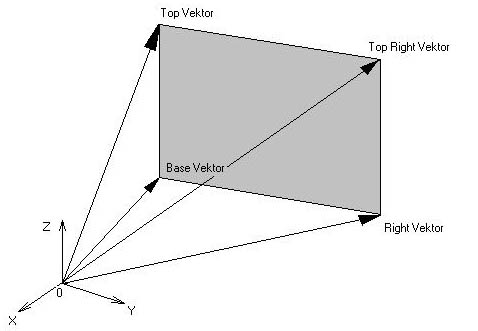
Slika 1 (definicija ploskve s 4 vektorji)
V prvi in zadnji vrsti (po višini) pa imamo namesto štirikotnikov trikotnike kar z
vektorji dosežemo tako, da sta:
- za zgornje trikotnike enaka zgornji in zgornji desni
vektor
- za spodnje trikotnike pa bazni in desni vektor.
Za pravilno zaporedje izrisa ploskvic in s tem zagotavljanje algoritma globinskega
pomnilnika, sortiram posamezne ploskvice po globini.
To se izvede tako, da program izračuna povprečno globinsko koordinato (t.j. X
koordinata)za štiri vektorje, ki določajo posamezno ploskev. Program torej izračuna X
koordinato težišča posamezne ploskvice. Potem sortira četvorke vektorjev (torej
ploskvice) glede na izračunano težišče (sort program npr. bubble sort). Najprej se
postavijo najbolj oddaljene, nadaljuje pa proti najmanj oddaljenem težišču.
Na novo sortirane ploskvice so še vedno zapisane s štirimi točkami, vsaka s po tremi
koordinatami. Za izris na zaslon pa jih je potrebno transformitat iz 3D v 2D prostor.
Za transformacijo se postavimo v neko točko iz katere gledamo na točke v prostoru (Point
Of View = POV). Izbral sem si izhodišče .... POV = (0,0,0).
Točke potem projeciramo na 2D zaslon. Velikost projekcije je odvisna od tega kje leži
točka, ki jo projeciramo. Če leži med POV in zaslonom, potem je slika povečana,
če pa leži za zaslonom potem je slika pomanjšana.
Algoritem za transformacijo je zelo enostaven.Glej sliko 2.
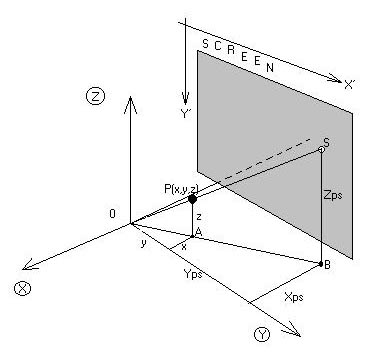
Slika 2 (projekcija 3D na 2D)
Prostorsko točko P(x,y,z) projeciram na zaslon in dobim projecirano točko S(x´,y´).
ALGORITEM TRANSFORMACIJE:
Poznani podatki: koordinate točke P, oddaljenost zaslona = Xps;
Izhajamo iz podobnih trikotnikov v katerih velja razmerje stranic:
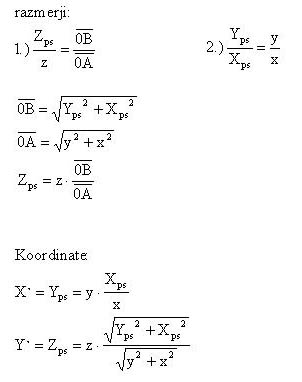
Posamezna ploskvica se nariše z linijo, ki poteka med transformiranimi vektorji
ploskvice (2D točkami), dokler se štirikotnik ne zaključi. Iste štiri točke hkrati
predstavljajo polygon, torej pobarvan štirikotnik (bele barve). Pri izrisu je to potrebno
zato, da prednja polovica krogle tako prekrije zadnjo polovico (dobimo občutek globine).
Risanje transformiranih ploskvic poteka v istem vrstnem redu, kot so sortirane po globini.
Hkrati se rišejo ploskvice z isto globino.
Program zaženemo s pomočjo ZBuffer.exe.
- Na zaslonu se prikaže dialog okno z imenom KROGLA.
- Na 2/3 okna je bela podlaga, kamor se izriše krogla. Krogla je izrisana s nastavljenimi
začetnimi vrednostmi parametrov.
- Na 1/3 okna pa so vrednost parametrov, ki jih lahko spreminjamo.

Slika 3 (Dialog okno KROGLA)
- Točka iz katere gledamo (POV) je v koordinatnem izhodišču.
Za začetni izris so nastavljeni naslednji parametri:
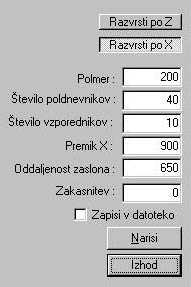
Slika 4 (parametri izrisa krogle)
- Globinsko koordinato nam predstavlja koordinata X (glej sliko 2) zato pomeni tipka Razvrsti
po X prikaz krogle z uporabo globinskega pomnilnika.
- Tipka Razvrsti po Z pa je dodana le zato, da vidimo kako se
izriše ista krogla brez sortiranja ploskvic po globini. Izriše se namreč po višini,
torej po Z koordinati v zaporedju, kot je bila diskretizirana sfera na začetku programa
(brez sortiranja).
- Edit Box Polmer predstavlja polmer izrisane krogle in je
nastavljen na 200
- Edit Box Število poldnevnikov predstavlja število delitev
obsega krogle - nastavljeno je na 40
- Edit Box Število vzporednikov predstavlja število delitev
višine krogle t.j. število plasti - nastavljeno na 10
(priporočeno razmerje vrednosti obeh zadnjih oken za lepo delitev in izris je približno
4:1)
- Edit Box Premik X predstavlja odmik središča krogle od
izhodišča po globinski koordinati X - nastavljen je na 900
- Edit Box Oddaljenost zaslona določa oddaljenost zaslona, na
katerega projeciramo sliko krogle, od izhodišča oz. gledišča - nastavljena je na 650
(s kombinacijo Premik X in Oddaljenost zaslona določam
velikost izrisane projekcije krogle)
- Edit Box Zakasnitev predstavlja ˝delay˝ oz.
zakasnitev pri risanju posameznih ploskvic v mili sekundah. Tako si lažje pogledamo
vrstni red izrisa posameznih ploskvic.
- Če označimo Check Box se shrani zapis
netransformiranih in transformiranih koordinat delitve sfere v txt datoteko. Zapišeta se
dve txt datoteki na mesto kjer se nahaja ZBuffer.exe z imenoma Stirikotniki2D.txt
in Stirikotniki3D.txt.
- S pritiskom na gumb Nariši se ponovno izriše krogla s
parametri, ki so trenutni vpisani Edit Box-e.
- S pritiskom na gumb Izhod pa zapustimo program.
Program normalno teče v Windows okolju. V primeru, da prekrijemo dialog okno KROGLA s
kakim drugim oknom, se izrisana krogla pobriše, vendar se ponovno nariše par sekund po
tem, ko naredimo okno KROGLA ponovno aktivno.
Z nastavljenimi parametri dobimo naslednjo obliko izrisane krogle:
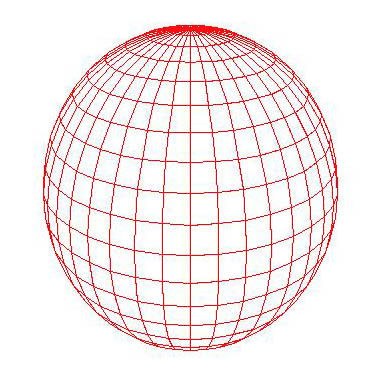
Slika 5 (Nastavljen izris krogle)
Položaj središča krogle je (900,0,400)
Oddaljenost zaslona je 650.
Če pritisnemo na tipko Razvrsti po Z se nam
izriše naslednja slika. Izriše se krogla po višini:
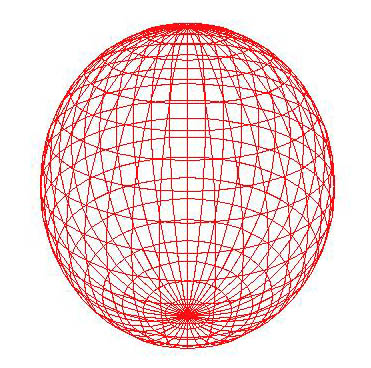
Slika 6 (Izris po višini, brez Z buffer-ja)
- 3D GAME programming with C++ / John De Goes / 1996
- Visual C++ programming
PROGRAM
Sedaj predlagam, da si s pritiskom na Download koda.zip
naložite exe program in kodo na disk ter ga preizkusite!
Primož Pangeršič
1999-9-2