Največkrat leže končni elementi konstrukcije poljubno v prostoru. Zato je potrebno pred nastavitvijo enačbe konstrukcije vse osnovne enačbe končnih elementov izraziti v skupnem (globalnem kooordinatnem sistemu).
Transformacijo končnih elementov iz lokalnih koordinatnih sistemov
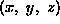v globalni koordinatni sistem 
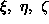. Vektor
v osnovnem koordinatnem sistemu
izrazimo v globalnem koordinatnem sistemu tako, da vsako komponento vektorja v osnovnem razstavimo v smerei koordinat glavnega koordinatnega sistema. Isto ležeče komponente združimo in dobimo
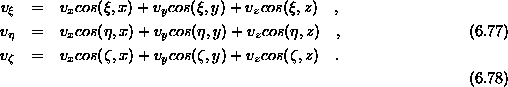
Kosinusi v enačbah so naklonski koti med lokalnimi in globalnim koordinatnim sistemom. Enačbo zapišemo krajše v matrični obliki
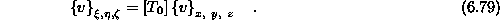
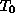je osnovna transformacijska matrika, ki transformira vektor iz
osnovnega v globalni koordinatni sistem in je v eksp[licitni obliki
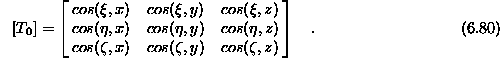
Matrika je nesingularna in simetrična zato zanjo velja matrična operacija
Poleg običajnih tro komponentnih vektorjev se uporabljajo v MKE tudi
posplošeni (generalizirani vektorji, enokolonske matrike).
Za transformacijo teh vektorjev se uporabljaja posplošena
transormacijska matrika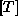 
oblike
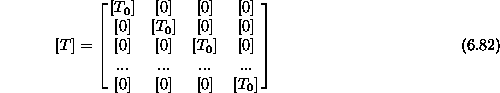
Tako bi bila transformacija posplošenega vektorja
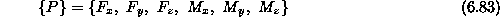
zapisana v matrični obliki
Posplosena transformacijska matrika je
zapisana v eksplicitni obliki
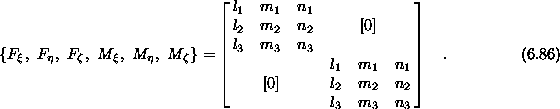
Kjer smo v enačbi označili z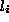 
, 
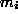in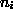 
naklonske kote med smermi
osi lokalnega in globalnega koordintnega sistema. Po množenju matrik dobimo
Z opisanimi pravili lahko sedaj naredimo transformacijo osnovne enačbe končnega elementa iz lokalnega v globalni koordinatni sistem. Za vozliščno silo in vozliščni pomik dobimo s transformacijo
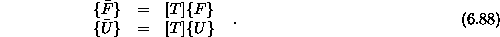
Če osnovno enačbo končnega elementa 
pomnožimo s
transformacijko matriko, dobimo
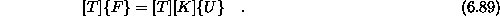
V enačbo vstavimo vektor vozliščnega pomika v globalnem koordinatnem sistemu
Tako da je
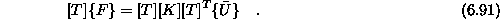
Preoblikujemo še levi del enačbe
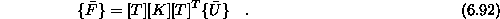
Enačba končnega elementa je s tem zapisana v globalnem koordinatnem sistemu. Z uvedbo transformirane togostne matrike
dobimo
Zadnja enačba zahteva veliko numeričnih operacij. V primeru, da so končni elementi že usmerjeni v smereh glavnega koordinatnega sistema, je potrebno izvesti veliko manj računskih operacij. Večinoma pa je to možno narediti le pri stenskih konstrukcijah.