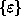 in
napetosti
in
napetosti 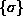 v odvisnosti od vozliščnega vektorja
v odvisnosti od vozliščnega vektorja 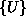 .
Tako pišemo
.
Tako pišemo
Z izbrano interpolacijsko funkcijo lahko nastavimo osnovno enačbo končnega
elementa. Izračunamo specifične deformacije 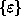 in
napetosti
in
napetosti 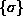 v odvisnosti od vozliščnega vektorja
v odvisnosti od vozliščnega vektorja 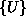 .
Tako pišemo
.
Tako pišemo
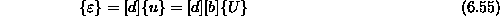
in če okrajšamo

ima enačba za specifične deformacije obliko
Enako naredimo z enačbo za specifične pomike
Z izpeljanima enačbama smo tako dobili povezavo deformacij in napetosti z z
vozliščnim vektorjem 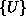 .
.
Vozliščni vektor pomikov dobimo iz osnovne enačbe končnega elementa, ki jo dobimo s pomočjo principa virtualnih pomikov.
Definiramo vozliščni vektor 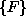 , ki ima enako število prostostnih
stopenj kakor vozliščni vektor. Elementi tega vektorja so komponente sil v
vozliščih končnega elementa. Za trikotni element stene bi bil vektor
, ki ima enako število prostostnih
stopenj kakor vozliščni vektor. Elementi tega vektorja so komponente sil v
vozliščih končnega elementa. Za trikotni element stene bi bil vektor
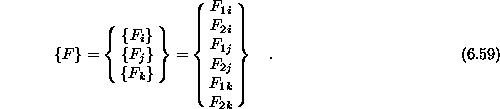
Virtualnim silam so prirejeni virtualni pomiki 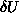 . Sedaj lahko
sapišemo virtualno delo zuanjih sil
. Sedaj lahko
sapišemo virtualno delo zuanjih sil

Virtualno delo notranjih sil pa je

Če v enačbo vstavimo enačbi ![]() in
in ![]() dobimo
dobimo
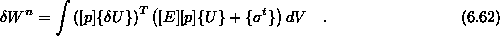
Po preureditvi je enačba
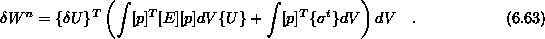
Z izenačitvijo izrazov za notranje in zunanje delo dobimo
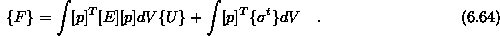
V zadnji enačbi označimo integrala

tako da dobimo osnovno enačbo končnega elemnta

in brez upoštevanja temperaturne obemenitve
Zadnja enačba podaja zvezo med vozliščnimi silami 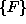 in vozliščnimi
pomiki
in vozliščnimi
pomiki 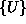 . Matriko
. Matriko 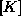 imenujemo togostna matrika in je specifična za
posamezen končen element. Z znano matriko
imenujemo togostna matrika in je specifična za
posamezen končen element. Z znano matriko 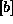 je možno izračunati vektor
vozliščnih pomikov. Konstrukcija ima e elementov in n vozlišč. Elementi
so povezani prek vozlišč v prvotno konstrukcijo. Z združitvijo e enačb
elementov dobimo enačbo konstrukcije. Ob upoštevanju robnih pogojev
(podpor in obremenitev) poiščemo iz dobljenega sistema linernih enačb
komponente vozliščnega vektorja.
je možno izračunati vektor
vozliščnih pomikov. Konstrukcija ima e elementov in n vozlišč. Elementi
so povezani prek vozlišč v prvotno konstrukcijo. Z združitvijo e enačb
elementov dobimo enačbo konstrukcije. Ob upoštevanju robnih pogojev
(podpor in obremenitev) poiščemo iz dobljenega sistema linernih enačb
komponente vozliščnega vektorja.
Prej omenjena togostna matrika 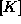 končnega elementa izračunamo samo enkrat
za vsak tip končnega elementa in je funkcija geometrije elemnta ter fizikalnih
konstant materiala.
Togostno matriko razvijemo naprej. Matrika
končnega elementa izračunamo samo enkrat
za vsak tip končnega elementa in je funkcija geometrije elemnta ter fizikalnih
konstant materiala.
Togostno matriko razvijemo naprej. Matrika 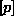 zapišemo še drugače
zapišemo še drugače
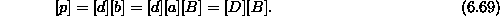
Kjer je

Enačbo ![]() sedaj zapišemo v obliki
sedaj zapišemo v obliki
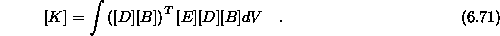
Matriko 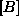 je možno izpostaviti saj vsebuje samo konstante elementa
(vozliščne koordinate).
je možno izpostaviti saj vsebuje samo konstante elementa
(vozliščne koordinate).
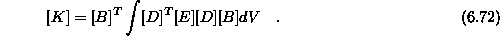
Enačbo še poenostavimo
kjer je
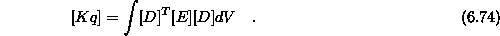
Matriko imenujemo posplošena ali generalizirana matrika končnega
elementa. Matrika ima poseben pomen. Matriki 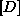 in
in 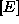 sta
neodvisni od položaja elementa v prostoru s tem pa imajo enaki
tipi končnih elementov enako posplošeno matriko, pod pogojem če
imajo enako matriko
sta
neodvisni od položaja elementa v prostoru s tem pa imajo enaki
tipi končnih elementov enako posplošeno matriko, pod pogojem če
imajo enako matriko 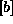 . Položaj posameznega vozlišča
elementa je zajet z matriko
. Položaj posameznega vozlišča
elementa je zajet z matriko

Togostna matrika se velikokrat računa po enačbi ![]() , predvsem pri
elementih višjega reda, ko bi bilo računanje matrike
, predvsem pri
elementih višjega reda, ko bi bilo računanje matrike 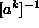 preveč
zapleteno.
preveč
zapleteno.