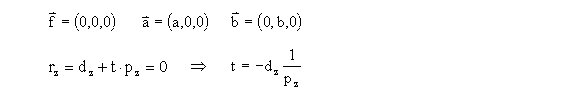Računalniško podprto konstruiranje - Vaje 1996/97 - 3.letnik KGS

Opisna Geometrija

Kazalo

Rešitev

Razred Premica

Razred Ravnina

Definicija naloge

Naloga je izdelava računalniškega programa, ki bi služil kot učni pripomoček za spoznavanje Opisne geometrije. Študentu bi predstavil 3D prostor z različnimi elementi, kot so osnovni geometrijski elementi: točka, premica in ravnina z različnimi liki ter osnovni prostorski elementi kot so prizma, piramida, stožec, valj in krogla.

Zahteve naloge:

Izdelajte razred (podprogram) računalniškega programa, ki bo omogočal predstavitev premice v 3D prostoru. Omogočeno mora biti določevanje premice:

z dvema točkama,

s točko in smernim vektorjem premice,

z znanima projekcijama premice na tlorisni in narisni ravnini.

Izvedene morajo biti metode za:

izris premice v 3D prostoru,

določitev in izris projekcij premice na tlorisni in narisni ravnini,

določitev in izris točk preboda tlorisne in narisne ravnine.

Izdelajte razred (podprogram), ki bo na osnovi znane premice in znane ravnine, ki sta določeni kot predstavnici svojega razreda, omogočil določitev točke preboda in njen izris v 3D prostoru ter na tlorisni in narisni ravnini.

Teoretične osnove

Določitev premice

Premica je v prostoru enolično določena z dvema različnima točkama, točko in smernim vektorjem ali s presekom dveh različnih ravnin. Za predstavitev premice se največkrat uporablja parametrična enačba premice:

Sl.1: Parametrična predstavitev premice

Krajevni vektor katerekoli točke na premici lahko dobimo s pomočjo znanih vektorjev r₀ in p ter ustrezno izbiro parametra t.

Določitev ravnine

Ravnina je v prostoru enolično določena s tremi različnimi točkami, s premico in točko izven te premice, s točko in normalnim vektorjem ravnine ali s točko in dvema nekolinearnima vektorjema. Tudi tu se največkrat uporablja parametrična oblika enačbe ravnine:

Sl.2: Parametrična predstavitev ravnine

Enotsko normalo ravnine lahko dobimo z vektorskim produktom vektorjev a in b in normiranjem:

Določitev točke preboda ravnine

Točko, kjer premica prebode ravnino, lahko izračunamo s pomočjo parametričnih enačb (1) in (2). Krajevni vektor točk na premici naj bo c, krajevni vektor točk na ravnini pa e:

Iščemo skupno točko premice in ravnine:

Sl.3: Prebod premice z ravnino

Ker imamo tri enačbe (za vsako koordinato posebej), lahko izračunamo neznane parametre t, u in w. Za ravnino xy dobimo:

Od tod dobimo komponente vektorja r :

V primeru da je p_z = 0, je premica vzporedna ravnini in prebodne točke ni.

Transformacija ravnine vzporedno ravnini xy

Poljubno ravnino lahko z vrtenjem okrog x- in y-osi zavrtimo vzporedno ravnini xy. Zaradi lažjega izvajanja predpostavimo, da se enotska normala poljubne ravnine nahaja v izhodišču in ima komponente n = (a, b, c). Z vrtenjem okrog x-osi za kot a in okrog y-osi za kot b usmerimo normalo v smer pozitivne z-osi:

Pozitivna kota označujeta pozitivno, negativna pa negativno smer vrtenja (pravilo desne roke).

Programski jezik Java

Java je novejši objektno orientirani programski jezik. Objekti v programskih jezikih so skupki spremenljivk in metod (funkcij), ki definirajo stanje in obnašanje objektov. Prednosti objektnega programiranja so v modularnosti --programsko kodo objekta lahko napišemo in popravljamo neodvisno od ostalih objektov, objekte lahko enostavno prenašamo med sistemi-- in skrivanju informacij --objekt ima javen vmesnik preko katerega lahko z njim komunicirajo drugi objekti, lahko pa ima tudi skrite informacije in metode, ki jih lahko spremeni neodvisno od ostalih objektov (Black Box princip)--.

V Javi je razred (class) neke vrste prototip objekta. Vsebuje spremenjljivke in metode, ki jih bodo imeli vsi objekti istega tipa. Nov objekt dobimo s klicanjem konstruktorja - metode v razredu, ki ima enak ime kot razred in ima nalogo ustvariti nov objekt tega tipa (alokacija spomina) in postaviti začetne vrednosti. Ko objekta ne potrebujemo več, je avtomatsko odstranjen iz spomina (garbage collected).

Razredi so urejeni hierarhično po načelu dedovanja (subclass, superclass). Podrazredi podedujejo spremenljivke in metode razreda, ki nam jih tako ni potrebno pisati znova, dodamo ali spremenimo pa jim lahko spremenljivke in metode specifične temu podrazredu. Na ta način so najbolj splošni razredi po hierarhiji najvišje, najbolj specializirani razredi pa najnižje. Sorodni razredi so združeni v pakete (packages), ki jih lahko nato uporabimo pri pisanju programov.

Java omogoča pisanje samostojnih programov ali pisanje applet-ov. Samostojni programi delujejo v svojem oknu ali ukazni vrstici, applet-i pa so vezani na datoteko HTML in jih lahko poganjamo v Java kompatibilnih pregledovalnikih.

Rešitev

Poleg razreda Premica, ki omogoča določitev in predstavitev premice v 3D prostoru, sem napisal oz. priredil še razrede osnovnih gradnikov geometrijskega prostora, ki sem jih nato uporabil pri pisanju razreda Premica. To so točka (razred Tocka), vektor (Vektor), ravnina (Ravnina) in tridimenzionalna transformacijska matrika (Matrix3D). Za predstavitev v prostoru sem napisal še razred Rhcs, ki postavi model koordinatnega prostora, in razred PremicaDemo, ki vse skupaj prikaže na zaslonu v obliki applet-a.

Dokumentacija razredov Premica, Ravnina, Rhcs, Tocka in Vektor je v obliki HTML datotek v poddirektoriju "docs".

Razred Premica
Konstruktorji

V razredu so definirani trije konstruktorji, ki omogočajo določevanje premice z dvema točkama (osnovni konstruktor), s točko in vektorjem in z znanimi projekcijami premice na koordinatnih ravninah. Slednja dva konstruktorja rezultirata s klicem prvega in mu posredujeta točki, ki ju izračunata iz sprejetih parametrov:
Premica(Tocka A, Vektor V, Rhcs cs) {
    this(A, new Tocka(A.x + V.x, A.y + V.y, A.z + V.z), cs);
}
Premica(float x1, float y1, float z1, 
	float x2, float y2, float z2, Rhcs cs) {
    this(new Tocka(x1,y1,z1), new Tocka(x2,y2,z2), cs);
}
Osnovni konstruktor določi krajevna vektorja obeh tock na premici in izračuna enotski smerni vektor premice. Nato kliče metodo, ki vrne polje vidnih prebodnih točk premice z ravninami mejnega kvadra:
ab = intersec(cs.rv);
V tem polju se nahajata samo dve različni točki, ki pa se lahko v polju ponavljata (vsaka največ trikrat). Do ponavljanja pride, kadar premica seka robove ali oglišča mejnega kvadra. Kadar premica seka samo dve ravnini, se v polju nahajata dve točki, ostala mesta v polju pa so prazna (null). Naslednji del kode konstruktorja poišče ti dve točki in jih shrani kot A in B:
for(int i = 0; i < ab.length; i++) {
    if(ab[i] != null) {
        A = new Tocka(ab[i]);
	break;
    }
}
for(int i = 0; i < ab.length; i++) {
    if(ab[i] != null && !A.equals(ab[i])) {
	B = new Tocka(ab[i]);
	break;
    }
}
Z naslednjimi klici konstruktor določi še prebodne točke premice s koordinatnimi ravninami:
XZ = intersec(cs.xz);
XY = intersec(cs.xy);
YZ = intersec(cs.yz);
Vseh teh pet prebodnih točk in trije vektorji so del vsakega objekta Premica (so člani razreda). Naloge konstruktorja so torej:

določiti krajevna vektorja obeh točk na premici,

določiti enotski smerni vektor premice,

poiskati prebodni točki premice z mejnim kvadrom,

poiskati prebodne toèke premice s koordinatnimi ravninami.

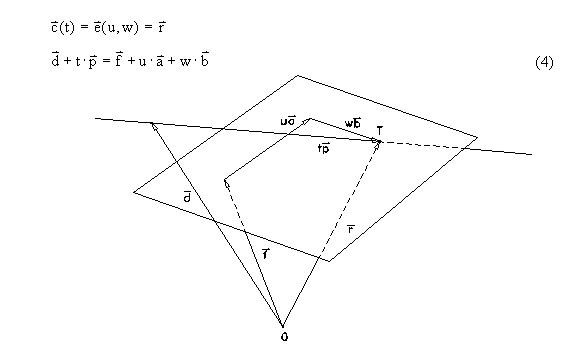
Metoda Tocka intersec(Ravnina rv)

Metoda izraèuna prebodno toèko premice s podano ravnino. Toèko vrne, èe se le-ta nahaja v vidnem delu ravnine t.j. znotraj poligona, ki definira ravnino na zaslonu. Oglišèa tega poligona se doloèijo ob konstruiranju nove ravnine. Prebodno toèko izraèuna s pomoèjo transformacije, ki transformira poljubno ravnino v ravnino xy. Isto transformacijo izvede tudi nad premico in izraèuna koordinate prebodne toèke na ravnini xy. Z inverzno transformacijo toèke nato vrne prebodno toèko premice s poljubno ravnino.
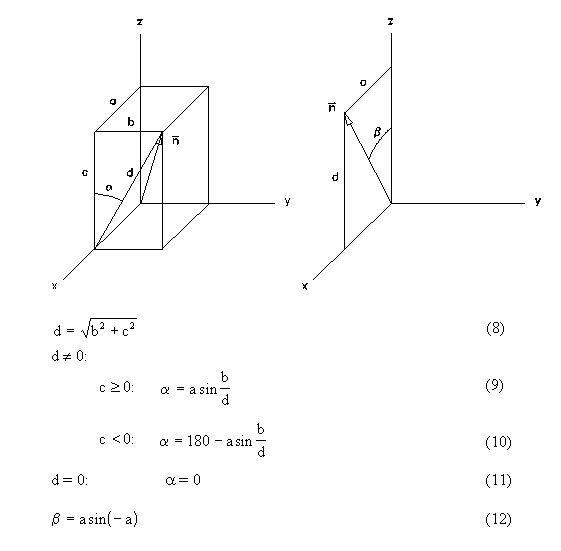
Transformacijsko matriko izraèuna s pomoèjo enotske normale podane ravnine, krajevnega vektorja prvega oglišèa poligona ravnine in z uporabo enaèb 8 ÷ 12:
d = Math.sqrt(rv.n.y * rv.n.y + rv.n.z * rv.n.z);
if(d == 0) alfa = 0;
else { alfa = (rv.n.z >= 0) ? 
              Math.asin(rv.n.y / d) * 180 / Math.PI :
              180 - Math.asin(rv.n.y / d) * 180 / Math.PI;
}
beta = Math.asin(-rv.n.x) * 180 / Math.PI;

// matrika za transformacijo ravnine rv v ravnino xy:
mat.unit();
mat.translate(-rv.V.x, -rv.V.y, -rv.V.z);
mat.xrot(alfa);
mat.yrot(beta);
Premico transformira s transformacijo krajevnih vektorjev toèk na premici:
tr1 = mat.transform(r1);
tr2 = mat.transform(r2);
Izraèun transformirane prebodne toèke (enaèbe 5, 6, 7):
Rz = tr2.z - tr1.z;
if( Rz < -1.e-5 || 1.e-5 < Rz ) { // premica ni vzporedna ravnini
    // izracun tocke preboda ravnine xy:
    tT.x = tr1.x - tr1.z * (tr2.x - tr1.x) / Rz;
    tT.y = tr1.y - tr1.z * (tr2.y - tr1.y) / Rz;
    tT.z = 0.f;
Matrika inverzne transformacije in vrnitev toèke, èe leži znotraj poligona:
// inverzna transformacija (xy -> rv):
mat.unit();
mat.yrot(-beta);
mat.xrot(-alfa);
mat.translate(rv.V.x, rv.V.y, rv.V.z);

// vrne tocko preboda, ce lezi v poligonu:
if(rv.inside(mat.transform(tT))) {
    return (mat.transform(tT));
}
V primeru da je premica vzporedna ravnini ali da prebodna toèka ni vidna, vrne metoda null.
Metoda Tocka[] intersec(Ravnina rv[])

Metoda je analogna prejšnji metodi s to razliko, da izraèuna prebodno toèko za vsako ravnino v polju in jo shrani v dva polja. V prvo polje shrani vsako toèko, v drugo pa le vidne toèke. Nezasedena mesta v polju ostanejo prazna (null). Metoda vrne polje vidnih prebodnih toèk, polje vseh izraèunanih toèk pa je definiramo kot èlan razreda.
Metoda void draw2D(Graphics g, int i, int j, ...)

Riše projekcijo premice znotraj mejnega kvadra na koordinatni ravnini xz in xy. Del projekcije, ki leži nad ravnino riše s polno, del, ki leži pod ravnino pa s èrtkano èrto. Pri doloèevanju kateri del leži nad ali pod ravnino uporabi prebodno toèko ravnine in prebodne toèke ravnin mejnega kvadra (polje vseh izraèunanih toèk iz prejšnje metode). S kombinacijo if stavkov in switch blokom doloèi med katerima toèkama mora narisati polno oz. èrtkano èrto, nato pa poklièe metodi full(..., Tocka t1, Tocka t2) in dash(..., Tocka t1, Tocka t2), ki èrto med projekcijama toèk dejansko narišeta. Barva èrt je doloèena z izbiro projekcijske ravnine.
Za pravilno risanje projekcij premice morajo biti mejne ravnine v polju v vrstnem redu kot je doloèen v razredu Rhcs.
Metoda void draw3D(Graphics g, int x0, int y0, ...)

Riše premico v 3D prostoru. Èe premica seka mejni kvader, jo nariše med toèkama A in B, drugaèe pa jo nariše "neskonèno". Neskonèno premico nariše s podaljšanjem premice v vsako stran od obeh toèk na premici. Pri tem uporabi enotski smerni vektor premice in enaèbo (1). Ta metoda riše tudi prebodne toèke na koordintnih ravninah (èe obstajajo in so vidne). Barva izrisane premice se poda kot argument metode.
Razred Ravnina
Konstruktorji

Konstruktorja v razredu sta dva:
Ravnina(Tocka P[])
Ravnina(Tocka P[], int stt)
Prvi doloèi ravnino s tremi toèkami, drugi pa z ravninskim poligonom v 3D prostoru. Oba konstruktorja doloèita krajevni vektor do prve toèke v polju in vektorja med prvo in drugo ter med prvo in tretjo toèko. Z vektorskim produktom slednjih dveh izraèunata normalo ravnine in jo normirata.
Naslednja naloga konstruktorja je doloèiti model ravnine kot polje oglišè ravninskega poligona v 3D prostoru. Drugi konstruktor samo kopira podano polje:
// model ravnine kot oglisca poligona:
op = new Tocka[stt];
System.arraycopy(P, 0, op, 0, stt);
Prvi konstruktor pa doda podanim toèkam še èetrto, ki jo izraèuna iz vsote vseh treh vektorjev. Tako dobi poligon obliko paralelograma:
// model ravnine kot oglisca poligona:
op = new Tocka[5];
op[0] = new Tocka(P[0]);
op[1] = new Tocka(P[1]);
op[2] = new Tocka(V1.x + V2.x + V.x, 
                  V1.y + V2.y + V.y,
                  V1.z + V2.z + V.z);
op[3] = new Tocka(P[2]);
op[4] = new Tocka(P[0]);
Zaradi lepše predstave bi moral biti poligon ravnine doloèen kot presek ravnine z mejnim kvadrom.
Za preverjanje ali prebodna toèka leži v poligonu ravnine, konstruktorja inicializirata še objekt Polygon (java.awt.Polygon). Ta ima v svojem razredu definirano metodo boolean inside(int x, int y), ki ugotovi ali toèka (x,y) leži v poligonu. Ker je objekt Polygon dvodimenzionalen, konstruktorja transformirata poligon ravnine v ravnino vzporedno ravnini xy po že znanih enaèbah:
// transformacija ravnine vzporedno ravnini xy:
d = Math.sqrt(rv.n.y * rv.n.y + rv.n.z * rv.n.z);
if(d == 0) alfa = 0;
else { alfa = (rv.n.z >= 0) ? 
              Math.asin(rv.n.y / d) * 180 / Math.PI :
              180 - Math.asin(rv.n.y / d) * 180 / Math.PI;
}
beta = Math.asin(-rv.n.x) * 180 / Math.PI;

// transformacijska matrika:
pmat.unit();
pmat.xrot(alfa);
pmat.yrot(beta);

// transformiran poligon:
tp = pmat.transform(op,5);

// inicializacija dvodim. poligona p:
for(int i = 0; i < 5; i++) {
    p.addPoint((int)tp[i].x, (int)tp[i].y);
}
Pri tem sta transformacijska matrika pmat in dvodimenzionalen poligon p èlana razreda in tako na voljo ostalim metodam.
Metoda boolean inside(Tocka T)

Metoda testira ali leži toèka znotraj poligona ravnine. Ker pri tem uporabi metodo boolean inside(int x, int y) razreda Polygon, mora toèko najprej transformirati z isto transformacijo kot jo je uporabil konstruktor pri inicializaciji dvodimenzionalnega poligona:

Tocka cht = pmat.transform(T);

Metoda inside(int, int) vrne false, èe toèka leži na robu poligona, zato je potrebno lego toèke malo prirediti:
int chx = (int)((cht.x < 0) ? (cht.x + 0.1f) :
                              (cht.x - 0.1f));
int chy = (int)((cht.y < 0) ? (cht.y + 0.1f) :
                              (cht.y - 0.1f));
Metoda vrne logièni izraz true, èe toèka leži v poligonu, drugaèe vrne false:

return p.inside(chx,chy);

Metoda void draw3D(Graphics g, int x0, int y0, ...)

Riše ravnino kot poligon v 3D prostoru. Barva ravnine je podana kot argument metode.
Sklep in opombe

Zahteva naloge je bila izdelati dva razreda, ki bi omogoèila predstavitev premice v prostoru in doloèitev prebodne toèke s poljubno ravnino. Ker bi slednji razred imel definirano le eno metodo, sem zaradi enostavnosti ta dva razreda združil v razred Premica.

Zaradi veèje modularnosti kode bi lahko metodo, ki doloèa prebodni toèki mejnega kvadra, prenesel v razred, ki doloèa model koordinatnega prostora, v tem primeru Rhcs. V tem primeru bi moral metodo spremeniti in podvojiti tako, da bi ena metoda vraèala prebodni toèki mejnega kvadra, druga pa bi vraèala polje prebodnih toèk z mejnimi ravninami.

Metoda, ki riše projekcije premice, je sicer dolga in nepregledna, vendar je to eden izmed hitrejših naèinov doloèitve projekcije, saj uporablja že izraèunane prebode mejnih ravnin, ki so nekakšen stranski rezultat doloèevanja preboda mejnega kvadra. Risanje neskonène premice, èe le-ta ne seka mejnega kvadra, je le eden izmed naèinov opozarjanja uporabnika, da je podal neprimerne podatke. Èe se podatki preverijo še preden se poklièe konstruktor Premice, se lahko ta del kode izpusti.

Pri pisanju razredov sem se trudil uporabiti èimveè že napisanih metod in razredov, ki so del Java okolja. Tako sem uporabil Polygon.inside(int, int) funkcijo za ugotavljanje lege prebodne toèke, ki uporablja sodo/liho metodo ugotavljanja notranjosti lika. Ker funkcija operira le s celimi števili in za toèko na robu poligona pravi da ni v poligonu, bi bilo potrebno kodo metode ustrezno spremeniti. Sam sem raje uporabil prirejanje lege kontrolirane toèke, kar sicer ni popolnoma zanesljivo, vendar zadovolji v veèini primerov.
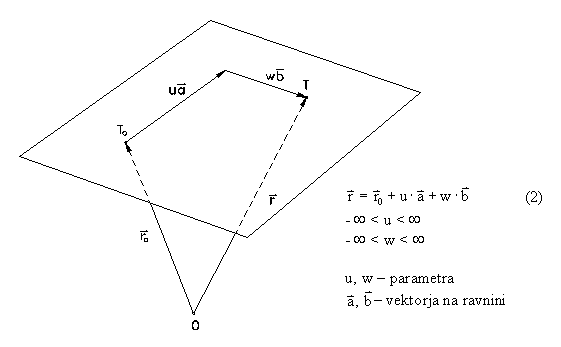
Drug naèin ugotavljanja lege prebodne toèke bi bil izraèun parametrov ravnine u in w po enaèbi (2). V tem primeru bi morala biti ravnina podana s tremi toèkami, ki bi doloèale vektorje r₀, a in b. Èe bi bila parametra u in w enaka ali med 0 in 1, bi toèka ležala v vidnem delu ravnine. Ta naèin pa ni uporaben, kadar je vidni del ravnine omejen s presekom ravnine z mejnim kvadrom ali kakim drugim telesom.

Razredi Tocka, Vektor in Rhcs so trivialni in jih na tem mestu nisem posebej opisal. Razrede PremicaDemo, DrawPad in DrawPad3D nisem opisal in dokumentiral, ker so bolj ali manj nepomembni in zaradi tega precej nedodelani.

Literatura

[1] D. Hearn, M.P. Baker. Computer graphics. Prentice Hall Inc., 1994.
[2] M. Campione, K. Walrath. The Java Tutorial. Addison-Wesley, 1997.

Matjaž Šubelj - 3.letnik KGS - 1996/97

Računalniško podprto konstruiranje - Vaje 1996/97 - 3.letnik KGS

Opisna Geometrija

Definicija naloge