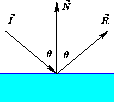
Zrcalna povrsina se zelo pogosto pojavlja v racunalniski grafiki, saj ucinkovito prikazuje zmoznosti upodabljanja z racunalnikom. Vecina povrsin ima tudi del zrcalnih lastnosti. Gladke povrsine, kot so kovine, stekla, ipd., odbijajo svetlobo pod istim kotom, kot je vpadni kot svetlobnega zarka. To dejstvo absolutno velja za popolno zrcalo, pri katerem je povrsina tako gladka, da se vsa svetloba odbije. Ce je povrsina prekrita s tanko plastjo, se del svetlobe lahko tudi absorbira v plasti. Primer take povrsine je navadno stekleno zrcalo iz stekla . Svetloba se tu deloma absorbira v steklu, vecji del pa se odbije. Podoben primer je tudi plast iz polirne paste, pri kateri se vecina svetlobe odbije ze na plasti, preostali delez pa se lomi in nato absorbira.

Dvosmerno odbojnostno funkcijo  lahko zapisemo kot kombinacijo dveh osnovnih
komponent: difuznega in zrcalnega odboj. Za zrcalni odboj je
znacilen odboj pod istim kotom, kar kaze slika
3.4. Prikazano lastnost zapisemo kot
lahko zapisemo kot kombinacijo dveh osnovnih
komponent: difuznega in zrcalnega odboj. Za zrcalni odboj je
znacilen odboj pod istim kotom, kar kaze slika
3.4. Prikazano lastnost zapisemo kot
Smer odboja zarka je smotrno formulirati v obliki, ki je primerna
za racunalnisko obdelavo. Odbiti zarek  zapisemo kot linearno kombinacijo vektorjev
zapisemo kot linearno kombinacijo vektorjev  in
in 
kjer sta  in
in  zaenkrat se neznani konstanti in ju
dolocimo z upostevanjem zakonitosti podani v enacbi
(3.8). V dveh dimenzijah je vpadni kot
zaenkrat se neznani konstanti in ju
dolocimo z upostevanjem zakonitosti podani v enacbi
(3.8). V dveh dimenzijah je vpadni kot 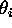 enak
odbitemu kotu
enak
odbitemu kotu  . S tem sta enaka tudi kosinusa
. S tem sta enaka tudi kosinusa
Enacbo (3.10) lahko zapisemo tudi s
skalarnim produktom in pri tem dolocimo konstanti  in
in
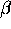 .
.
Ce je vektor nomale enotski  velja
velja  ; Lahko izberemo
; Lahko izberemo  in izrazimo konstanto
in izrazimo konstanto
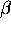 kot
kot
S tem dolocimo vektor odboja R iz enacbe (3.9) kot

ali ce uporabimo vektor luci  iz enacbe
(3.5)
iz enacbe
(3.5)

Ker je bilo ze v enacbi (3.11) predpostavljeno, da
so vsi vektorji enotski, se lahko pokaze, da je tudi  enotski [Gla91c] ob upostevanju lastnosti
(3.12) in
enotski [Gla91c] ob upostevanju lastnosti
(3.12) in  .
.
V praksi je vztrajanje na popolnem odboju svetlobe prevec stroga in
nerealna zahteva, saj obstajajo gladke povrsine, ki jih ne moremo
modelirati kot kombinacijo difuznega in zrcalnega odboja. To
bi pomenilo, da bi bili tockasti izvori svetlobe na takih
povrsinah vidni le v eni tocki. Iz izkusenj pa vemo, da so
tockasti izvori svetlobe vidni v doloceni blizini
kota zrcalnega odboja in da krozni odbleski na povrsini zvezno
pojemajo. Za pravilno porazdelitev lahko uporabimo ustrezno
empiricno porazdelitveno funkcijo. Bui-Toung Phong
[Pho75] je predlagal porazdelitev s funkcijo
 . Razlog izbora take porazdelitvene funkcije je tudi v
enostavnosti izracuna, saj lahko znova uporabimo skalarni produkt
med vektorjem odboja
. Razlog izbora take porazdelitvene funkcije je tudi v
enostavnosti izracuna, saj lahko znova uporabimo skalarni produkt
med vektorjem odboja  in vektorjem gledanja
in vektorjem gledanja  .
Intenziteta porazdeljenega zrcalnega odboja je modelirana kot
.
Intenziteta porazdeljenega zrcalnega odboja je modelirana kot
kar je graficno predstavljeno na sliki 3.5.

Z rastjo potence n se manjsa polje zrcalnega odboja.
Ce gre n proti neskoncnosti potem se enacba
(3.15) priblizuje zrcalnemu odboju.
Intenziteto odboja v smeri gledanja  dolocamo s
konstanto
dolocamo s
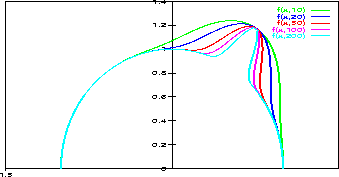
konstanto  . Graficna predstavitev za intenziteto difuzno in
zrcalno odbite svetlobe je podana za nekatere potence n na sliki
3.6. Videti je, da so uporabne vrednosti potence pri n =
10 ali vec.
. Graficna predstavitev za intenziteto difuzno in
zrcalno odbite svetlobe je podana za nekatere potence n na sliki
3.6. Videti je, da so uporabne vrednosti potence pri n =
10 ali vec.
 in
konstante n za primer difuznega in zrcalnega odboja
in
konstante n za primer difuznega in zrcalnega odboja
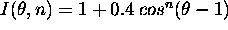
Enacba (3.15) kaze tudi to, da je pri kotu gledanja, ki je enak odbitemu kotu, funkcija intenzitete maksimalna. Ce uporabimo polovicni vektor
ki je povprecje vektorjev  in
in  , je v polozaju,
ko je
, je v polozaju,
ko je  vektor
vektor 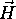 enak vektorju
enak vektorju  . Z
uporabo vektorja
. Z
uporabo vektorja  ni potrebno izracunavati
ni potrebno izracunavati 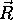 ,
ce uporabimo funcijsko odvisnost skalarnega produkta med
vektorjema
,
ce uporabimo funcijsko odvisnost skalarnega produkta med
vektorjema  in
in  . Enacbo (3.15)
uporabimo za vzor nove enacbe, pri kateri je potrebno uporabiti
dvakrat manjse potence n za isto porazdelitveno funkcijo.
. Enacbo (3.15)
uporabimo za vzor nove enacbe, pri kateri je potrebno uporabiti
dvakrat manjse potence n za isto porazdelitveno funkcijo.