 in
trikotnik T definiran s tremi nekolinearnimi ogljisci
in
trikotnik T definiran s tremi nekolinearnimi ogljisci  ,
,  in
in  .
.
Zahtevne povrsine se velikokrat v praksi raje aproksimirajo z mnozico trikotnikov ali mnozico planarnih konveksnih mnogokotnikov. Izracun presekov je lazji, napaka zaradi diskretizacije pa normalno ni opazna, ce uporabimo tehniko inkrementalnega sencenja in prilagodljivo delitev parametricnih povrsin z oceno ukrivljenosti v ploskvi.
Predpostavimo, da imamo zarek  in
trikotnik T definiran s tremi nekolinearnimi ogljisci
in
trikotnik T definiran s tremi nekolinearnimi ogljisci  ,
,  in
in  .
.
Povrsino P, ki vsebuje trikotnik T, zapisemo kot

kjer je  poljubno izbrana tocka na povrsini,
poljubno izbrana tocka na povrsini,  izhodiscna tocka, ki definira lego povrsine v
koordinatnem sistemu,
izhodiscna tocka, ki definira lego povrsine v
koordinatnem sistemu,  pa normala, ki doloca orientacijo
ravnine. Izhodiscna tocka je lahko katerokoli
ogljisce trikotnika.
pa normala, ki doloca orientacijo
ravnine. Izhodiscna tocka je lahko katerokoli
ogljisce trikotnika.
Normalo ravnine definirajo ogljisca trikotnika. Ravnina ima dve strani in s tem dve mozni usmerjenosti normal. Za dolocanje preseka izbor vrstnega reda ogljisc v vektorskem produktu ni pomemben:

Zarek  je na povrsini takrat, ko oddaljenost
je na povrsini takrat, ko oddaljenost  zadovoljuje enacbo
zadovoljuje enacbo
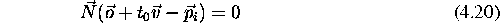
kar ob resitvi da

Ob dolocitvi presesica zarka z ravnino je potrebno
ugotoviti se ali se presecisce nahaja znotraj
trikotnika. Ogljisca trikotnika lahko uporabimo za nastavitev
enostavnega koordinatnega sistema  na ravnino P. Vsaka
tocka na ravnini je podana v tem koordinatnem sistemu kot:
na ravnino P. Vsaka
tocka na ravnini je podana v tem koordinatnem sistemu kot:

Tocka  se nahaja v trikotniku, ce
je:
se nahaja v trikotniku, ce
je:



Inverzne koordinate u in v dolocimo iz enacbe
(4.22) tako, da vektorsko enacbo napisemo
po komponentah. Ker so komponentne enacbe tri, neznanki pa dve, je
ena od enacb odvec. Osnovno pravilo pri odlocanju, katero
koordinato izlociti je, da izlocimo dominantno koordinato; to
je tista, ki ima v normali ravnine 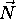 absolutno najvecjo
vrednost. Izberimo primer ravnine, ki ima najvecjo vrednost v
koordinati z normale
absolutno najvecjo
vrednost. Izberimo primer ravnine, ki ima najvecjo vrednost v
koordinati z normale  . Komponentni enacbi sta:
. Komponentni enacbi sta:

iz katerih lahko izrazimo polozaj tocke v koordinatnemu
sistemu ravnine  :
:

Po dolocitvi presecne tocke, je potrebno dolociti
pravilno stran ravnine, tako da velja enacba  . V dosedanjem obravnavanju se za normalo ni zahtevala enotska
dolzina, je pa obicajno potrebna pri osvetlitvenem modelu.
. V dosedanjem obravnavanju se za normalo ni zahtevala enotska
dolzina, je pa obicajno potrebna pri osvetlitvenem modelu.