Superquadrics[Barr, 1981, Loeffelmann and Groeller, 1994] are recent
geometric shapes with useful properties for computer
graphics. Superquadrics are an extension of the basic quadratic
surfaces defined as a spherical product of two parametric 2D curves,
resulting in a parametric 3D shape. Implicit equation for Piet-Hein
superelipsis is
and parametric set of equations is
where 
is the east-west or roundness/squareness
parameter.
Figure 2: Examples of superquadric elipsoids
Extending superelipses into 3D space, divides parametric
equations into family of superquadric elipsoids (fig. 2) and
superquadric toroids. For elipsoid family the parametric equations
(3) are defined as:
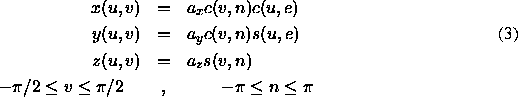
and similarly for superquadric toroids
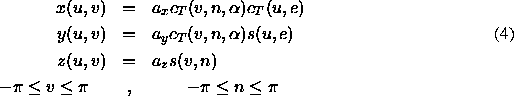
Sub functions used in the above equations (3 and
4) are defined as:
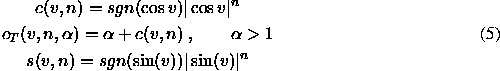
is the hole diameter used only for toroid shapes. 
are scale factors in each dimension. Parameter in
Eq.(2) is divided into two parameters e and n. It is
evident, that the equations (3) and (4) can
be combined together to form one set of equations.
Several other properties such as normal vectors, volume, mass, and inertia tensor can be easily derived for superquadrics. For detailed description of superquadric properties see [Barr, 1992].