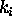
V poglavju 2 smo si ogledali osnovne zakonitosti svetlobe pri interakciji s povrsino. Za matematicno modeliranje razmer na povrsini je potrebno uvesti ustrezne poenostavitve, ki so obicajno kompromis med tocnostjo modela in potrebnim racunskim casom. Tako je zaradi zahtevnosti in potrebne kolicine podatkov, moc v programih z interaktivnim dostopom najti le najenostavnejse modele odboja. Taki modeli imajo obicajno vgrajen le en tockast vir svetlobe v neskoncnosti in Lambertov model difuznega odboja na povrsini.
Z zahtevami po realisticnih slikah raste tudi tocnost modelov in racunski cas, ki pa ga lahko s skupino in namenskimi procesorji zmanjsamo na zadovoljivo raven. Kljub temu, pa razmeram na povrsini ne smemo dati prevelike pomembnosti, saj so lahko za upodabljanje bistvenejsi drugi efekti realisticnosti, kot so teksture in moduliranje globine na povrsini.
Ugodno je tudi, ce lahko kontroliramo stopnjo realisticnosti. V modelirniku za CAD obicajno ne zelimo velike kvalitete izrisa ampak hitrost. Graficne delovne postaje imajo za interaktivno delo vgrajene posebne graficne procesorje, ki zmorejo v realnem casu osenciti nekaj tisoc mnogokotnikov. Zaradi vgrajene strojne opreme se lahko zgodi tudi paradoks, da modelirnik deluje hitreje z osencenimi, kot pa z zicnimi modeli.
Ko je potrebno izdelek predstaviti, pa se zahteva cimbolj verna predstavitev, ki najveckrat poudarja odbleske na gladkih povrsinah, teksture in fraktalna ozadja. Ce se zahteva se animacija, je lahko potreben cas za izracun vseh sekvenc tudi nekaj dni na enem samem procesorju.
Svetlobo lahko kolicinsko opredelimo na vec nacinov [Ash94,CW93]. Locimo predvsem dva pristopa k obravnavanju svetlobe: Radiometrija je znanost fizikalnega merjenja elektromagnetne energije; Fotometrija podaja oceno intenzitete svetlobe v enotah, ki upostevanjo obcutljivost cloveskega ocesa. Pomembno je predvsem to, da je edina razlika med fotometricno teorijo in teorijo sevanja le v enotah merjenja. V vecini graficnih sistemov so opticne kolicine podane s trojico barv: rdeca, zelena in modra (RGB).
Za enostavno kontrolo objektov v sceni lahko uporabimo model, ki
predpostavlja, da objekti sevajo svetlobo sami od sebe. Tako v barvnem
modelu RGB podamo svetilnosti za rdeco, zeleno in modro barvo.
Podobno je mozno uporabiti tudi druge barvne modele, pri katerih je
mozno zapisati linearno odvisnost intenzitete svetlobe in sevane
energije. Belo svetlobo je zato mozno obravnavati komponentno ali
celo monokromatsko[FvD90]. V tem primeru je
intenziteta svetlobe I kar enaka lastni svetilnosti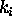 
Namesto samoosvetljenosti objekta lahko predpostavimo, da v prostoru
obstaja globalna osvetlitev, ki ni usmerjena in je zaradi tega
osvetljenost objektov z vseh strani enaka. Pri motnih povrsinah
lahko zapisemo podoben model osvetlitve, kjer se podaja
intenziteta osvetlitve ambienta 
in koeficient motnosti 
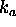
Koeficient difuznega odboja povrsine 
ima vrednosti med
nic in ena. Prednost modela (3.2) pred
(3.1) je tudi v tem, da lahko globalno
spreminjamo osvetlitev prostora. Poudariti pa je treba, da tako
enostavni modeli pri projekciji prikazejo le silhuete objektov,
kar je uporabno le za preizkus sirjenja primarnih zarkov v
metodi sledenja.
